【每日一题】用邮票贴满网格图

Tag

【二维前缀和】【二维差分】【矩阵】【2023-12-14】

---

题目来源

2132. 用邮票贴满网格图

---

题目解读

在 01 矩阵中，判断是否可以用给定尺寸的邮票将所有 0 位置都覆盖住，邮票之间可以重叠但是不能超出矩阵的的边缘。如果可以返回 true，否则返回 false。

---

解题思路

方法一：二维前缀和+二维差分

思路

我们贪心的进行覆盖，只要有足够大的空格（邮票尺寸那么大没被占据的）的地方，我们就用邮票来覆盖。记录空格被多少张邮票覆盖了，如果最后存在空格子没被覆盖，则返回 false，否则返回 true。

具体流程如下：

• 枚举邮票尺寸大小的矩形，需要使用二维前缀和判断枚举的区域是否没被占据；
• 记录空格被多少张邮票覆盖了，使用二维差分记录；
• 统计是否存在空格子没被覆盖，如是则返回 false，否则返回 true，使用二维差分还原。

二维前缀和

如何判断某个矩形区域可以覆盖邮票？只要该区域内没有被占据就可以，即一个矩形区域的元素和等于 0。为此，我们使用二维前缀和 $O(1)$ 的统计任意矩阵区域的元素和。

这里直接贴出代码，如果对二维前缀和内容不熟悉可以参考 一文讲清楚【前缀和】。

vector<vector<int>> preSum2d(m+1, vector<int>(n+1));
for (int i = 0; i < m; ++i) {
    for (int j = 0; j < n; ++j) {
        preSum2d[i+1][j+1] = preSum2d[i][j+1] + preSum2d[i+1][j] - preSum2d[i][j] + grid[i][j];
    }
}

二维差分

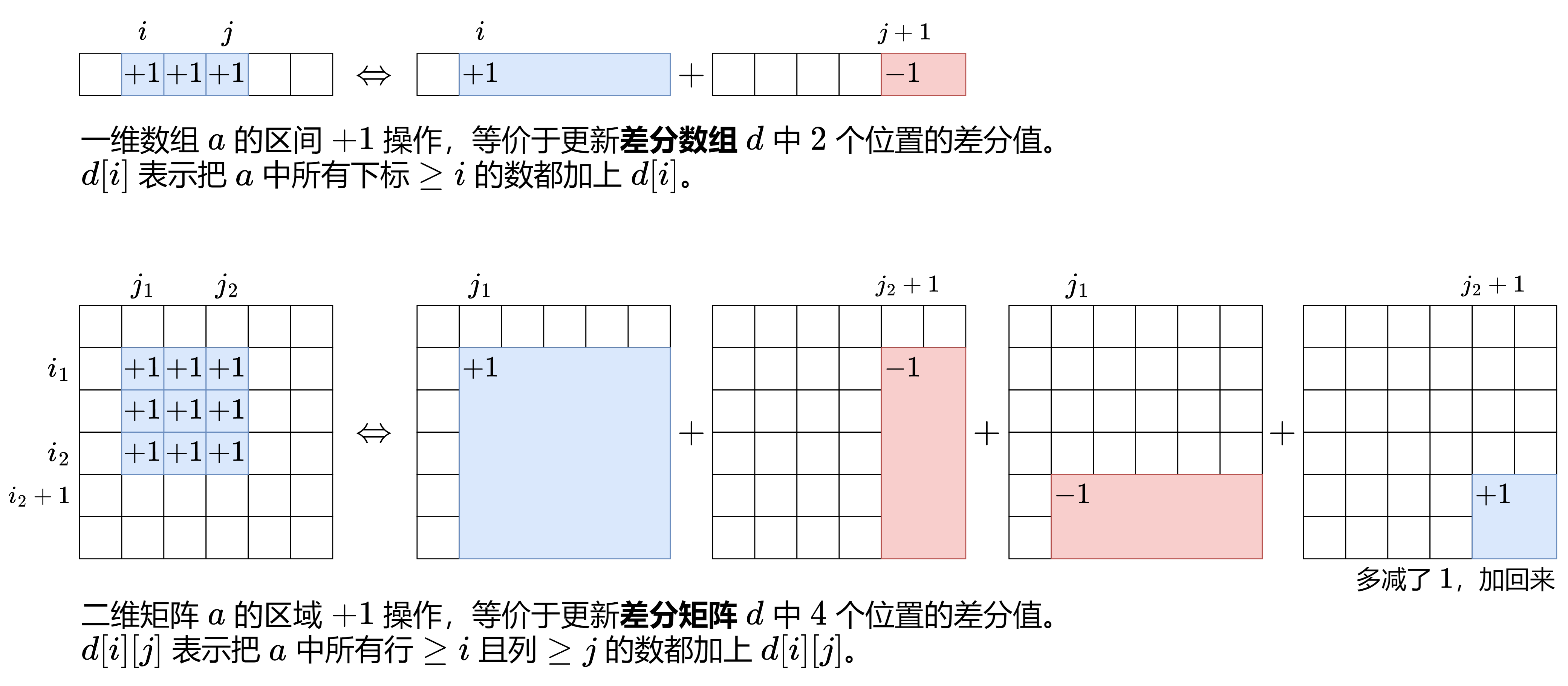
实现代码

class Solution {
public:
    bool possibleToStamp(vector<vector<int>>& grid, int stampHeight, int stampWidth) {
        int m = grid.size(), n = grid[0].size();
        vector<vector<int>> preSum2d(m+1, vector<int>(n+1));
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                preSum2d[i+1][j+1] = preSum2d[i][j+1] + preSum2d[i+1][j] - preSum2d[i][j] + grid[i][j];
            }
        }
        
        vector<vector<int>> diff(m+2, vector<int>(n+2));
        for (int i2 = stampHeight; i2 <= m; ++i2) {
            for (int j2 = stampWidth; j2 <= n; ++j2) {
                int i1 = i2 - stampHeight + 1;
                int j1 = j2 - stampWidth + 1;
                if (preSum2d[i2][j2] - preSum2d[i2][j1-1] - preSum2d[i1-1][j2] + preSum2d[i1-1][j1-1] == 0) {
                    diff[i1][j1] ++;
                    diff[i1][j2+1] --;
                    diff[i2+1][j1] --;
                    diff[i2+1][j2+1] ++;
                }
            }
        }

        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                diff[i+1][j+1] += diff[i+1][j] + diff[i][j+1] - diff[i][j];
                if (grid[i][j] == 0 && diff[i+1][j+1] == 0) {
                    return false;
                }
            }
        }
        return true;
    }
};

复杂度分析

时间复杂度：$O(mn)$，$m$ 和 $n$ 分别为数组 grid 的行数和列数。

空间复杂度：$O(mn)$。

---

写在最后

如果您发现文章有任何错误或者对文章有任何疑问，欢迎私信博主或者在评论区指出 💬💬💬。

如果大家有更优的时间、空间复杂度的方法，欢迎评论区交流。

最后，感谢您的阅读，如果有所收获的话可以给我点一个 👍 哦。