【PyTorch】权重衰减

1. 理论介绍

• 通过对模型过拟合的思考，人们希望能通过某种工具调整模型复杂度，使其达到一个合适的平衡位置。
• 权重衰减（又称$L_2$正则化）通过为损失函数添加惩罚项，用来惩罚权重的$L_2$范数，从而限制模型参数值，促使模型参数更加稀疏或更加集中，进而调整模型的复杂度，即：$$L(\mathbf{w},b)+\frac{\lambda }{2}\Vert \mathbf{w}{\Vert }^2$$其中$\lambda$为权重衰减的超参数。
• 权重衰减建立在以下假设上：权重的值取自均值为0的高斯分布。
• $L_p$范数：$$\Vert \mathbf{x}{\Vert }_p={\left(\sum _{i=1}^n{\left|x_i\right|}^p\right)}^{1/p}$$
  当$p=1$时称为$L_1$范数；当$p=2$时称为$L_2$范数。
  惩罚$L_1$范数会导致模型将权重集中在一小部分特征上， 而将其他权重清除为零， 这称为特征选择；惩罚$L_2$范数会导致模型在大量特征上均匀分布权重，使得模型对单个变量的观测误差更为稳定。
• 通常不建议对偏置进行正则化，因为偏置的取值并不像权值那样会随着训练过程而变化，因此对偏置进行正则化对于控制模型的复杂度影响较小；另外，对偏置进行正则化可能会导致对数据中的偏移进行过度拟合，而减弱了模型对其他特征的学习。

2. 实例解析

2.1. 实例描述

使用以下公式生成包含20个样本的小训练集和100个样本的测试集，并用线性网络进行拟合：$$y=0.05+\sum _{i=1}^{200}0.01x_i+?\text{?where?}?～\mathcal{N}(0,0.01^2).$$

2.2. 代码实现

2.2.1. 主要代码

optimizer = optim.SGD([
            {"params": net.weight,"weight_decay": weight_decay},
            {"params": net.bias}
            ], lr=lr)

2.2.2. 完整代码

import os
import torch
from torch import nn, optim
from torch.utils.data import TensorDataset, DataLoader
from tensorboardX import SummaryWriter
from rich.progress import track

def data_generator(w, b, num):
    """为线性模型生成数据"""
    X = torch.randn(num, len(w))
    y = torch.sum(X @ w, dim=1) + b
    y += torch.normal(0, 0.01, y.shape)
    return X, y.reshape(-1, 1)

def load_dataset(*tensors):
    """加载数据集"""
    dataset = TensorDataset(*tensors)
    return DataLoader(dataset, batch_size, shuffle=True)

def evaluate_loss(dataloader, net, criterion):
    """评估模型在指定数据集上的损失"""
    num_examples = 0
    loss_sum = 0.0
    with torch.no_grad():
        for X, y in dataloader:
            X, y = X.cuda(), y.cuda()
            loss = criterion(net(X), y)
            num_examples += y.shape[0]
            loss_sum += loss.sum()
        return loss_sum / num_examples


if __name__ == '__main__':
    # 全局参数设置
    lr = 0.003
    num_epochs = 100
    batch_size = 5

    # 创建记录器
    def log_dir():
        root = "runs"
        if not os.path.exists(root):
            os.mkdir(root)
        order = len(os.listdir(root)) + 1
        return f'{root}/exp{order}'
    writer = SummaryWriter(log_dir=log_dir())
    
    # 合成数据集
    num_inputs = 200
    n_train, n_test = 20, 100
    true_w, true_b = torch.ones((num_inputs, 1)) * 0.01, 0.05
    X, y = data_generator(true_w, true_b, n_train + n_test)

    # 加载数据集
    dataloader_train = load_dataset(X[:n_train], y[:n_train])
    dataloader_test = load_dataset(X[n_train:], y[n_train:])

    def loop(weight_decay):
        # 定义模型
        net = nn.Linear(num_inputs, 1).cuda()
        nn.init.normal_(net.weight)
        nn.init.constant_(net.bias, 0)
        criterion = nn.MSELoss(reduction='none')
        optimizer = optim.SGD([
            {"params": net.weight,"weight_decay": weight_decay},
            {"params": net.bias}
            ], lr=lr)

        # 训练循环
        for epoch in track(range(num_epochs), description=f'wd={weight_decay}'):
            for X, y in dataloader_train:
                X, y = X.cuda(), y.cuda()
                loss = criterion(net(X), y)
                optimizer.zero_grad()
                loss.mean().backward()
                optimizer.step()
            writer.add_scalars(f'wd={weight_decay}', {
                'train_loss': evaluate_loss(dataloader_train, net, criterion),
                'test_loss': evaluate_loss(dataloader_test, net, criterion),
            }, epoch)


    for weight_decay in [0, 3]:
        loop(weight_decay)
    writer.close()

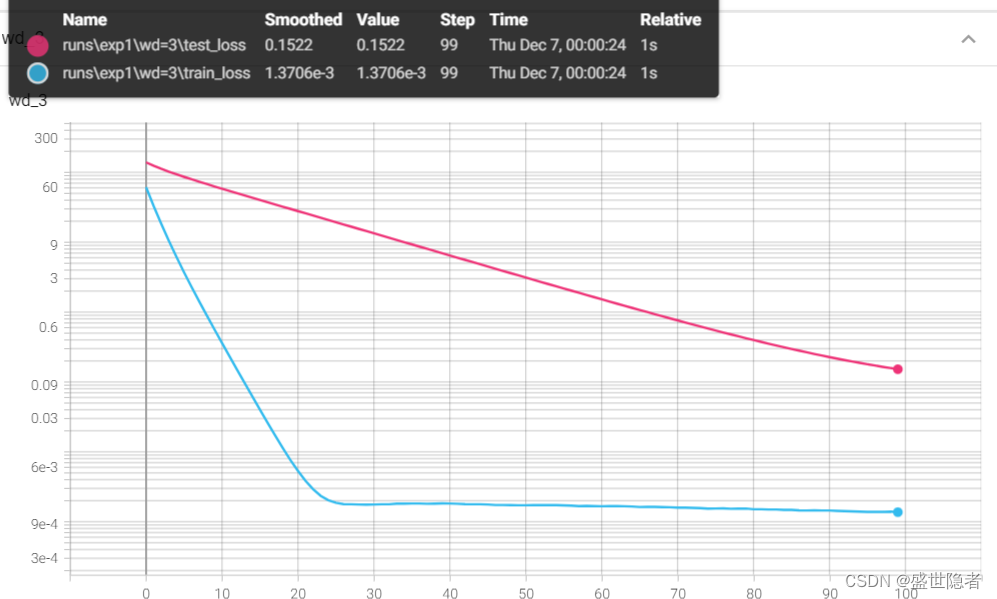
2.2.3. 输出结果

* weight_decay = 0

* weight_decay = 3