【算法】运用滑动窗口方法解决算法题（C++）

1. 滑动窗口 介绍

滑动窗口算法 通常用于解决字符串和数组相关的问题（如找子串、子数组）。

该算法的基本思想是维护一个固定大小的窗口，通过该窗口在字符串或数组上滑动，从而寻找符合条件的子串或子数组。在每次窗口滑动时，我们只需要对窗口内的元素进行简单的更新，以便快速得到新的结果。

---

2. 滑动窗口算法引入

209.长度最小的子数组

解法思路

• 解法一：暴力枚举
  • 两层循环，记录所有子数组的大小，最后得出满足条件的最小值
  • 时间开销大，时间复杂度O(n^2)

for (int i = 0; i < n; i++)
        int sum = 0;
        for (int j = i; j < n; j++)
            sum += nums[j];
            if (sum >= target)
            // ...

• 解法二：根据①单调性 使用 ②同向双指针

根据上图所示，而单调性+同向双指针的方法，我们称之为滑动窗口。
而滑动窗口算法解题一般分为以下步骤：

1. 初始化指针left，right
2. 控制元素入窗口（即开始移动右指针）
3. 条件判断（根据题目要求）
4. 出窗口（移动左指针）

• 需要注意的是，后三步的执行顺序和题目有关，并非固定的

代码

int minSubArrayLen(int target, vector<int>& nums) {
    // 滑动窗口
    int n = nums.size();
    int left = 0, right = 0;
    int sum = 0, len = INT_MAX;
    
    while(right < n)
    {
        sum += nums[right];   // 从前向后遍历数组 计算sum
        
        while(sum >= target) // 计算结果，更新sum
        {
            len = min(len, right - left + 1);
            sum -= nums[left++];
        }
    
        ++right;
    }
    
    // 如果没有满足条件的len，则返回0
    return len == INT_MAX ? 0 : len;
}

3. 使用滑动窗口解决算法题

3.无重复字符的最长子串

解法思路

• 解法一：暴力枚举+哈希表

  • 通过两层循环记录子串，并用哈希表记录所出现的字符，如果字符出现重复，则break此次循环
  • 时间复杂度O(n^2)

• 解法二：找规律，使用滑动窗口+哈希表
  

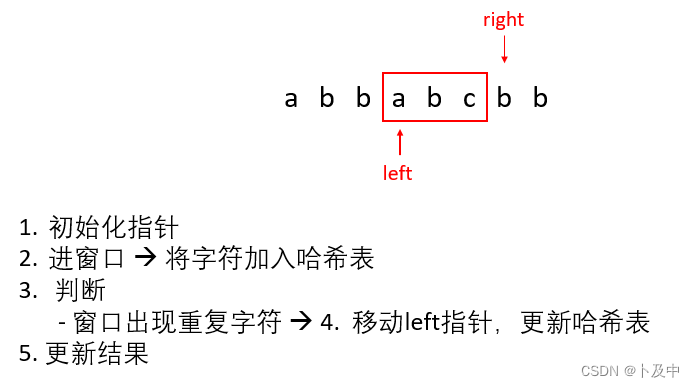
代码

int lengthOfLongestSubstring(string s) {
    int hash[128] = {0}; // 用数组模拟哈希表
    int ret = 0;
    for(int left = 0, right = 0; right < s.size(); ++right)
    {
        hash[s[right]]++; // 记录当前字符并++right

        while(hash[s[right]] > 1) // 遇到重复数，Left到重复数（前面的）的后一位

        {
            hash[s[left++]]--; 
        }

        ret = max(ret, right - left + 1);
    }

    return ret;
}

---

1004.最大连续1的个数III

解法思路

• 根据题目，我们可以将k个0翻转成1，由此我们可以将题目要求转化为：

  • 找到最长的子数组，其中0的个数 <= k，由此只需要根据条件找最长即可。

• 解法一：暴力枚举+zero计数器

  • zero计数器用于统计子数组中0的个数
  • 通过两层循环计算子数组
  • 时间复杂度O(n^2)

• 解法二：滑动窗口+zero计数器

  1. 初始化left、right指针
  2. 进窗口：每次循环末尾将right++
  3. 判断条件：根据当前值更新计数器
  4. 出窗口：当zerok，此时移动left指针，直到zero <= k
  5. 更新结果：每次循环尾部更新ret

代码

int longestOnes(vector<int>& nums, int k) {
    int left = 0, right = 0;
    int zero = 0, ret = 0; // 计数器，统计0的个数

    while(right < nums.size())
    {
        // 判断
        if(nums[right] == 0)    zero++;
        
        // 此时已经达到了最大能翻转的0的个数
        while(zero > k){
            if(nums[left] == 0)   zero--;
            left++;
        }
        
        // 更新结果
        ret = max(ret, right - left + 1);
        right++; // 移动窗口
    }

    return ret;
}

---

1658.将x减到0的最小操作数

解法思路

• 如果我们直接进行解题，对于这个数组，我们可以从左右两个方向移除元素，比较复杂，所以我们可以采用下面的方法
• 正难则反 ：将题目要求、思路逆转过来！
  • 题目要求 找到将x减到0 最小操作数
  • 我们只需找到数组中值为 n(数组长度) - x 的 最长子数组 即可
  • 由此我们可以想到使用滑动窗口解题

• 解法：滑动窗口
  1. 初始化指针和相关变量
  2. 进窗口：记录子串当前位置总和（tmp += nums[right]）
  3. 条件判断：当前子串和>target
     • 出窗口：tmp -= nums[left]，移动left指针
  4. 更新结果：当当前子串值tmp == target，更新结果ret
  5. 最后返回n - ret

代码

int minOperations(vector<int>& nums, int x) {
    // 思路：正难则反（将该题反过来思考）
    // 求和为target(sum-x)的最长子数组
    int sum = 0, n = nums.size();
    for(int num : nums) sum += num; // 计算数组总和 
    int target = sum - x, ret = -1;

    // x可能大于sum，此时return -1
    if(target < 0) return -1;

    // 解法：滑动窗口
    for(int left = 0, right = 0, tmp = 0; right < n; ++right)
    {
        tmp += nums[right]; // 进窗口

        while(tmp > target) // 判断
            tmp -= nums[left++]; // 出窗口
        if(tmp == target)
            ret = max(ret, right - left + 1); // 更新结果
    }

    // 由于我们是求的值为sum-x的最长子数组，按照题目要求返回n-ret
    return ret == -1 ? ret : n - ret;
}

---

904.水果成篮

解法思路

• 题意分析：即找到最长子数组，子数组要求只有两种元素

• 解法一：暴力枚举+哈希表

  • 暴力解法前面都有提到，类似的思路，这里跳过

• 解法二：滑动窗口+哈希表

  1. 进窗口：将right位置元素统计到哈希表中
  2. 条件判断：当kinds（元素种类）>2
     • 出窗口：将hash中left位置元素减去，移动left指针
  3. 更新结果：每次在循环尾部更新结果ret

代码

int totalFruit(vector<int>& fruits) {
    // 该题实际上可以理解为：求最长子数组，要求子数组只有两种类型的水果
    int left = 0, right = 0, ret = 0, n = fruits.size();
    // unordered_map<int, int> hash; // 哈希表统计某种类水果出现次数
    int hash[100001] = {0}; // 小优化，由于水果种类<=10^5，使用数组作为哈希表
    int kinds = 0;
    
    // 分析题目，解法为滑动窗口
    while(right < n)
    {
        if(hash[fruits[right]] == 0)    kinds++; // 使用变量判断水果种类
        hash[fruits[right]]++; // 进窗口
        
        while(kinds > 2) // 判断
        {
            hash[fruits[left]]--; // 出窗口
            if(hash[fruits[left]] == 0)
                kinds--;
            ++left;
        }
        
        ret = max(ret, right - left + 1); // 更新结果
        ++right;
    }
    
    return ret;
}

---

LCR015.找到字符串中所有字母异位词

解法思路

• 题意分析：题目要求找到所有的字母异位词，即找满足条件的子数组
• 解法：滑动窗口+哈希表
  1. 先用两个哈希表将s、p中字符的出现次数分别统计
     • hash1 存储p中各个元素的出现次数
     • hash2 记录当前滑动窗口内各个元素的出现次数
  2. 进窗口：将right位置元素统计到hash2中，并记录当前有效字符的个数count
  3. 条件判断：当滑动窗口（即当前统计的子串）过大，
     • 出窗口：移动left指针，并判断有效字符
  4. 更新结果：循环尾部，每次判断（有效字符个数==p长度），则将该索引位置(left)加入到ret中

代码

vector<int> findAnagrams(string s, string p) {
    int hash1[26] = {0}; // hash1 存储p中各个元素的出现次数
    for(char ch : p)    hash1[ch - 'a']++;
    int count = 0, pLen = p.size(); // count 记录有效字符的个数
    int hash2[26] = {0}; // 记录每次滑动窗口元素出现次数
    vector<int> ret;
    
    for(int left = 0, right = 0; right < s.size(); ++right)
    {
        char in = s[right];
        hash2[in - 'a']++; // 进窗口
        if(hash2[in - 'a'] <= hash1[in - 'a'])  count++; // 维护count，满足有效字符条件则++
        if(right - left + 1 > pLen) // 滑动窗口过大
        {
            char out = s[left++];
            if(hash2[out - 'a'] <= hash1[out - 'a']) count--;
            hash2[out - 'a']--;
        }

        if(count == pLen)   ret.push_back(left); // 更新结果
    }
    return ret;
}

---

30.串联所有单词的子串

解法思路

• 题意分析：我们需要找到所有串联子串在s中的开始索引
• 解法：滑动窗口+哈希表
  • 这道题与上一个题字母异位词 类似
  1. 如图所示，滑动窗口需执行len次，先嵌套一层for循环
  2. 内层循环执行滑动窗口操作↓：
     • hash1 ：用于统计 s 中当前窗口内各个字符串出现的次数
     • hash2 ：统计words中每个字符串的出现次数
  3. 进窗口：记录当前right位置的字符串in，如果满足条件则入hash1并更新count（有效字符串个数）
  4. 条件判断：如果窗口的大小是否超过了包含所有 words 字符串的最大可能长度
     • 出窗口：将hash中left位置字符串删去，移动left指针
  5. 更新结果：如果有效字符个数count == words大小，则将索引left加入到结果ret

代码

关于代码注释中提到的小优化：

// Similar to LCR 015. 找到字符串中所有字母异位词
vector<int> findSubstring(string s, vector<string>& words) {
    int len = words[0].size(), wSize = words.size();
    vector<int> ret; // 结果数组
    if(len > s.size())  return ret;

    unordered_map<string, int> hash2; // 统计 words 字符串次数
    for(string str : words)   hash2[str]++; // 统计次数

    for(int i = 0; i < len; ++i) // 执行len次
    {
        unordered_map<string, int> hash1; // 存储 s 中各字符串的次数
        for(int left = i, right = i, count = 0; right + len <= s.size(); right += len) // right每次跳过一个words中字符串大小
    // count 计算有效字符串的个数
        {
            string in = s.substr(right, len); // right位置字符串
            if(hash2.count(in) && ++hash1[in] <= hash2[in]) count++; // 进窗口 (hash2.count(in)，小优化如果hash2中没有in，就不执行，方括号会创建变量)
            // 判断
            if(right - left + 1 > len * wSize) // 出窗口 + 维护count
            {
                string out = s.substr(left, len);
                if(hash2.count(out) && hash1[out] <= hash2[out]) count--;
                hash1[out]--;
                left += len;
            }

            if(count == wSize) ret.push_back(left);
        }
    }   
    return ret;
}

---

76.最小覆盖子串

解法思路

• 该题与上一题串联思路相似，重点在于条件判断
• 题意分析：题目要求返回字符串s的最小子串，该子串包含字符串t的所有字符
• 解法：滑动窗口+哈希表
  • 先初始化相关变量和哈希表
    • hash1：统计t所有字符
    • hash2：记录s中当前窗口字符的出现次数
  1. 进窗口：若right位置字符满足条件，则放入hash2中，并更新count(有效字符的个数)
  2. 条件判断：根据下图，当count == kinds时：
     
  • 更新结果：如果此时滑动窗口大小 < minLen(当前记录的最短子串长)，则更新结果
  • 出窗口：将left位置字符从hash2中减去，判断是否是满足条件的字符，如果是则count–

代码

string minWindow(string s, string t) {
    int hash1[128] = {0}; // 统计t的字符
    int hash2[128] = {0}; // 统计字符串
    int kinds = 0; // 统计t中 字符的种类
    for(char ch : t) 
        if(hash1[ch]++ == 0) kinds++;

    int minLen = INT_MAX, begin = -1; // 最后要用的结果，最小子串的长度和起始位置
    for(int left = 0, right = 0, count = 0; right < s.size(); ++right)
    {
        char in = s[right];// 进窗口
        if(++hash2[in] == hash1[in]) count++;    // 当t中的字符次数与当前in的次数一致时，更新count

        // 判断
        while(count == kinds)
        {
            if(right - left + 1 < minLen)
            {
                minLen = right - left + 1; // 更新结果
                begin = left; // 记录待返回字符串的起始索引
            }

            char out = s[left++]; // 出窗口
            if(hash2[out]-- == hash1[out]) count--;
        }
    }
    return begin == -1 ? "" : s.substr(begin, minLen);
}