蓝桥杯备赛系列 高精度 acwing版

? ? ? ? ? ? ? ? ? ? ? ? ? ? ????????? ? 前言

hello，好久不见。元旦玩过后该收心了，我也倒计时一下蓝桥杯考试时间，大家一起复习，一起登顶。今天讲解高精度算法。

这个算法其实是给学c++同学讲的，因为python自带高精度所以不需要，且我讲到所有内容都是c++版本，今年就要报考c++，今年学好了Java可以上Java内容。

不多bb了上正文

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 正文

?????????先介绍一下为什么要用高精度。

1. int：通常，int?类型的大小是依赖于特定平台的，常见的有 16 位（2 字节）、32 位（4 字节）和 64 位（8 字节）等。在某些平台上，int?可能只有 16 位，能够存储的最大值是 32767；而在其他平台上，int?可能有 32 位或 64 位，能够存储的最大值分别是 2147483647 和 9223372036854775807。
2. long long：long long?类型通常至少有 64 位，并且能够存储的最大值是 9223372036854775807。实际上，long long?的大小和能够存储的最大值也是依赖于特定平台和编译器的。

所以由此看来如果输入的数过大int 和longlong类型都会爆掉，那我要是硬使用

会怎么样呢，下面这个照片给大家展示一下。

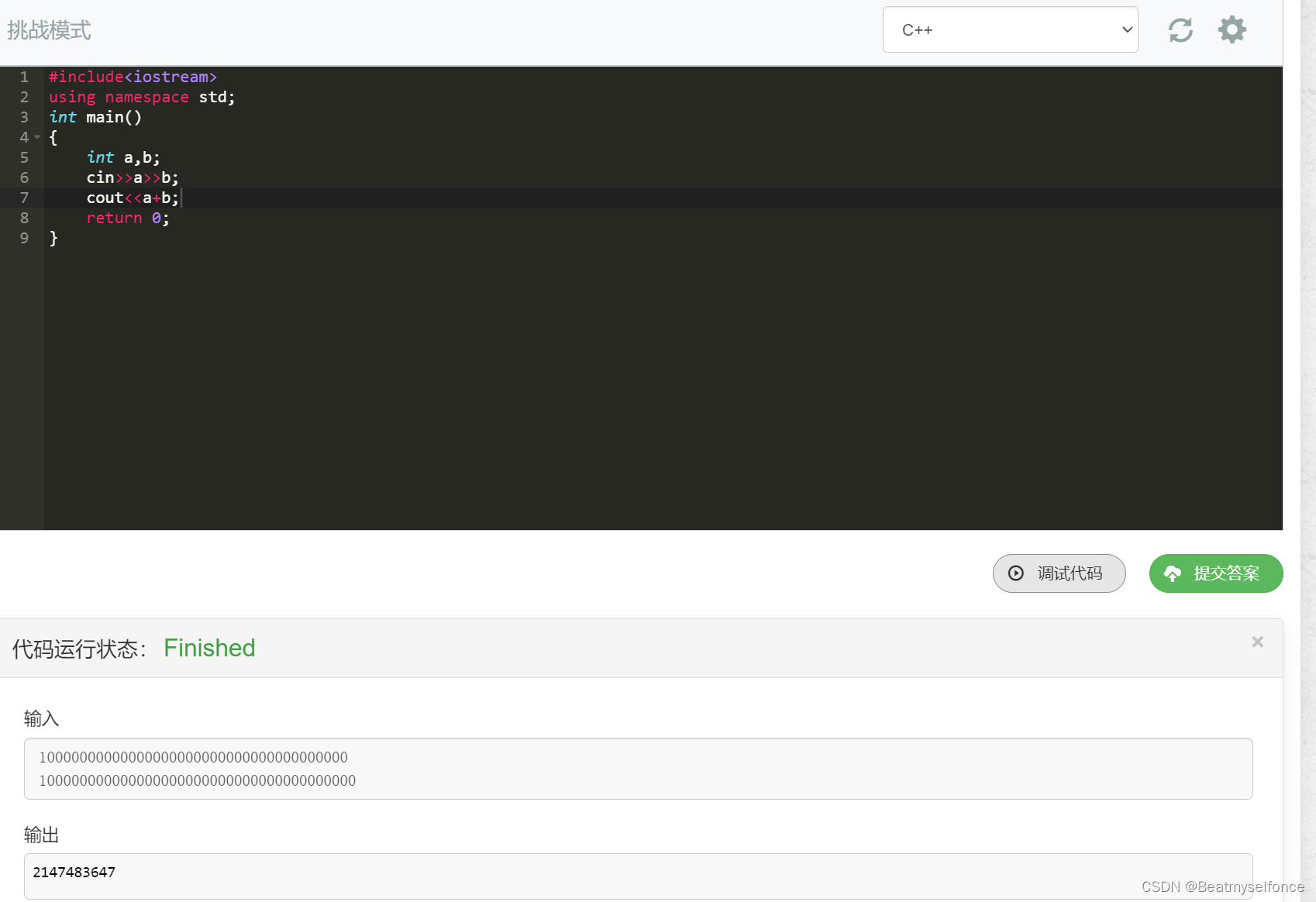
?很明显是不行的，所以要引入高精度这个算法。

高精度如何存数字呢，很明显就是数组。

高精度加法
主要思想：用字符数组进行接收数字，将数字逐一逆序存储到数组中，对应位置依次相加。
在此之前，我们回忆一下小学加法的做法：
1.对应位置相加
2.逢十进一

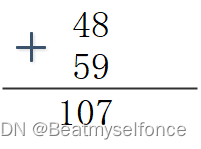
（1）8+9=17,逢十进一，17%10得到个位存储的数字为7。
（2）4+5+1=10,逢十进一，10%10得到个位存储的数字为0。
（3）两个数字百位都没有数字了，所以百位存储的数字就为1。
（4）得到答案107。

高精度加法步骤：
(1):字符数组存储大数字
(2):逆序插入整形数组
(3):对应位置数字相加，并进行%10运算存储到数组中，逢十进一
(4):将数组数字逆序输出

#include <iostream>
#include <vector>

using namespace std;

vector<int> add(vector<int> &A, vector<int> &B)
{
    if (A.size() < B.size()) return add(B, A);

    vector<int> C;
    int t = 0;
    for (int i = 0; i < A.size(); i ++ )
    {
        t += A[i];
        if (i < B.size()) t += B[i];
        C.push_back(t % 10);//t=a+b eg：t=12,t%10=2 push back  放入c的最后一位
        t /= 10;//eg：x=12，x/10=1
    }

    if (t) C.push_back(t);
    return C;
}

int main()
{
    string a, b;
    vector<int> A, B;
    cin >> a >> b;
    for (int i = a.size() - 1; i >= 0; i -- ) A.push_back(a[i] - '0');//读入的话是把小数放入a[0]以此类推
    for (int i = b.size() - 1; i >= 0; i -- ) B.push_back(b[i] - '0');

    auto C = add(A, B);//auto相当于一种定义类型，这里计算机可以直接判断定义类型

    for (int i = C.size() - 1; i >= 0; i -- ) cout << C[i];//输出的话我们习惯于把高位放在第一个跟读入的方式相反
    cout << endl;

    return 0;
}

(1)设置一个足够大的数N，用于标识数组的长度
(2)创建两个字符数组用于存储高精度数字
(3)创建整形数组
(4)(5)求两个高精度数字的位数
(6)(7)将两个高精度数字逆序存储到整形数组中
(8)存储两个数字中长度更长的
(9)计算新数组的长度
(10)(11)将两个数字对应位置进行相加
(12)将相加得到的数字%10存储到数组中
(13)判断是否需要进1
(14)判断最后是否还需要进1
(15)逆序打印
?

高精度减法
主要思想：用字符数组进行接收数字，将数字逐一逆序存储到数组中，对应位置依次相减。做法和高精度加法类似。
小学减法的做法：
1.对应位置相减，不够相减就向后一位借1

高精度减法步骤：
(1):字符数组存储大数字
(2):逆序插入整形数组
(3):对应位置数字相减，并判断当前所在位的被减数是否需要借1
(4):将数组数字逆序打印
?

#include <iostream>
#include <vector>

using namespace std;

bool cmp(vector<int> &A, vector<int> &B)
{
    if (A.size() != B.size()) return A.size() > B.size();

    for (int i = A.size() - 1; i >= 0; i -- )
        if (A[i] != B[i])
            return A[i] > B[i];

    return true;
}

vector<int> sub(vector<int> &A, vector<int> &B)
{
    vector<int> C;
    for (int i = 0, t = 0; i < A.size(); i ++ )
    {
        t = A[i] - t;
        if (i < B.size()) t -= B[i];
        C.push_back((t + 10) % 10);
        if (t < 0) t = 1;
        else t = 0;
    }

    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

int main()
{
    string a, b;
    vector<int> A, B;
    cin >> a >> b;
    for (int i = a.size() - 1; i >= 0; i -- ) A.push_back(a[i] - '0');
    for (int i = b.size() - 1; i >= 0; i -- ) B.push_back(b[i] - '0');

    vector<int> C;

    if (cmp(A, B)) C = sub(A, B);
    else C = sub(B, A), cout << '-';

    for (int i = C.size() - 1; i >= 0; i -- ) cout << C[i];
    cout << endl;

    return 0;
}

(1)设置一个足够大的数N，用于标识数组的长度
(2)创建两个字符数组，用于接收高精度数字
(3)创建两个整形数组，用于逆序存储高精度数字
(4)接收相减的结果
(5)将大数字逆序插入到整形数组中
(6)比较两个高精度数字的长度，用于后面消除前导0
(7)比较两个高精度数字的大小
(8)模拟减法竖式运算
(9)对应位置数字相减
(10)将相减得到的结果插入到数组中
(11)判断是否需要向后一位借1
(12)去除前导0
(13)逆序打印结果

高精度乘法

主要思想:依旧是模拟小学的乘法运算，使用字符数组存储大数字，再逆序存储到整形数组中。
小学乘法的做法:
1.对应位置相乘
2.对相乘的结果%10加到后一位

这里我们进行乘法的模拟运算：

?

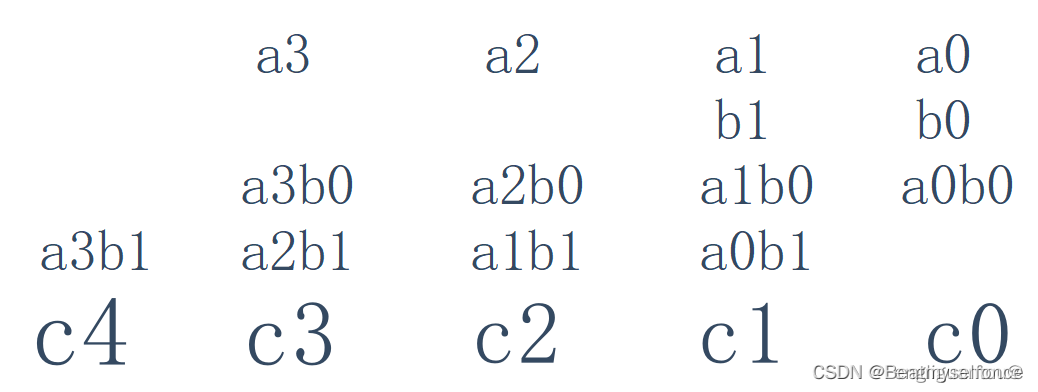
通过该图我们发现：
a0b0对应C1的位置
a1b0对应C1的位置
a2b0对应C2的位置
a3b0对应C3的位置
a0b1对应C1的位置
a1b1对应C2的位置
a2b1对应C3的位置
a3b1对应C4的位置
由此可以归纳出来一个规律
C[i+j]=a[i]*a[j]
由此也可得出进位等于C[i+j+1]

高精度乘法的步骤：
(1):字符数组存储大数字
(2):逆序插入整形数组
(3):对应位置数字相乘，相乘结果进行%10运算，并加到后一位上。
(4):将数组数字逆序打印
?

#include <iostream>
#include <vector>

using namespace std;


vector<int> mul(vector<int> &A, int b)
{
    vector<int> C;

    int t = 0;
    for (int i = 0; i < A.size() || t; i ++ )
    {
        if (i < A.size()) t += A[i] * b;
        C.push_back(t % 10);
        t /= 10;
    }

    while (C.size() > 1 && C.back() == 0) C.pop_back();//考虑b=0的情况的，如果b!=0就不用加

    return C;
}


int main()
{
    string a;
    int b;

    cin >> a >> b;

    vector<int> A;
    for (int i = a.size() - 1; i >= 0; i -- ) A.push_back(a[i] - '0');

    auto C = mul(A, b);

    for (int i = C.size() - 1; i >= 0; i -- ) printf("%d", C[i]);

    return 0;
}

(1)设置一个足够大的数N，用于标识数组的长度。
(2)创建两个字符数组用于存储高精度数字。
(3)创建整形数组。
(4)将数字逆序插入数组中
(5)对所得结果%10进行进位操作
(6)相乘得到的结果需要进行%10才能存储到数组中
(7)去除前导0
(8)逆序打印数字
?

高精度除法

主要思想:依旧是模拟小学的除法运算，使用字符数组存储大数字，再存储到整形数组中。（这里插入到数组中，不是逆序插入！）

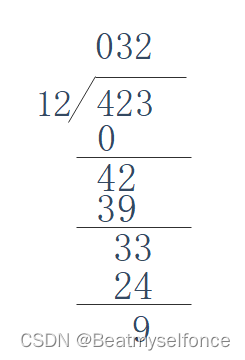
(1)4/12不够除，所以第一位商0
(2)42/12商3余3
(3)33/12商2余9
所以答案就为32余9
这里的过程为：
4/12，不够除
410+12=42 ，42/12=3，这位余下了一个3
310+3==33 ， 33/12=2，被除数每一位都走完，除法结束。余数为0
可以得到规律：
前一位的余数*10+当前位的数字/除数=商

高精度除法步骤：
(1):字符数组存储大数字
(2):正序插入整形数组
(3):计算上一位的余数*10+当前位的数字/除数的结果
(4):计算当前位的余数
(5):将数组数字逆序打印
?

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

vector<int> div(vector<int> &A, int b, int &r)
{
    vector<int> C;
    r = 0;
    for (int i = A.size() - 1; i >= 0; i -- )
    {
        r = r * 10 + A[i];
        C.push_back(r / b);
        r %= b;
    }
    reverse(C.begin(), C.end());
    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

int main()
{
    string a;
    vector<int> A;

    int B;
    cin >> a >> B;
    for (int i = a.size() - 1; i >= 0; i -- ) A.push_back(a[i] - '0');

    int r;
    auto C = div(A, B, r);

    for (int i = C.size() - 1; i >= 0; i -- ) cout << C[i];

    cout << endl << r << endl;

    return 0;
}

(1)创建一个足够大的N为数组分配空间
(2)创建一个字符串数组用于存储大数字
(3)(4)创建两个整形数组，一个用于存储大数字，一个用于存储结果
(5)存储低精度数字
(6)将大数字按正常顺序存储数组中
(7)因为是第一位，没有上一位，所以余数t一开始设置为0
(8)当前位的数字加上上一位的余数*10,再除以除数
(9)计算当前位的余数
(10)去除前导0
(11)顺序打印结果
?