演员-评论家算法：多智能体强化学习核心框架

演员-评论家算法

• • • 演员-评论家算法：策略梯度算法 + DQN 算法
    • • 演员-评论家的协作流程
      • 演员：策略梯度算法
      • • 计算智能体策略预期奖励的梯度
        • • 公式分解
          • 时间流程拆解
        • 通过采样方法近似估计梯度
        • • 公式拆解
          • 时间流程拆解
        • 改进策略
        • • 设置基线：适用于减小方差、加速训练效率
          • 归因分配 Credit Assignment：
      • 评论家：DQN算法

?

---

演员-评论家算法：策略梯度算法 + DQN 算法

演员-评论家算法 在多智能体强化学习中常作为核心框架，使得每个智能体可以独立学习自己的策略，同时评估其他智能体的策略对自身决策的影响。

1. 演员-评论家算法分成两半，一半是演员，另一半是评论家。

   • 演员：这一半基于概率分布，策略梯度算法。它有一个神经网络，可以根据行为的概率，选出行为。

   • 评论家：这一半基于行为价值，DQN 算法。它有一个神经网络，可以根据行为的价值，进行打分。

   将概率分布和行为价值的方法相结合：

   • 由基于概率分布的策略网络，在连续场景中选出行为
   • 由基于行为价值的价值网络，给行为提供实时反馈
   • 组合后，能在连续场景下，得到实时反馈

2. 策略和值函数的结合：

   • 演员直接学习策略，而评论家估计价值函数。这种结合提供了策略梯度的优势（直接优化策略）和值函数优势（减少方差，加速学习）。
   • 如果用边想边干比喻，想就是求价值函数，干就是求策略函数。
   • 好的“想”（价值函数的准确估计）会导致更好的“干”（更有效的策略），而有效的“干”（实践中的行动）又会回过头来改进“想”的过程（更准确的价值估计）。

3. 策略更新：演员根据评论家提供的反馈来更新其策略。这通常通过策略梯度方法实现，其中梯度由评论家的估计值指导。

4. 减少方差：使用评论家可以减少策略梯度估计的方差，因为评论家提供了对预期奖励的更准确估计。

5. 持续学习：演员-评论家方法适用于持续的任务，其中智能体需要不断地做出决策并从经验中学习。

6. 探索和利用：如同其他强化学习算法，演员-评论家也需要在探索（尝试新的、可能更好的行为）和利用（使用已知的最佳行为）之间找到平衡。

演员-评论家的协作流程

你是一个演员，你的任务是在舞台上表演。

你可以尝试不同的表演方式，比如不同的台词、动作或表情。

• 尝试新动作：在强化学习中，动作就是在特定情况下应该采取的行为

现在，有一个评论家坐在观众席上，观看你的表演并给出反馈。

• 评价表演：评论家的工作是评价演员的表演。在算法中，评论家评价演员选择特定动作的好坏，并预测这些动作的结果。

演员表演：

• 演员在给定的场景中尝试一个动作。
• 这个动作可以是基于以前的经验，或者尝试一些新的东西。

评论家评价：

• 评论家观察演员的动作，并根据动作的潜在好处或坏处给出评分。
• 这个评分基于演员的动作可能带来的奖励。

演员学习和调整：

• 基于评论家的评价，演员了解哪些动作是好的，哪些是不太好的。
• 演员使用这个反馈来调整其未来的表演策略，以便在类似情况下作出更好的动作选择。

重复并改进：

• 这个过程重复进行。每次演员尝试新动作，评论家给出评价，然后演员根据这些评价来改进。
• 随着时间的推移，演员通过这种反馈学习如何在不同情况下做出最佳的动作选择。

话分俩头，先说一下策略梯度算法，再说DQN算法。

演员：策略梯度算法

策略梯度算法，用于优化策略。

• 在强化学习中，策略定义了一个智能体在给定状态下选择动作的方式

• 策略梯度算法的目的是通过调整策略参数来最大化累积奖励

• 核心思想是直接对策略进行参数化，并使用梯度上升（或下降）方法来更新策略参数

比如在走迷宫或打败敌人。

策略梯度算法就是一种方法，用来教会这个智能体如何做出最好的决策。

策略 指的是智能体在特定情况下应该做什么动作的规则。

例如，在看到敌人时，策略可能是攻击或逃跑。

策略梯度算法的目标是找到最优的策略，即让智能体在游戏中获得最高分数或奖励的策略。

工作方式是这样的：

1. 尝试和错误：智能体开始时可能不知道什么是最好的行动，所以它会尝试不同的动作来看哪些动作能得到更好的结果。

2. 评估和学习：每次智能体做出决策并看到结果后，策略梯度算法会评估这个决策是好是坏，并根据这个评估来调整智能体的策略。如果某个动作导致了好结果（比如赢得更多分数），算法就会倾向于让智能体未来更多地采取这个动作。

3. 梯度上升：这个调整过程类似于数学中的梯度上升方法。算法计算每个动作如何影响最终奖励的概率，并调整策略以增加获得更高奖励的动作的概率。

4. 持续改进：随着智能体不断尝试和学习，它的策略会逐渐改进，最终找到一种策略，使它能在游戏中获得最高的奖励。

这个公式是策略梯度算法中的核心数学表达，涉及到了如何更新一个智能体的策略来获得更好的表现。让我们逐步分解这个公式，以便于更容易理解。

计算智能体策略预期奖励的梯度

$\begin{array}{rl}{\bar{R}}_{\theta }& =\sum _{\tau }R(\tau )p_{\theta }(\tau )={\mathbb{E}}_{r～p_{\theta }(\tau )}[R(\tau )]\\ & \\ p_{\theta }\left({\tau }^n\right)& =\sum _{t=1}^{r_n}{p}_{\theta }\left(a_t^n\mid s_t^n\right)\\ & \\ \theta & \leftarrow \theta +\eta ?{\bar{R}}_{\theta }\end{array}$

公式分解

1. 第一行：$({\bar{R}}_{\theta }={\sum }_{\tau }R(\tau )p_{\theta }(\tau )={\mathbb{E}}_{r～p_{\theta }(\tau )}[R(\tau )])$

   • ${\bar{R}}_{\theta }$：这代表智能体在当前策略（由参数 $\theta$ 决定）下的预期奖励。
   • ${\sum }_{\tau }R(\tau )p_{\theta }(\tau )$：这个部分计算所有可能的行动序列 $(\tau )$的总奖励 $R(\tau )$，考虑到每个序列发生的概率 $p_{\theta }(\tau )$。
   • ${\mathbb{E}}_{r～p_{\theta }(\tau )}[R(\tau )]$：这是预期奖励的另一种表达方式，它是说，按照当前策略，我们预期能获得的平均奖励。

2. 第二行：$(p_{\theta }({\tau }^n)={\sum }_{t=1}^{r_n}{p}_{\theta }(a_t^n|s_t^n)$

   • $p_{\theta }({\tau }^n)$：这表示第 (n) 个行动序列 ${\tau }^n$ 发生的概率。
   • ${\sum }_{t=1}^{r_n}{p}_{\theta }(a_t^n|s_t^n)$：这个公式计算一个特定行动序列中每个动作发生的概率之和。换句话说，它把每个时间点的动作发生概率相乘，以得到整个序列的概率。

3. 第三行：$\theta \leftarrow \theta +\eta ?{\bar{R}}_{\theta }$

   • $\theta \leftarrow \theta +\eta ?{\bar{R}}_{\theta }$：这是参数更新的步骤。这里，$\theta$ 是策略参数，$\eta$ 是学习率（一种决定参数更新步长的值），$?{\bar{R}}_{\theta }$ 是预期奖励关于策略参数的梯度。

时间流程拆解

1. 开始状态：智能体有一组初始策略参数 $\theta$。

2. 行动和观察：智能体根据当前策略做出一系列行动，并观察到结果（奖励和新状态）。

3. 计算预期奖励：使用第一行的公式计算在当前策略下的预期奖励。

4. 计算概率：根据第二行的公式计算行动序列的概率。

5. 更新策略参数：使用第三行的更新规则来调整策略参数。梯度 $?{\bar{R}}_{\theta }$ 指向能提高预期奖励的方向，策略参数 $\theta$ 则沿着这个方向更新。

6. 重复过程：用新的策略参数 $\theta$ 重复上述过程，直到策略达到满意的效果或满足其他停止条件。

这个公式描述了智能体如何通过学习和经验逐渐改进其行为策略，目的是为了最大化其在给定任务中获得的总奖励。

通过不断地尝试、评估结果。
?

通过采样方法近似估计梯度

$\begin{array}{rl}& ?{\bar{R}}_{\theta }=\sum _{\tau }R(\tau )?p_{\theta }(\tau )\\ & =\sum _{\tau }R(\tau )p_{\theta }(\tau )\frac{?p_{\theta }(\tau )}{p_{\theta }(\tau )}\\ & =\sum _{\tau }R(\tau )p_{\theta }(\tau )?\log p_{\theta }(\tau )\\ & ={\mathbb{E}}_{\tau ～{\rho }_{\theta }(\tau )}\left[R(\tau )?\log p_{\theta }(\tau )\right]\\ & \approx \frac{1}{N}\sum _{n=1}^{N}R\left({\tau }^n\right)?\log p_{\theta }\left({\tau }^n\right)\\ & =\frac{1}{N}\sum _{n=1}^N\sum _{t=1}^{T_n}R\left({\tau }^n\right)?\log p_{\theta }\left(a_t^n\mid s_t^n\right)\end{array}$

公式拆解

1. 第一行：$?{\bar{R}}_{\theta }={\sum }_{\tau }R(\tau )?p_{\theta }(\tau )$

   • 这里计算的是预期奖励 ${\bar{R}}_{\theta }$ 对策略参数 $\theta$ 的梯度。
   • ${\sum }_{\tau }$ 表示对所有可能的行动序列KaTeX parse error: Can't use function '\(' in math mode at position 1: \?(?\tau\)求和。
   • $R(\tau )$ 是一个特定行动序列的奖励。
   • $?p_{\theta }(\tau )$ 是该行动序列发生概率的梯度。

2. 第二行：利用概率的性质转换公式。

   • $\frac{?p_{\theta }(\tau )}{p_{\theta }(\tau )}$ 变成 $?\log p_{\theta }(\tau )$。这是因为梯度和对数的数学关系。

3. 第三行：${\mathbb{E}}_{\tau ～{\rho }_{\theta }(\tau )}[R(\tau )?\log p_{\theta }(\tau )]$

   • 这里转换成了预期值的形式，$\mathbb{E}$ 表示期望值，即按照当前策略 $\theta$ 下行动序列 $\tau$ 的分布 ${\rho }_{\theta }(\tau )$ 来计算。

4. 第四行：用采样的方法来近似计算这个期望值。

   • $\frac{1}{N}{\sum }_{n=1}^{N}R({\tau }^n)?\log p_{\theta }({\tau }^n)$ 是通过从策略 $\theta$ 中采样 (N) 个行动序列来近似这个期望值。

5. 第五行：进一步展开，考虑每个行动序列中的每个时间步。

   • ${\sum }_{t=1}^{T_n}R({\tau }^n)?\log p_{\theta }(a_t^n|s_t^n)$ 表示对每个行动序列中的每个动作 $(a_t^n)$ 和状态 $(s_t^n)$ 计算梯度的总和。

这个公式是策略梯度算法中用于计算策略梯度的一个详细公式。

它展示了如何通过梯度上升来更新策略参数 $\theta$，以便最大化总奖励 ${\bar{R}}_{\theta }$。我们可以按步骤拆解这个公式，以更容易理解的方式解释每个部分。

时间流程拆解

1. 开始：智能体在环境中执行动作，根据其策略 $(p_{\theta })$ 生成行动序列 $(\tau )$。

2. 收集数据：智能体收集一系列行动序列和相应的奖励 $(R(\tau ))$。

3. 计算梯度：对于每个采样的行动序列，计算 $(R({\tau }^n)?\log p_{\theta }({\tau }^n))$。这个步骤涉及到计算每个动作的概率的对数的梯度，并乘以相应的总奖励。

4. 平均梯度：对所有采样的行动序列计算的梯度求平均，得到对策略参数 $(\theta )$ 的平均更新方向。

5. 更新策略：最后，使用这个平均梯度来更新策略参数 $(\theta )$，以期望在未来的行动序列中获得更高的奖励。

改进策略

设置基线：适用于减小方差、加速训练效率

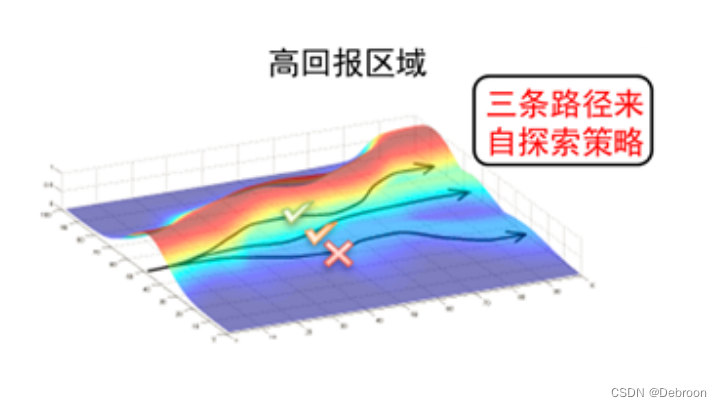
彩色的区域可能代表了不同的奖励值。

• 红色可能是高奖励区域
• 蓝色可能是低奖励区域

曲面上的箭头显示了优化过程中参数更新的路径，指向梯度的方向，即朝向奖励更高的区域。

• 不带基线的策略梯度：在没有基线的情况下，智能体可能会对每一步获得的奖励做出反应，不论这些奖励是高还是低。

  这可能导致智能体沿着曲面上的梯度盲目地寻找更高奖励的区域，这样的路径可能会很曲折，因为它会对每一个小波动都做出反应（打 X 的线）。

• 带基线的策略梯度：引入基线之后，智能体在更新其策略时，会考虑与基线的差异，而不仅仅是奖励的绝对值。

  这意味着，如果智能体在某个状态获得的奖励高于基线，它会认为这是一个好的行为，并倾向于未来重复这个行为；如果低于基线，则相反。

  这可以帮助智能体更平滑地沿着梯度上升的方向移动，避免了对奖励的小波动作出过度反应，最终可能找到一个更优化的路径。

在图中，如果我们将基线想象为一条穿过曲面的水平线，那么智能体的目标就是找到一个稳定的上升路径，而不是在每一个小坡度上都上下波动。

通过这种方式，基线就像是一个过滤器或稳定器，帮助智能体更有效地导航在奖励空间中，最终找到高奖励的顶峰。

$?{\bar{R}}_{\theta }\approx \frac{1}{N}{\sum }_{n=1}^N{\sum }_{t=1}^{T_n}\underset{\mathbf{Advantage}}{\underbrace{\left(R\left({\tau }^n\right)?b\right)}}??\log p_{\theta }\left(a_t^n\mid s_t^n\right)$

1. $?{\bar{R}}_{\theta }$：这表示我们要计算的目标，即策略的预期奖励 ${\bar{R}}_{\theta }$ 对策略参数 $\theta$ 的梯度。我们的目的是通过调整 $\theta$ 来最大化预期奖励。

2. $\frac{1}{N}{\sum }_{n=1}^N$：这表示取平均的操作。我们在许多不同的情况（称为情景或轨迹，表示为 ${\tau }^n$）下测试策略，并对结果取平均。这有助于我们得到一个更稳定、更普遍适用的策略更新。

3. ${\sum }_{t=1}^{T_n}$：这表示我们在每个轨迹中考虑每个时间步骤 (t)。对于每个时间步骤，智能体都会做出一个决策 $a_t^n$，并观察到结果 $s_t^n$。

4. $\left(R\left({\tau }^n\right)?b\right)$：这是“优势”（Advantage）函数部分，表示每个轨迹的总奖励 $R({\tau }^n)$ 减去一个基线 (b)。基线 (b) 通常是一个估计的平均奖励，这样优势就表示了在特定情况下获得的奖励比平均情况好多少。

5. $?\log p_{\theta }(a_t^n|s_t^n)$：这是策略梯度的核心部分。它表示智能体在时间步 (t)，给定状态 $s_t^n$，采取动作 $a_t^n$ 的策略的对数概率对参数 $\theta$ 的梯度。

流程顺序：

1. 生成轨迹：智能体在环境中按照当前策略 $\theta$ 行动，生成多个轨迹 ${\tau }^n$。

2. 计算每个轨迹的总奖励：对于每个轨迹，计算其获得的总奖励 $R({\tau }^n)$。

3. 计算优势：对每个轨迹，计算其优势，即总奖励减去基线 (b)。

4. 计算策略梯度：对于轨迹中的每个时间步骤，计算策略的对数概率关于参数 $\theta$ 的梯度。

5. 求和和平均：将所有轨迹的策略梯度加起来，然后除以轨迹的数量 (N)，得到平均梯度。

6. 更新策略参数：使用这个平均梯度来更新策略参数 $\theta$。

通过这个过程，策略梯度方法能够利用经验（即轨迹）来指导策略参数的更新，从而使智能体在环境中表现得更好。

归因分配 Credit Assignment：

归因分配，用于决定如何将模型输出中的误差分配到模型内部的各个参数上。

是确定每个参数对最终输出误差贡献多少的过程，这对于训练过程中的参数更新至关重要。

当一个神经网络在训练过程中生成一个输出并且与期望的输出进行比较时，它会产生一个误差信号，使得模型能够从错误中学习并调整自身。

归因分配的任务是将这个误差信号逆向传播回网络中，从而可以计算出每个参数（通常是权重）应该如何调整以减少未来的输出误差。

归因分配在强化学习中也非常重要，它帮助确定一个给定的动作和策略中的特定决策对最终奖励的贡献度。

目标函数，所有时间步的状态-动作对，都使用同样的奖励进行加权，但同一个时间步当中，一部分动作是好的，另一部分是不好的。

如果我们把每次选择都看得一样重要，那就像是说每个选择都帮助你找到宝藏一样。

但这并不公平，因为有些选择可能真的帮助了你，而有些可能就没那么重要。

所以，我们不能给所有选择都用同样的权重，贡献越多就应该分配的功劳更多。

为此，

• 每一步给小提示：这就像是游戏中的小提示告诉你，你的选择是好是坏。这样你就知道哪些选择更可能帮你找到宝藏。

• 回想一下：完成游戏后，回想一下你做的每个选择，想想哪些选择真的帮助了你。

• 记录并学习：记录你每次玩游戏时的选择，看看哪些经常出现在成功找到宝藏的游戏里。

数学表达：

• $?{\bar{R}}_{\theta }\approx \frac{1}{N}{\sum }_{n=1}^N{\sum }_{t=1}^{T_n}({\sum }_{t^{\prime }=t}^{T_n}{\gamma }^{t^{\prime }?t}{r}_{t^{\prime }}^n?b)??\log p_{\theta }\left(a_t^n\mid s_t^n\right)$

1. 每一步给小提示：

   • 在公式中，$?\log p_{\theta }(a_t^n\mid s_t^n)$ 这部分代表了给出小提示。
   • 它是告诉我们，基于当前的规则（或称策略）$p_{\theta }$，在某个特定的情况下$(s_t^n)$，选择某个行动 $(a_t^n)$ 有多好。
   • 这个提示就像是一个指示，告诉我们应该如何调整规则，使得好的选择更频繁，坏的选择更少。

2. 回想一下：

   • 公式中的 ${\sum }_{t^{\prime }=t}^{T_n}{\gamma }^{t^{\prime }?t}{r}_{t^{\prime }}^n$ 是回想过程。这里我们计算从当前步骤 ( t ) 开始到游戏结束时的所有奖励 $r_{t^{\prime }}^n$，并且还要考虑每一步的时间距离（通过 ${\gamma }^{t^{\prime }?t}$，也就是折扣因子，来减少远处的奖励对当前影响）。
   • 这样做是为了理解过去的每个选择对于获得的奖励有多少贡献。

3. 记录并学习：

   • 最外层的求和 $\frac{1}{N}{\sum }_{n=1}^N{\sum }_{t=1}^{T_n}$ 表示记录并学习。
   • 这里我们对所有玩过的游戏（或者尝试的路径）进行总结，计算每一步行动对最终结果的平均贡献。
   • 这是通过多次尝试和记录来学习哪些行动通常会导致更好的结果。

在这个公式中，( b ) 通常是一个基线值或称为偏差，它帮助我们区分哪些奖励是因为特定的动作而获得，而不是随机发生的（上文有写）。

评论家：DQN算法

请猛击：【OpenAI Q* 超越人类的自主系统】DQN ：Q-Learning + 深度神经网络