模式识别与机器学习-概率图模型
模式识别与机器学习-概率图模型
谨以此博客作为复习期间的记录
概率图模型三大基本问题
概率图模型通常涉及三个基本问题,即表示(Representation)、推断(Inference)和学习(Learning)。这三个问题是概率图模型中关键的核心概念。
-
表示(Representation):表示问题涉及选择合适的图结构来描述变量之间的依赖关系和概率分布。
-
推断(Inference):给定观测数据,逆向推理,回答非确定性问题。
-
学习(Learning):学习问题是指从数据中学习模型的参数或者图结构。在概率图模型中,学习包括参数学习和结构学习。参数学习是指从数据中估计模型中的参数,使得模型能够最好地拟合观察到的数据。结构学习是指从数据中学习最优的图结构,确定变量之间的依赖关系。
表示
推断

学习

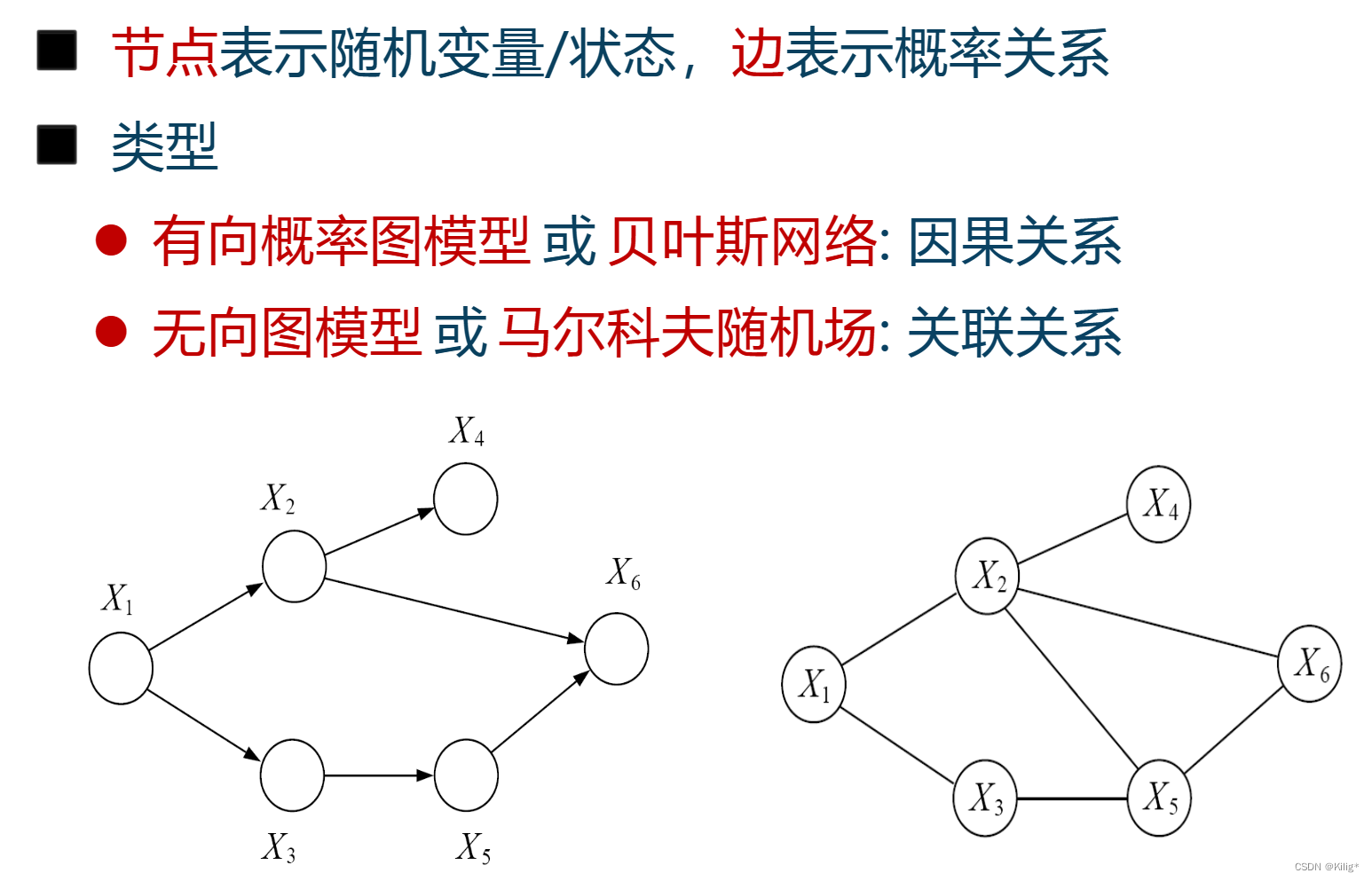
有向概率图模型
例子
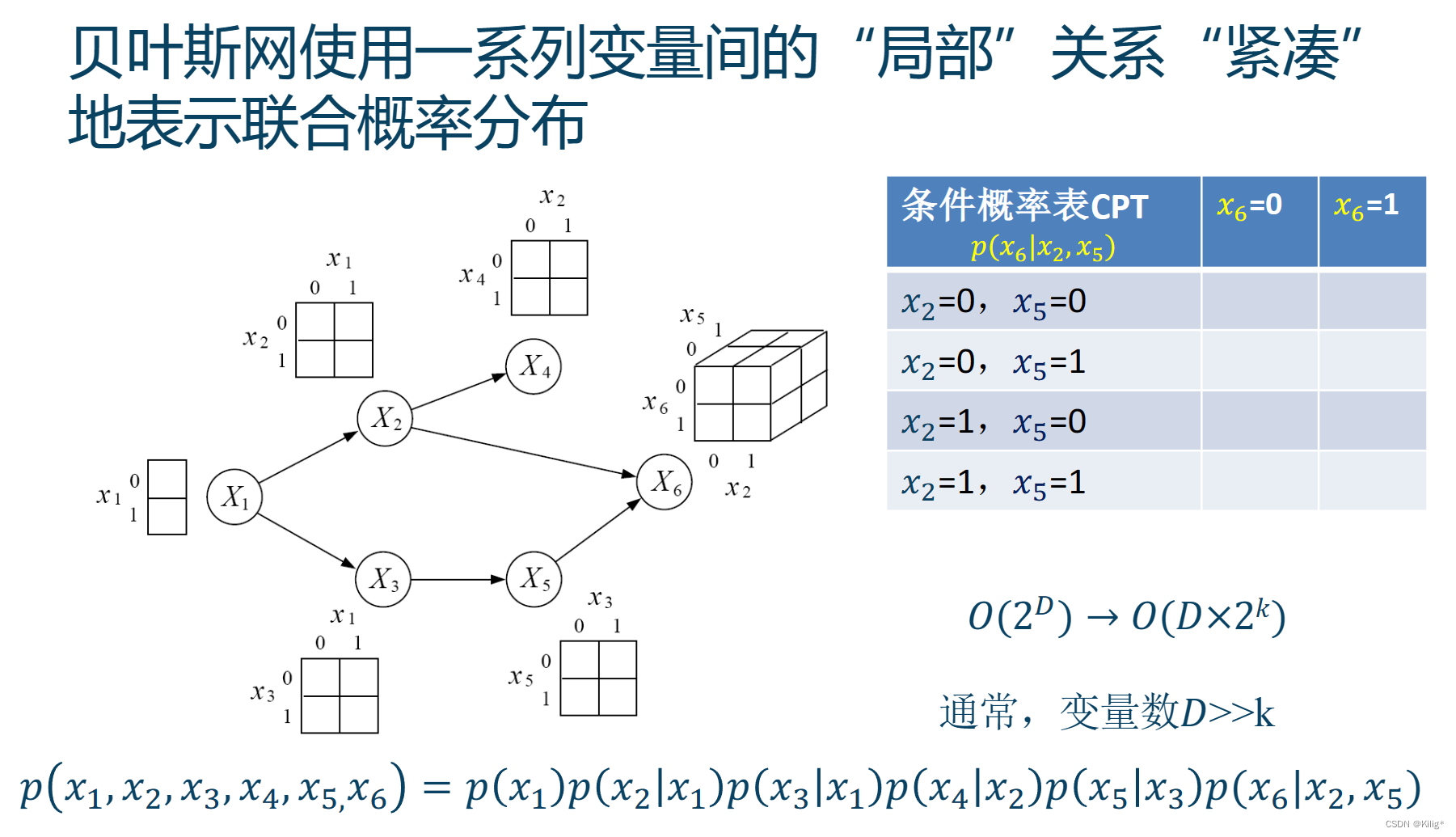
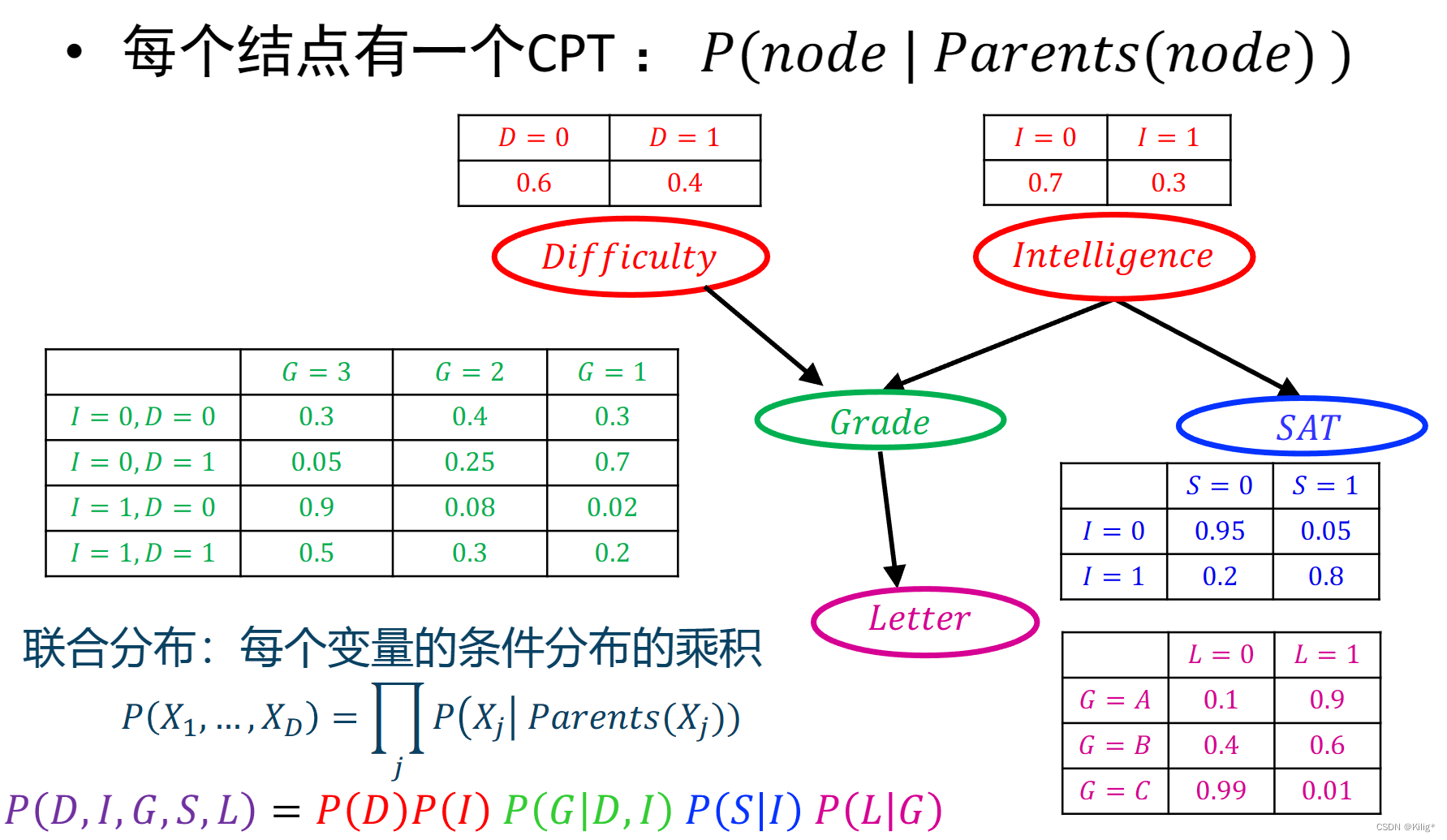
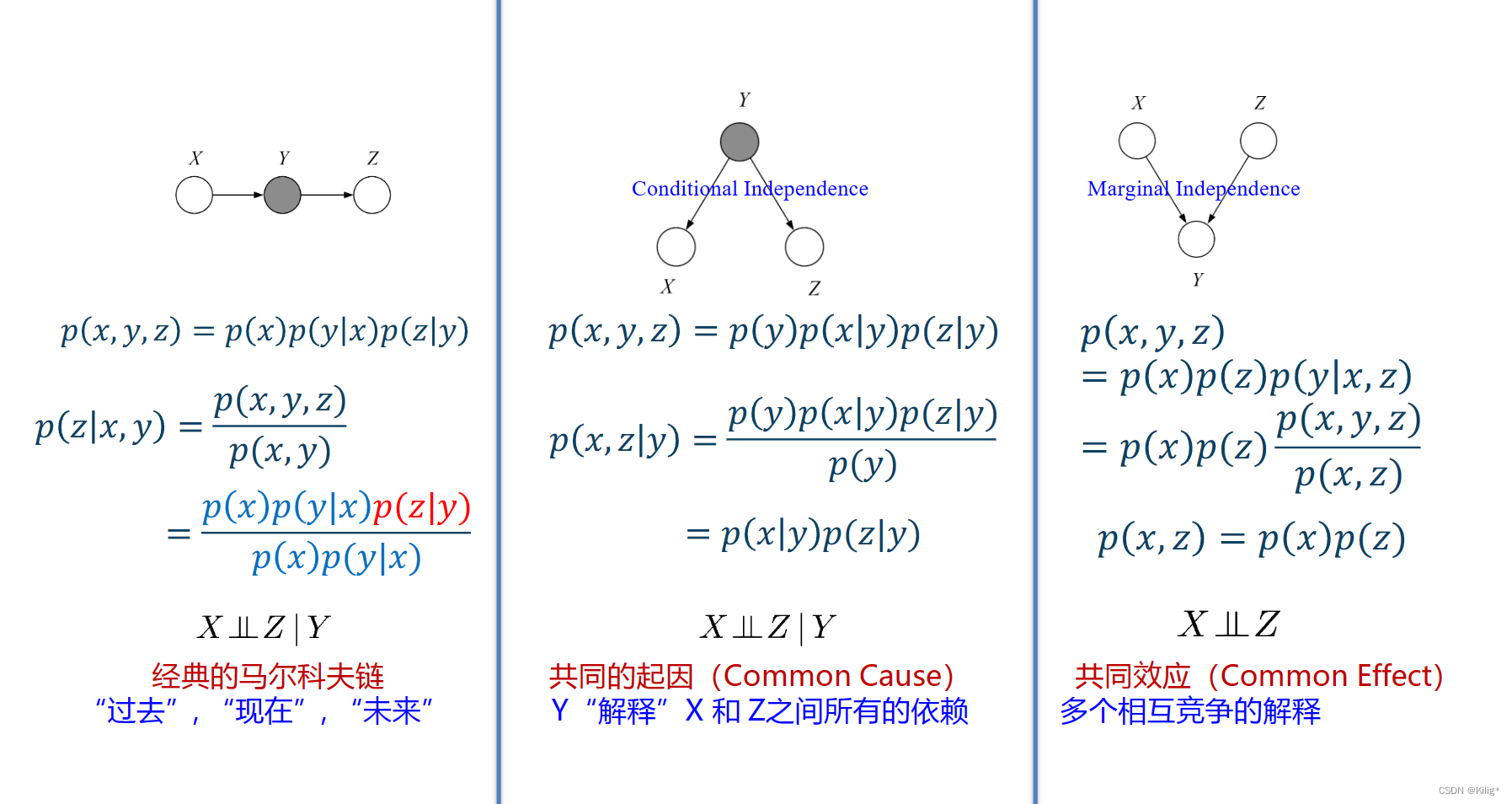
三种经典的图
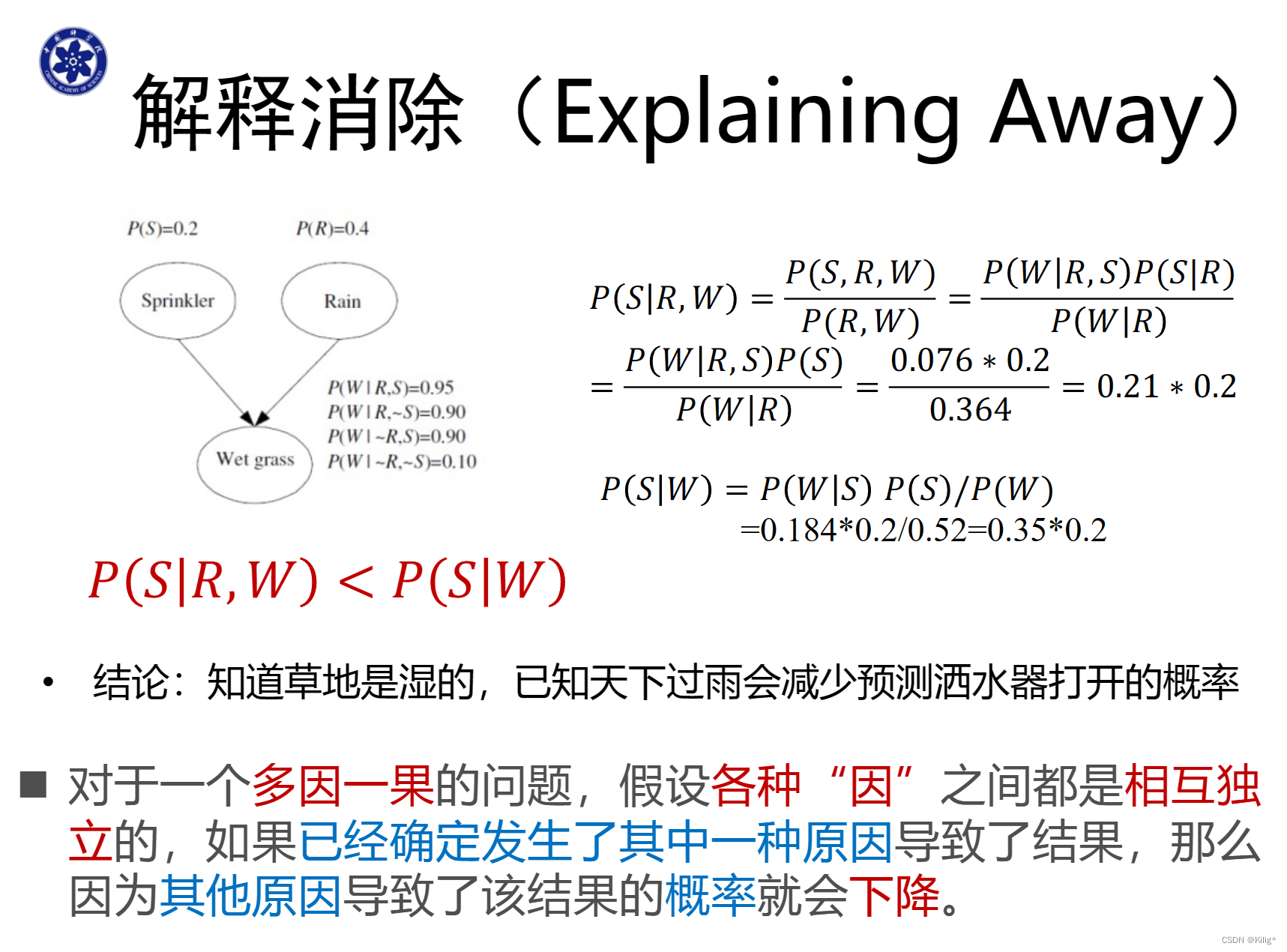

HMM
隐马尔可夫模型(Hidden Markov Model,HMM)是一种用于建模时序数据的统计模型。它是由马尔可夫链演变而来,主要用于描述具有隐藏状态(隐状态)的序列数据,并且这些隐藏状态生成了可观测的数据序列。
HMM 主要包括三个核心要素:
-
隐藏状态(Hidden States):表示模型中不可直接观测到的状态。这些状态对应着一个系统内部的“隐藏”状态,它们在时间上以马尔可夫性质进行转移,即当前状态的转移只依赖于前一个状态。在HMM中,隐藏状态是不可见的,只能通过可观测的数据间接推断。
-
观测序列(Observations):与隐藏状态相关联的可观测数据序列。这些观测值可以是文本、声音、图像或者任何连续或离散的数据。每个隐藏状态都与一个观测状态相关联,通过这些观测状态可以间接推断隐藏状态。
-
状态转移概率和观测概率:HMM包括状态转移概率和观测概率。状态转移概率表示从一个隐藏状态转移到另一个隐藏状态的概率分布;观测概率表示在特定隐藏状态下观测到某个观测状态的概率分布。

隐马尔可夫模型(HMM)通常涉及三个经典问题,这些问题是在概率图模型中对HMM进行推断和分析时所面临的核心问题:
-
评估(Evaluation):
- 问题描述:给定一个HMM模型(包括状态转移概率、观测概率)、观测序列,计算在该模型下观测序列出现的概率。
- 解决方法:使用前向算法(Forward Algorithm)或后向算法(Backward Algorithm)来计算给定模型下观测序列的概率。
-
解码(Decoding):
- 问题描述:已知一个HMM模型和观测序列,找到最可能产生该观测序列的对应隐藏状态序列。
- 解决方法:通过维特比算法(Viterbi Algorithm)找到对应于给定观测序列的最可能的隐藏状态序列。该序列通常被称为最优路径或者最可能的状态序列。
-
学习(Learning):
- 问题描述:根据观测序列,估计或学习HMM的模型参数(状态转移概率和观测概率)。
- 解决方法:使用Baum-Welch算法(也称为期望最大化算法,EM算法的一种)或者是最大似然估计(Maximum Likelihood Estimation,MLE)方法来更新和优化HMM的参数,以使得模型更好地拟合观测数据。
这三个问题通常是在HMM中进行建模、分析和应用时需要解决的关键问题。评估问题涉及计算观测序列的概率,解码问题涉及找到最可能的隐藏状态序列,而学习问题则涉及从数据中估计HMM的参数。解决这些问题使得HMM能够在多个领域中发挥重要作用,例如语音识别、自然语言处理、生物信息学等。
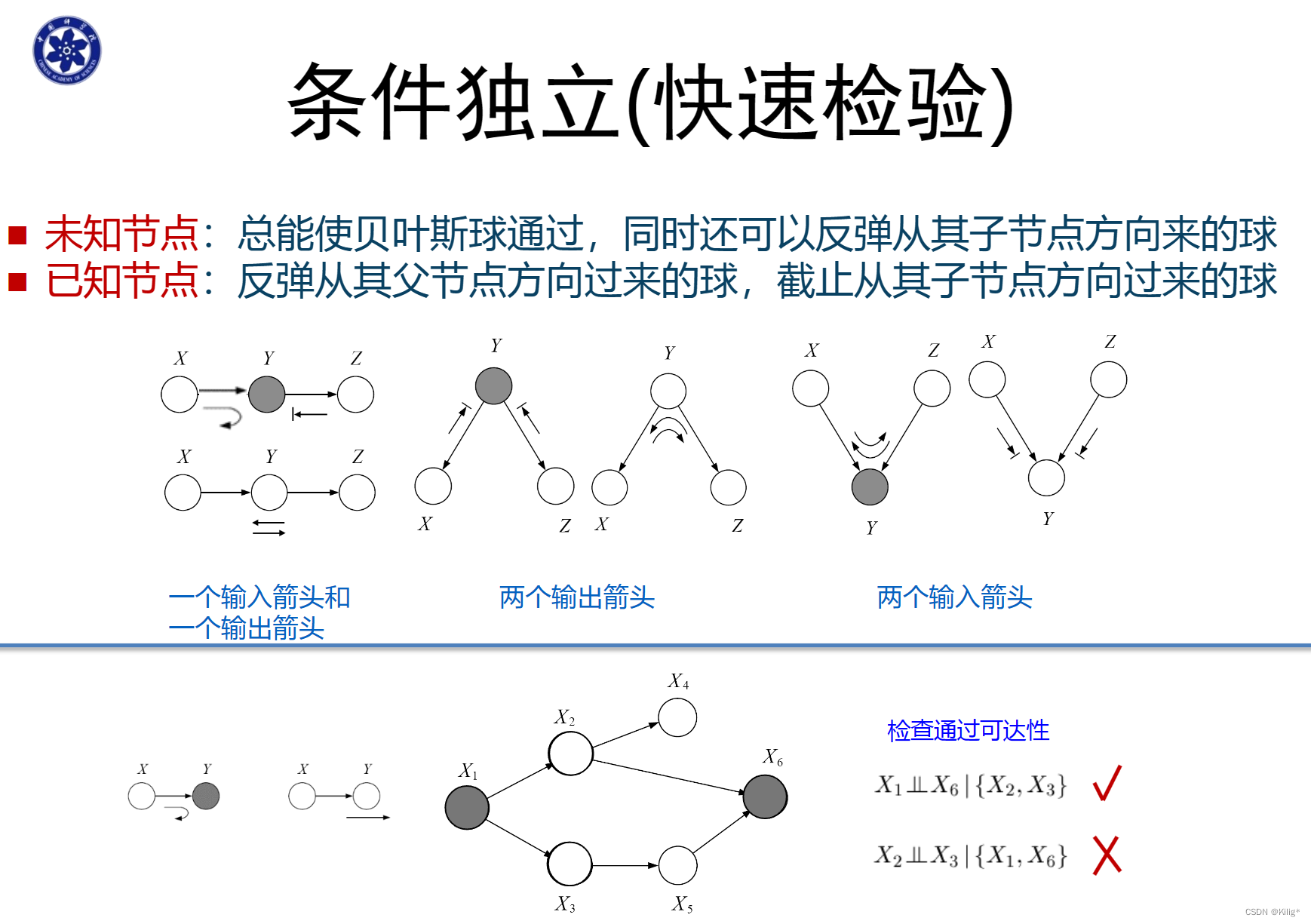
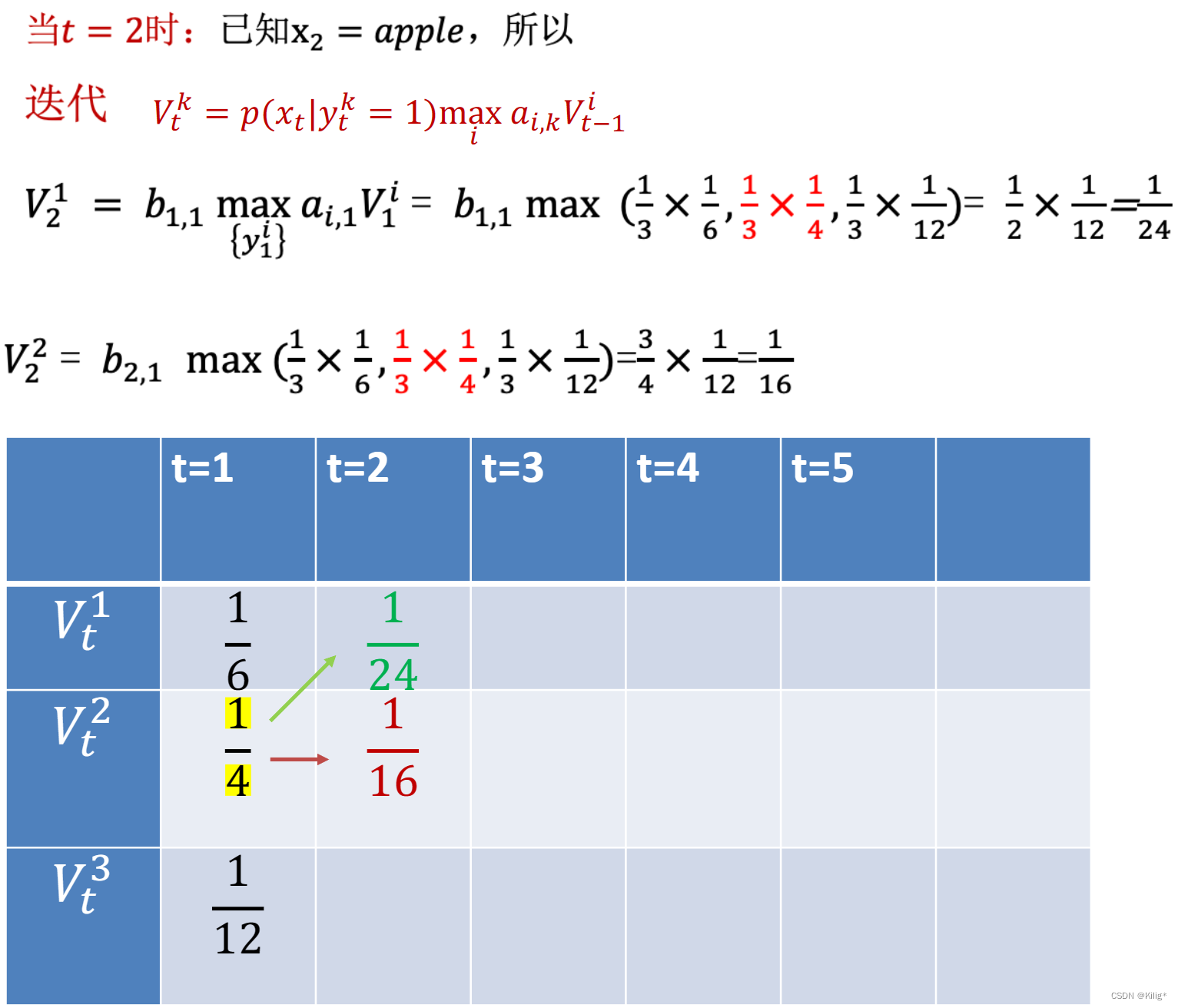
Viterbi 算法
维特比算法(Viterbi Algorithm)是用于在隐马尔可夫模型(HMM)中解码的一种动态规划算法。它能够在给定观测序列的情况下,寻找最有可能的隐藏状态序列。
假设有一个HMM模型,其中包含隐藏状态集合为 S = { S 1 , S 2 , … , S N } S = \{S_1, S_2, \dots, S_N\} S={S1?,S2?,…,SN?},观测状态集合为 O = { O 1 , O 2 , … , O T } O = \{O_1, O_2, \dots, O_T\} O={O1?,O2?,…,OT?},状态转移概率矩阵为 A A A,观测概率矩阵为 B B B,初始状态概率分布为 π \pi π。
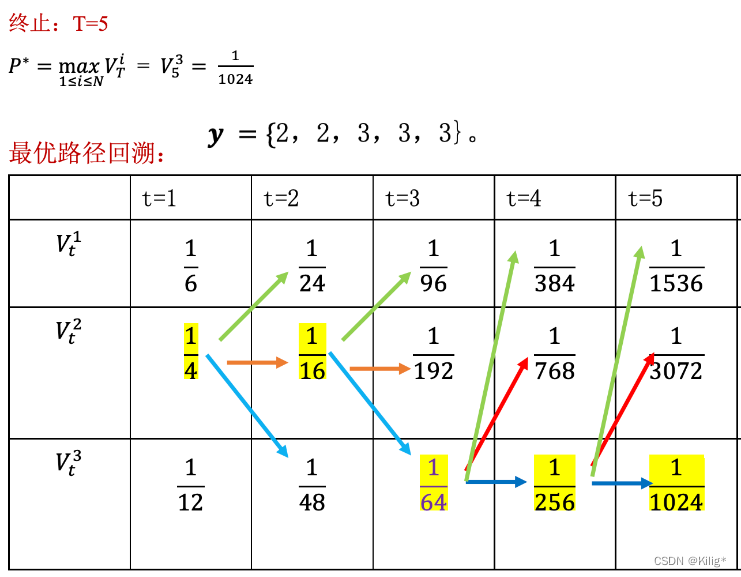
维特比算法的核心是通过递推计算每个时刻的最优路径概率以及对应的最优路径。由以下一个案列介绍维特比算法的流程。





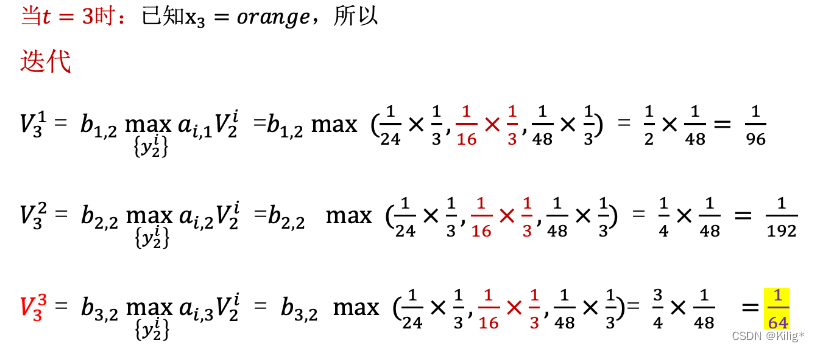
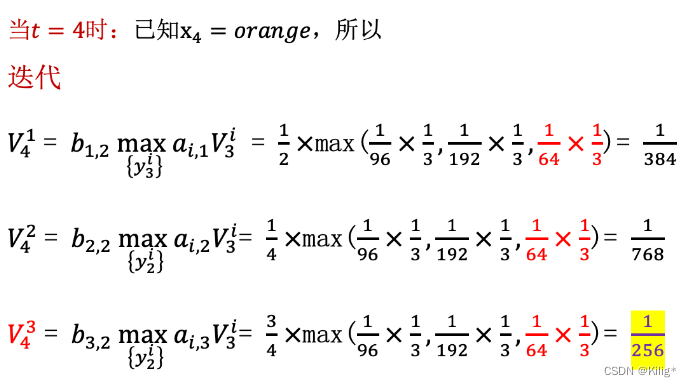

本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!