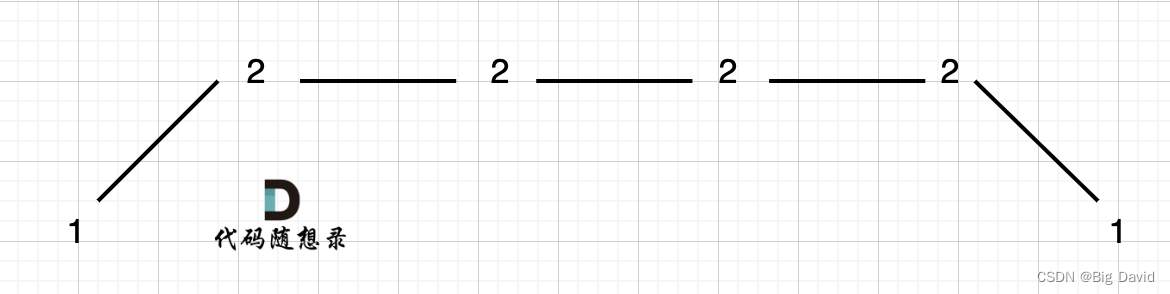代码随想录刷题题Day25
刷题的第二十五天,希望自己能够不断坚持下去,迎来蜕变。😀😀😀
刷题语言:C++
Day25 任务
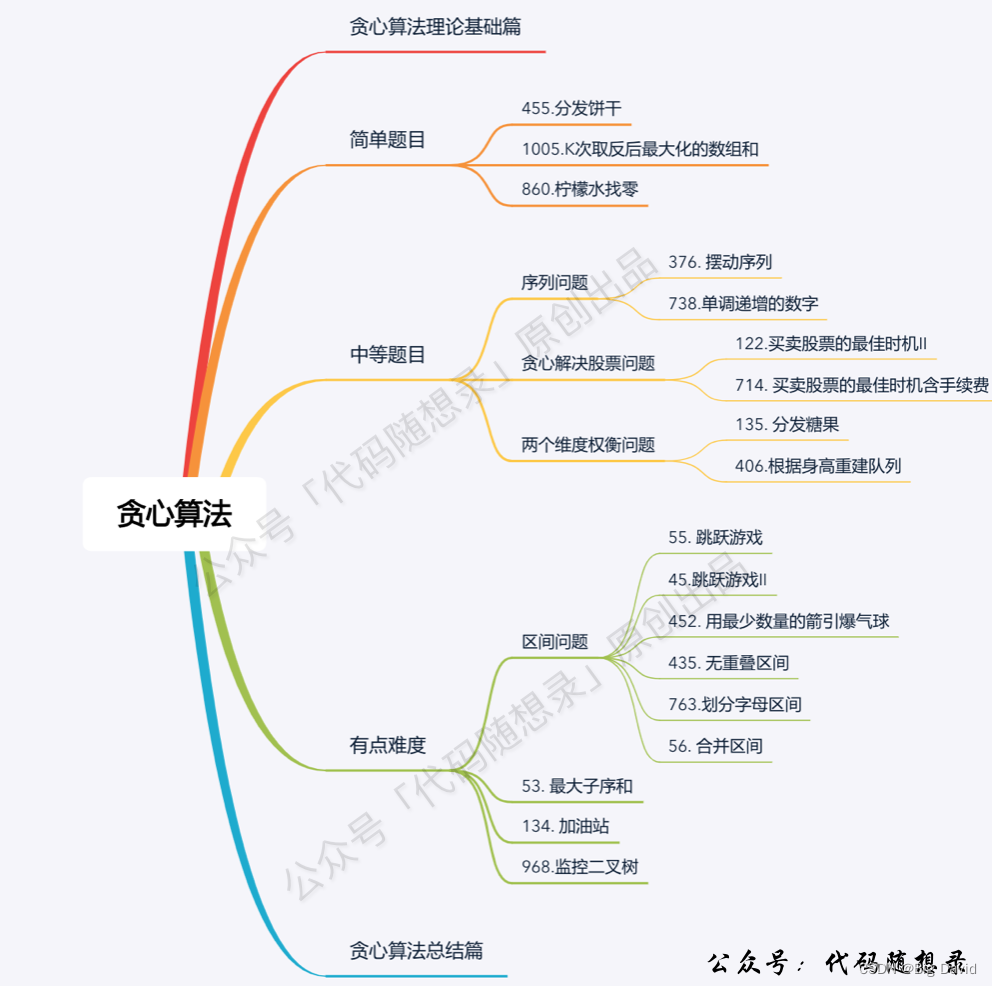
● 理论基础
● 455.分发饼干
● 376. 摆动序列
● 53. 最大子序和
1 理论基础
了解贪心算法 就了解它没有规律的本质
贪心的本质是选择每一阶段的局部最优,从而达到全局最优
贪心的套路:并没有固定的套路,唯一的难点就是如何通过局部最优,推出整体最优
贪心的一般解题步骤:
(1)将问题分解为若干个子问题
(2)找出适合的贪心策略
(3)求解每一个子问题的最优解
(4)将局部最优解堆叠成全局最优解
2 分发饼干
455.分发饼干

思路:
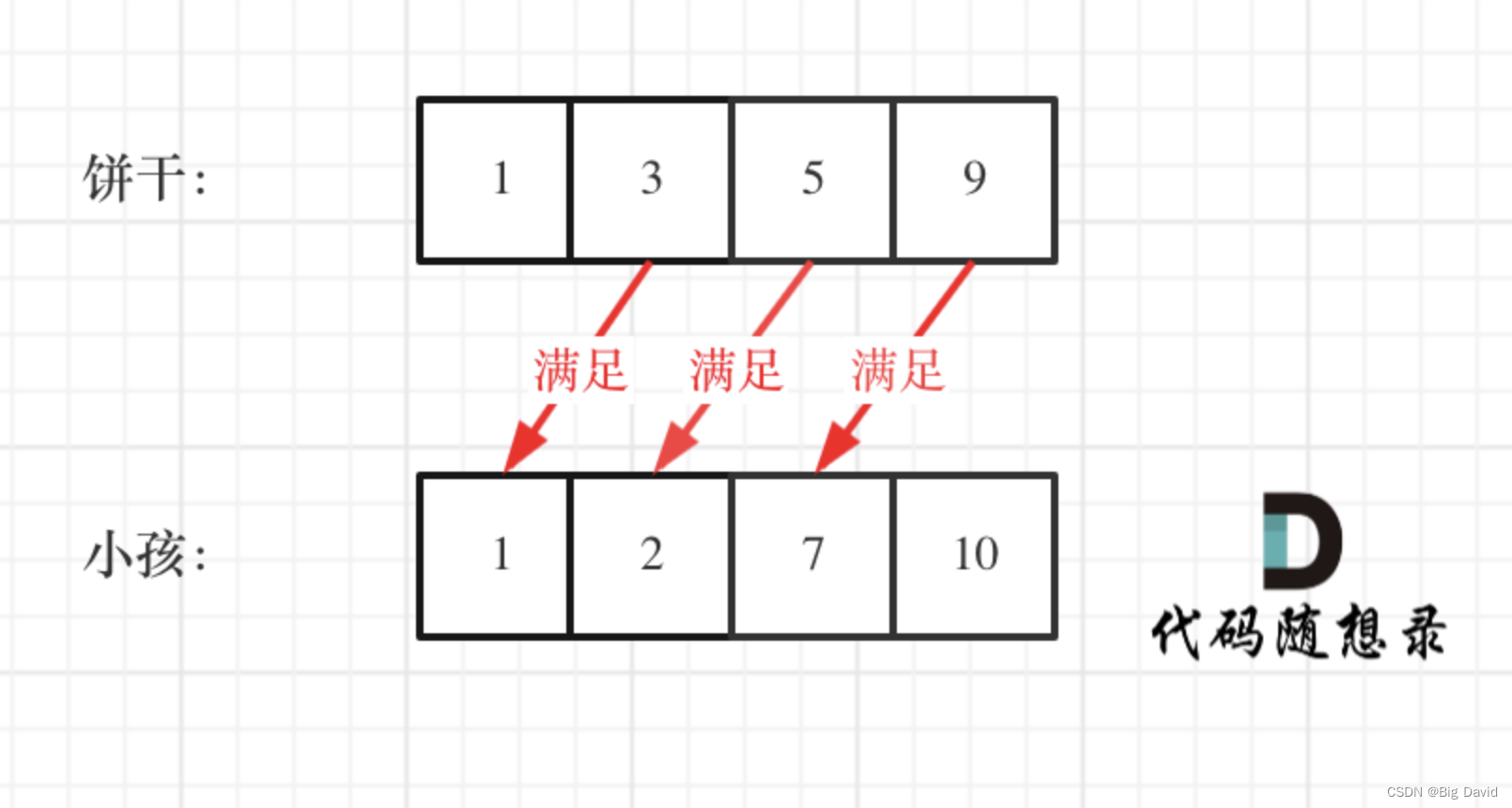
这里的局部最优就是大饼干喂给胃口大的,充分利用饼干尺寸喂饱一个,全局最优就是喂饱尽可能多的小孩
从后向前遍历小孩数组,用大饼干优先满足胃口大的,并统计满足小孩数量
C++:
class Solution {
public:
int findContentChildren(vector<int>& g, vector<int>& s) {
sort(g.begin(), g.end());
sort(s.begin(), s.end());
int result = 0;
int index = s.size() - 1;// 饼干数组的下标
for (int i = g.size() - 1; i >= 0; i--) {// 遍历胃口
if (index >= 0 && s[index] >= g[i]) {// 遍历饼干
result++;
index--;
}
}
return result;
}
};
时间复杂度:
O
(
n
l
o
g
n
)
O(nlogn)
O(nlogn)
空间复杂度:
O
(
1
)
O(1)
O(1)
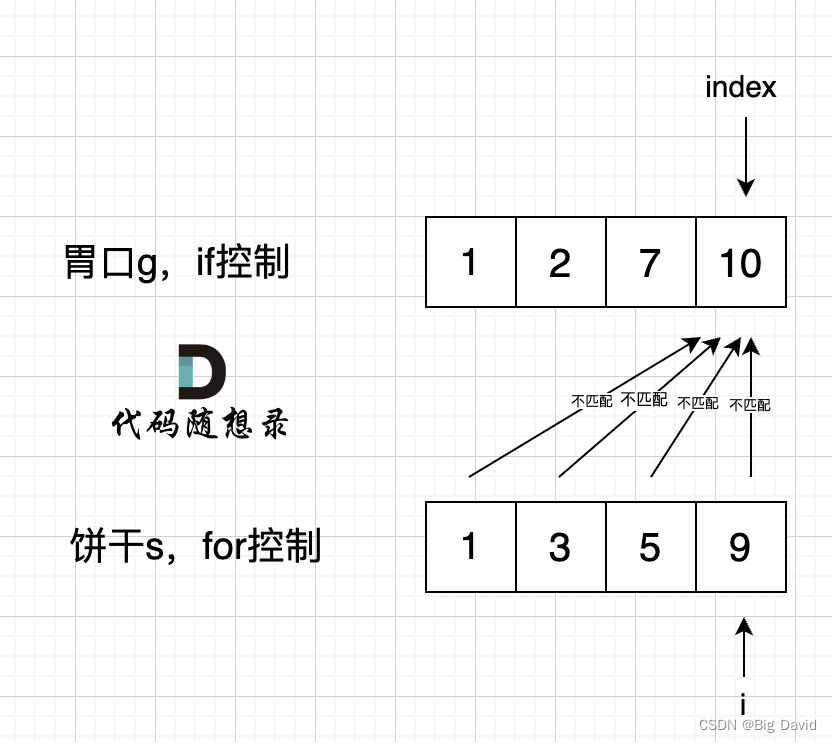
如果 for 控制的是饼干, if 控制胃口,就是出现如下情况 :
也可以换一个思路,小饼干先喂饱小胃口
C++:
class Solution {
public:
int findContentChildren(vector<int>& g, vector<int>& s) {
sort(g.begin(), g.end());
sort(s.begin(), s.end());
int index = 0;
for (int i = 0; i < s.size(); i++) {// 饼干
if (index < g.size() && g[index] <= s[i]) {
index++;
}
}
return index;
}
};
时间复杂度:
O
(
n
l
o
g
n
)
O(nlogn)
O(nlogn)
空间复杂度:
O
(
1
)
O(1)
O(1)
3 摆动序列
376. 摆动序列
思路:
通过从原始序列中删除一些(也可以不删除)元素来获得子序列,剩下的元素保持其原始顺序

局部最优:删除单调坡度上的节点(不包括单调坡度两端的节点),那么这个坡度就可以有两个局部峰值。
整体最优:整个序列有最多的局部峰值,从而达到最长摆动序列
这就是贪心所贪的地方,让峰值尽可能的保持峰值,然后删除单一坡度上的节点
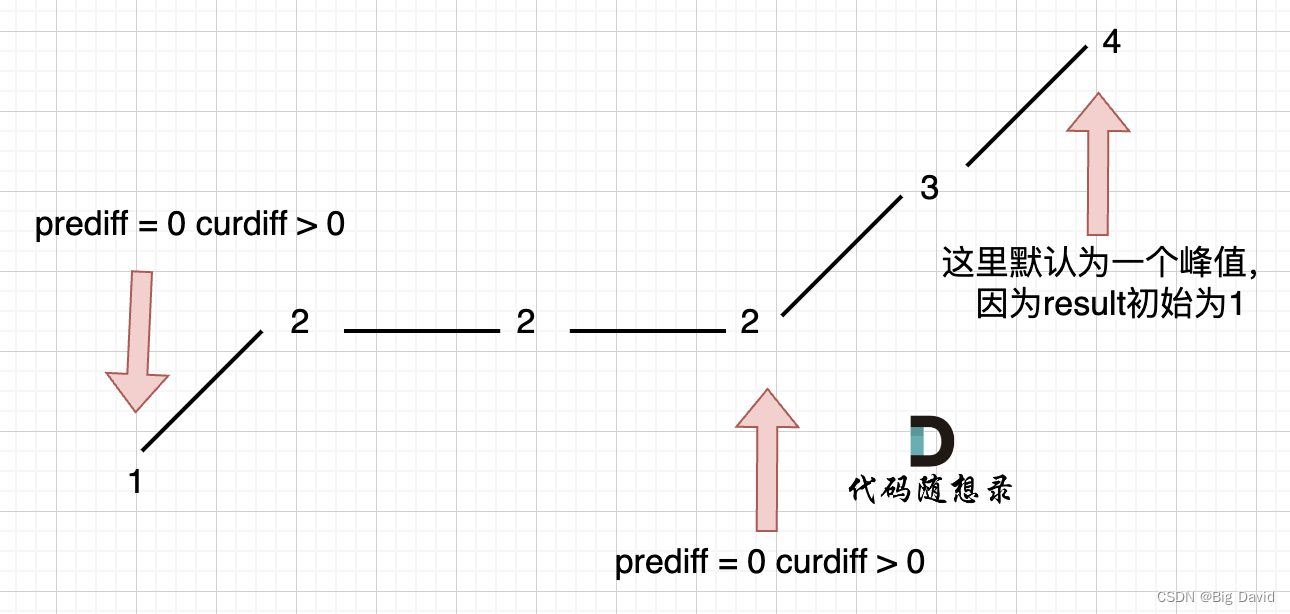
在计算是否有峰值的时候,知道遍历的下标 i ,计算 prediff(nums[i] - nums[i-1])和 curdiff(nums[i+1] - nums[i]),如果prediff < 0 && curdiff > 0 或者 prediff > 0 && curdiff < 0 此时就有波动就需要统计。
考虑三种情况:
情况一:上下坡中有平坡
统一规则,删除左边的三个2
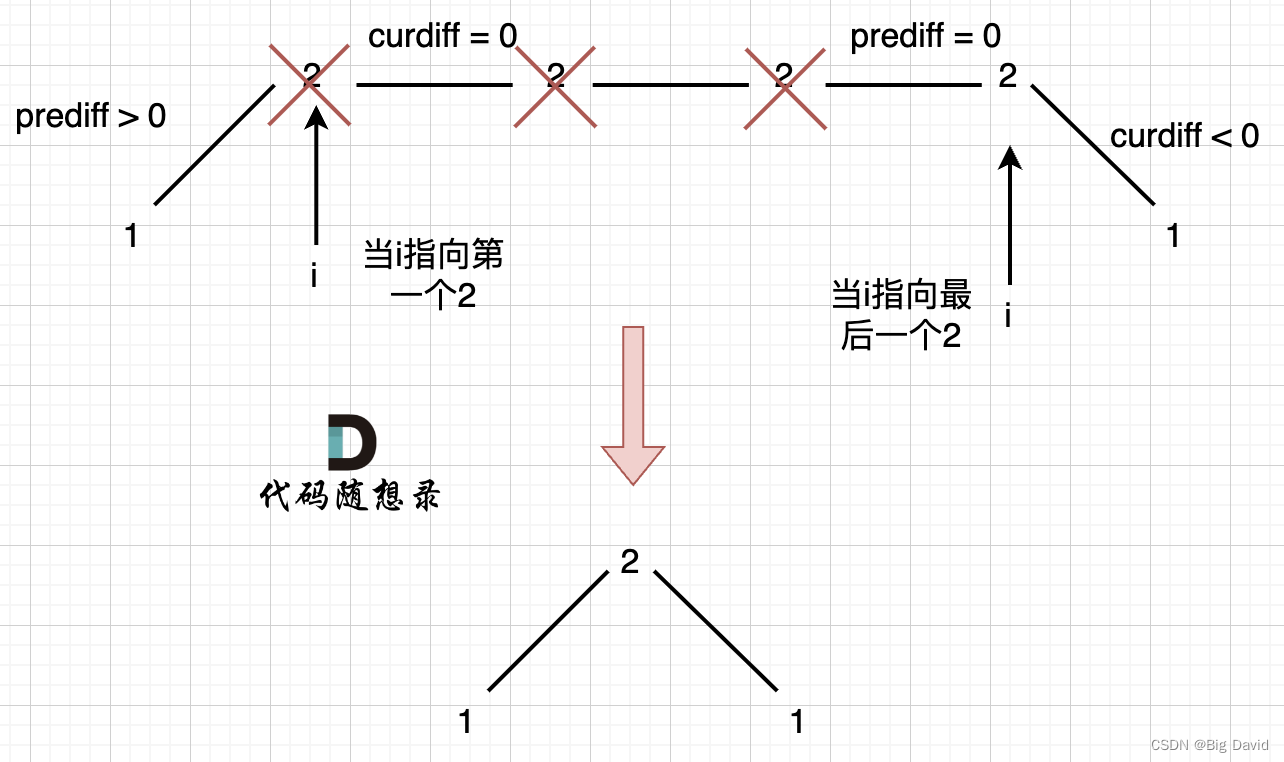
记录峰值的条件应该是:(preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)
情况二:数组首尾两端
可以假设,数组最前面还有一个数字,为了规则统一,针对序列[2,5],可以假设为[2,2,5],这样它就有坡度了即 preDiff = 0
情况三:单调坡中有平坡
只需要在 这个坡度 摆动变化的时候,更新 prediff 就行,这样 prediff 在 单调区间有平坡的时候 就不会发生变化
C++:
class Solution {
public:
int wiggleMaxLength(vector<int>& nums) {
if (nums.size() <= 1) return nums.size();
int curDiff = 0;// 当前一对差值
int preDiff = 0;// 前一对差值
int result = 1;// 记录峰值个数,序列默认序列最右边有一个峰值
for (int i = 0; i < nums.size() - 1; i++) {
curDiff = nums[i + 1] - nums[i];
// 出现峰值
if ((preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)) {
result++;
preDiff = curDiff;// 只在摆动变化的时候更新prediff
}
}
return result;
}
};
时间复杂度:
O
(
n
)
O(n)
O(n)
空间复杂度:
O
(
1
)
O(1)
O(1)
4 最大子序和
53. 最大子序和

暴力法
第一层for循环设置起始位置,第二层for寻找最大值
C++:
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int result = INT_MIN;
int count = 0;
for (int i = 0; i < nums.size(); i++) {// 设置起始位置
count = 0;
for (int j = i; j < nums.size(); j++) {// 每次从起始位置i开始遍历寻找最大值
count += nums[j];
result = count > result ? count : result;
}
}
return result;
}
};
时间复杂度:
O
(
n
2
)
O(n^2)
O(n2)
空间复杂度:
O
(
1
)
O(1)
O(1)
贪心解法
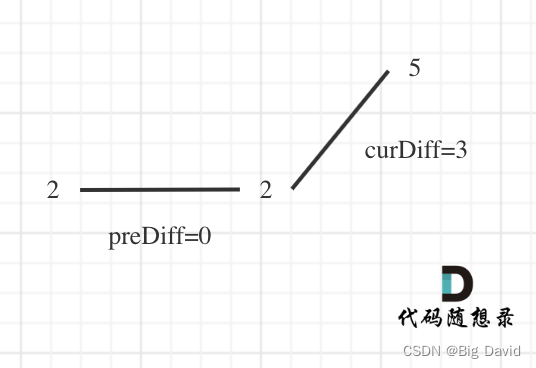
局部最优:当前“连续和”为负数的时候立刻放弃,从下一个元素重新计算“连续和”,因为负数加上下一个元素 “连续和”只会越来越小。
全局最优:选取最大“连续和”
红色的起始位置就是贪心每次取 count 为正数的时候,开始一个区间的统计

C++:
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int result = INT32_MIN;
int count = 0;
for (int i = 0; i < nums.size(); i++) {
count += nums[i];
if (count > result) result = count;// 取区间累计的最大值(相当于不断确定最大子序终止位置)
if (count < 0) count = 0;// 相当于重置最大子序起始位置,因为遇到负数一定是拉低总和
}
return result;
}
};
时间复杂度:
O
(
n
)
O(n)
O(n)
空间复杂度:
O
(
1
)
O(1)
O(1)
鼓励坚持二十六天的自己😀😀😀
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!