【基础算法】前缀和

算法介绍

什么是前缀和？？

数组: a[1], a[2], a[3], a[4], a[5], …, a[n]
前缀和 Si为数组的前 i项和
前缀和: S[i] = a[1] + a[2] + a[3] + … + a[i]

注意: 前缀和的下标建议要从 1开始, 避免进行下标的转换

s[0] = 0
s[1] = a[1]
s[2] = a[1] + a[2]

前缀和的作用

快速求出元素组中某段区间的和

一维数组求解前缀和(Si)

for循环求出 每个S[i] (将 S[0] 定义为 0, 避免下标的转换)
求 [l, r]中的和, 即为 S[r] - S[l-1]

二维数组求解前缀项和

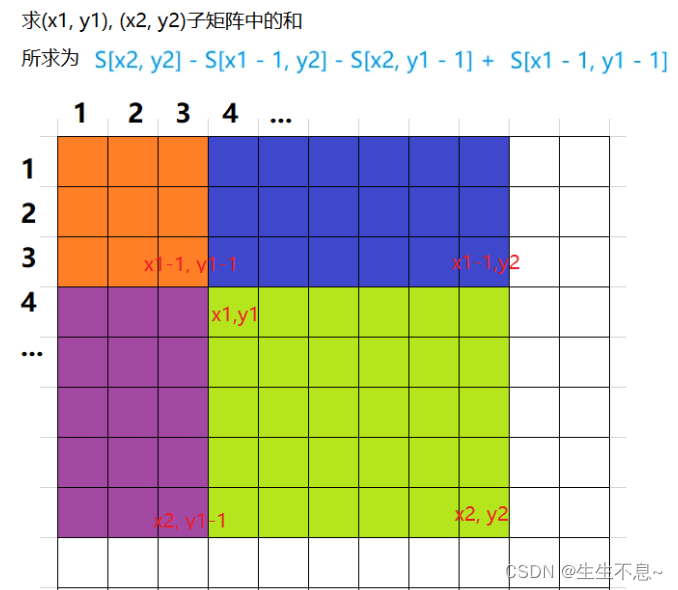
求解s[i][j]，如图所示：

示例题目1：acwing795

import java.util.*;

public class Main {
    private static int N = 100010;  // 定义数组大小, 防止越界

    public static void main(String[] args) {
        // 初始化输入值
        Scanner in = new Scanner(System.in);
        int n = in.nextInt();
        int m = in.nextInt();
        int[] arr = new int[N];
        // 注意这里是从 1开始的
        for (int i = 1; i <= n; i++)     
            arr[i] = in.nextInt();

        // s[i]代表 arr的前 i项和
        int s[] = new int[N];   
        s[0] = 0;   
        // 计算出 s[i]
        for (int i = 1; i <= n; i++)
            s[i] = s[i - 1] + arr[i];     // 注意运算方式

        // 循环输出
        while (m-- > 0) {
              int l = in.nextInt();
              int r = in.nextInt();
              System.out.println(s[r] - s[l - 1]);  // 关键
        }
    }
}

示例题目2：acwing796

代码实现如下：

import java.util.*;

public class Main {

    public static void main(String[] args) {
        // 输入值进行初始化
        Scanner in = new Scanner(System.in);
        int n = in.nextInt();
        int m = in.nextInt();
        int q = in.nextInt();
        // 初始化 arr
        int[][] arr = new int[n + 1][m + 1];
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= m; j++)
                arr[i][j] = in.nextInt();
//         输出查看 arr
//        for (int i = 1; i <= n; i++) {
//            for (int j = 1; j <= m; j++)
//                System.out.print(arr[i][j] + "  ");
//        }

        // 求解 s[i][j]
        int[][] s = new int[n + 1][m + 1];
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= m; j++)
                // 计算, 结合图来理解
                s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + arr[i][j];

        // 循环输出
        while (q-- > 0) {
            // 定位获取区间大小
            int x1 = in.nextInt();
            int y1 = in.nextInt();
            int x2 = in.nextInt();
            int y2 = in.nextInt();

            // 计算, 结合图来理解
            int res = s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1];
            System.out.println(res);
        }
    }
}

总结收获

前缀和的解题思路其实都是先得到相应的和s,然后根据公式求得对应的前缀和，公式一定要理解，不能死记硬背！一/二维前缀和模板总结如下：
一维前缀和

S[i] = a[1] + a[2] + ... a[i]
a[l] + ... + a[r] = S[r] - S[l - 1]

二维前缀和

S[i, j] = 第i行j列格子左上部分所有元素的和
以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵的和为：
S[x2, y2] - S[x1 - 1, y2] - S[x2, y1 - 1] + S[x1 - 1, y1 - 1]