计算样本距离常见的集中度量方法
2023-12-21 16:26:11
当计算两个样本之间的距离时,我们可以使用不同的距离度量方法,具体的选择通常取决于数据的性质以及任务的要求。以下是一些常见的距离度量方法:
- 欧氏距离(Euclidean Distance)
欧氏距离是最常见的距离度量方法,适用于连续型数据。对于样本向量 x 和 y,欧氏距离的计算公式为: 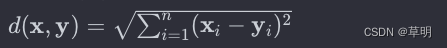
- 曼哈顿距离(Manhattan Distance)
曼哈顿距离是两点之间沿坐标轴的绝对距离之和,适用于城市街区的距离计算。对于样本向量 x 和 y,曼哈顿距离的计算公式为:

- 切比雪夫距离(Chebyshev Distance)
切比雪夫距离是两个样本向量在各个维度上差异的最大值,适用于离散型数据。对于样本向量 x 和 y,切比雪夫距离的计算公式为:
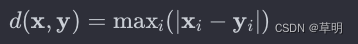
- 闵可夫斯基距离(Minkowski Distance)
闵可夫斯基距离是欧氏距离和曼哈顿距离的一般化,适用于多种数据类型。对于样本向量 x 和 y,计算公式为:

当 p=2 时,即为欧氏距离;当 p=1 时,即为曼哈顿距离。
- 余弦相似度(Cosine Similarity)
余弦相似度度量两个向量方向上的相似程度,适用于文本等高维稀疏数据。对于样本向量 x 和 y,计算公式为: 
- 汉明距离(Hamming Distance)
汉明距离度量两个等长字符串在对应位置上不同的位数,适用于处理二进制数据。对于样本向量 x 和 y,计算公式为:

- Jaccard相似度(Jaccard Similarity): Jaccard相似度度量两个集合的相似程度,适用于处理集合数据。对于样本集合 A 和 B,计算公式为:

选择合适的距离度量方法取决于你的数据类型和任务需求。在实际应用中,可能需要尝试不同的距离度量方法,并根据实验效果来选择最适合的方法。
文章来源:https://blog.csdn.net/galoiszhou/article/details/135130388
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!