八种常见顺序存储的算法
目录
1、线性枚举
1)问题描述

2)动图演示

3)示例说明
??蓝色的数据代表的是数组数据,红色的数据代表当前枚举到的数据,这样就可以遍历所有的数据进行逻辑处理了。
4)算法描述
??遍历数组,进行条件判断,条件满足则执行逻辑。这里的条件就是?枚举到的数?是否小于?当前最小值,执行逻辑为 将?当前枚举到的数?赋值给?当前最小值;
5)源码详解
int findMin(int* nums, int numsSize){
int i, min = 100000;
for(i = 0; i < numsSize; ++i) { // (1)
if(nums[i] < min) { // (2)
min = nums[i];
}
}
return min; // (3)
}- (1) 遍历数组中所有的数;
- (2)?如果?当前枚举到的数?比记录的变量
min小,则将它赋值给min;否则,不做任何处理; - (3)?最后,
min中存储的就是整个数组的最小值。
2、前缀和差分
1)问题描述

2)动图演示
3)样例分析
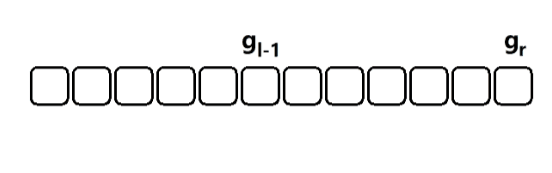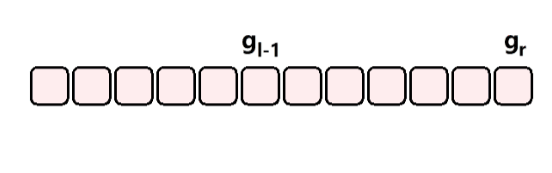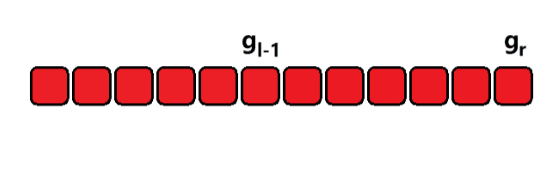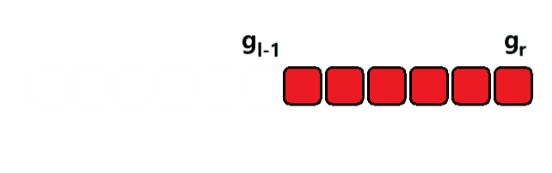
??如上图所示,只需要记录一个前缀和,然后就可以通过一次减法将区间的值计算出来。时间复杂度 O(1)。这种就是差分的思想。
原理:
sum[r] = a[1] + a[2] + a[3] + a[l-1] + a[l] + a[l + 1] ...... a[r];
sum[l - 1] = a[1] + a[2] + a[3] + a[l - 1];
sum[r] - sum[l - 1] = a[l] + a[l + 1] + ......+ a[r];
4)算法描述
??第一个枚举,利用一个数组sum,存储前?i?个元素的和。
??第二个枚举,读入?m?组数据 l,r,对每组数据,通过?O(1)?获取答案,即sum[r] - sum[l - 1]?。
5)源码详解
int sum[maxn];
int* prefixSum(int* nums, int numsSize, int m, int *l, int *r){
int i;
int *ret;
for(i = 0; i < numsSize; ++i) {
sum[i] = nums[i];
if(i)
sum[i] += sum[i-1]; // (1)
}
ret = (int *) malloc( m * sizeof(int) ); // (2)
for(i = 0; i < m; ++i) {
int leftsum = l[i] == 0 ? 0 : sum[l[i]-1]; // (3)
int rightsum = sum[r[i]];
ret[i] = rightsum - leftsum; // (4)
}
return ret;
}- (1) 计算前缀和;
- (2)?需要返回的数组;
- (3)?这里是为了防止数组下标越界;
- (4) 核心 O(1)?的差分计算;
3、双指针
1)问题描述

2)动图演示

3)样例说明
??维护两个指针?i?和?j,区间 [i,j]?内的子串,应该时刻保持其中所有字符不重复,一旦发现重复字符,就需要自增?i(即执行 i = i + 1);否则,执行 j = j + 1,直到 j?不能再增加为止。
??过程中,记录合法情况下 j ? i + 1?的最大值。
4)算法描述
??如上文所述,这种利用问题特性,通过两个指针,不断调整区间,从而求出问题最优解的算法就叫 “尺取法”,由于利用的是两个指针,所以又叫 “双指针” 算法。
??这里 “尺” 的含义,主要还是因为这类问题,最终要求解的都是连续的序列(子串),就好比一把尺子一样,故而得名。
算法描述如下:
??1)初始化 i = 0, j = i ? 1,代表一开始 “尺子” 的长度为 0;
??2)增加 “尺子” 的长度,即 j = j + 1;
??3)判断当前这把 “尺子” [i,j]?是否满足题目给出的条件:
????3.a)如果不满足,则减小 “尺子” 长度,即 i = i + 1,回到 3);
????3.b)如果满足,记录最优解,回到 2);
- 上面这段文字描述的比较官方,其实这个算法的核心,只有一句话:
满足条件时,j++;不满足条件时,i++;
- 如图所示,当区间?[i,j]?满足条件时,用蓝色表示,此时?j?自增;反之闪红,此时?i?自增。

5)源码详解
int getmaxlen(int n, char *str, int& l, int& r) {
int ans = 0, i = 0, j = -1, len; // 1)
memset(h, 0, sizeof(h)); // 2)
while (j++ < n - 1) { // 3)
++h[ str[j] ]; // 4)
while (h[ str[j] ] > 1) { // 5)
--h[ str[i] ];
++i;
}
len = j - i + 1;
if(len > ans) // 6)
ans = len, l = i, r = j;
}
return ans;
}- 1)初始化?
i = 0, j = -1,代表 s[i:j]?为一个空串,从空串开始枚举; - 2)需要维护一个哈希表,哈希表记录的是当前枚举的区间 s[i:j]?中每个字符的个数;
- 3)只推进子串的右端点;
- 4)在哈希表中记录字符的个数;
- 5)当?
h[ str[j] ] > 1满足时,代表出现了重复字符str[j],这时候左端点?i?推进,直到没有重复字符为止; - 6)记录当前最优解的长度?
j - i + 1,更新; - 这个算法执行完毕,我们就可以得到最长不重复子串的长度为 ans,并且?i?和?j?这两个指针分别只自增?n?次,两者自增相互独立,是一个相加而非相乘的关系,所以这个算法的时间复杂度为 O(n)?。
4、二分枚举
1)问题描述
2)动图演示

3)样例说明
??需要找值为?5?的这个元素。
??黄色箭头代表都是左区间端点 l,红色箭头代表右区间端点?r。蓝色的数据为数组数据,绿色的数字代表的是数组下标,初始化 l = 0,r = 7,由于数组有序,则可以直接折半,令 mid =(l+r)/2=3,则?55?一定落入区间 [0,3],这时候令 r = 3,继续执行,直到 l > r?结束迭代。
??最后,当?mid = 2?时,找到数据 5。
4)算法描述
??a)令初始情况下,数组下标从 0 开始,且数组长度为?n,则定义一个区间,它的左端点是? ? ? l =?0,右端点是 r = n?1;
??b)生成一个区间中点 mid = (l+r)/2,并且判断 mid?对应的数组元素和给定的目标值的大小关系,主要有三种:
????b.1)目标值 等于 数组元素,直接返回 mid;
????b.2)目标值 大于 数组元素,则代表目标值应该出现在区间?[mid+1,r],迭代左区间端点:l=mid+1;
????b.3)目标值 小于 数组元素,则代表目标值应该出现在区间?[l,mid?1],迭代右区间端点:r=mid?1;
??c)如果这时候 l>r,则说明没有找到目标值,返回??1;否则,回到 b)继续迭代。
5)源码详解
int search(int *nums, int numsSize, int target) {
int l = 0, r = numsSize - 1; // (1)
while(l <= r) { // (2)
int mid = (l + r) >> 1; // (3)
if(nums[mid] == target) {
return mid; // (4)
}else if(target > nums[mid]) {
l = mid + 1; // (5)
}else if(target < nums[mid]) {
r = mid - 1; // (6)
}
}
return -1; // (7)
}- (1)?初始化区间左右端点;
- (2)?一直迭代左右区间的端点,直到?左端点 大于 右端点?结束;
- (3)?
>> 1等价于除 2,也就是这里mid代表的是l和r的中点; - (4)?
nums[mid] == target表示正好找到了这个数,则直接返回下标mid; - (5)?
target > nums[mid]表示target这个数在区间?[���+1,�][mid+1,r]?中,所以才有左区间赋值如下:l = mid + 1; - (6)?
target < nums[mid]表示target这个数在区间?[�,���?1][l,mid?1]?中,所以才有右区间赋值如下:r = mid - 1; - (7)?这一步呼应了?(2),表示这不到给定的数,直接返回?
-1;
5、三分枚举
??三分枚举?类似?二分枚举?的思想,也是将区间一下子砍掉一块基本完全不可能的块,从而减小算法的时间复杂度。只不过?二分枚举?解决的是 单调性 问题。而?三分枚举?解决的是 极值问题。
6、插入排序
1)问题描述
??给定一个?n?个元素的数组,数组下标从?0?开始,采用「 插入排序 」将数组按照?「升序」排列。
2)动图演示

3)样例说明
| 图示 | 含义 |
|---|---|
| 蓝色柱形 | 代表尚未排好序的数 |
| 绿色柱形 | 代表正在执行 比较 和 移动 的数 |
| 橙色柱形 | 代表已经排好序的数 |
| 红色柱形 | 代表待执行插入的数 |
??我们看到,首先需要将?「第二个元素」?和?「第一个元素」?进行?「比较」,如果?前者?小于等于?后者,则将?后者?进行向后?「移动」,前者?则执行插入;
??然后,进行第二轮「比较」,即?「第三个元素」?和?「第二个元素」、「第一个元素」?进行?「比较」, 直到?「前三个元素」?保持有序 。
??最后,经过一定轮次的「比较」?和?「移动」之后,一定可以保证所有元素都是?「升序」?排列的。
4)算法描述
整个算法的执行过程分以下几步:
??1)?循环迭代变量 i=1→n?1;
??2)?每次迭代,令 x=a[i],j=i?1,循环执行比较 x?和 a[j],如果产生 x≤a[j]?则执 行?a[j+1]=a[j]。然后执行j=j+1,继续执行?2);否则,跳出循环,回到?1)。
5)源码详解
#include <stdio.h>
int a[1010];
void Input(int n, int *a) {
for(int i = 0; i < n; ++i) {
scanf("%d", &a[i]);
}
}
void Output(int n, int *a) {
for(int i = 0; i < n; ++i) {
if(i)
printf(" ");
printf("%d", a[i]);
}
puts("");
}
void InsertSort(int n, int *a) { // (1)
int i, j;
for(i = 1; i < n; ++i) {
int x = a[i]; // (2)
for(j = i-1; j >= 0; --j) { // (3)
if(x <= a[j]) { // (4)
a[j+1] = a[j]; // (5)
}else
break; // (6)
}
a[j+1] = x; // (7)
}
}
int main() {
int n;
while(scanf("%d", &n) != EOF) {
Input(n, a);
InsertSort(n, a);
Output(n, a);
}
return 0;
} - (1)?
void InsertSort(int n, int *a)为?插入排序?的实现,代表对a[]数组进行升序排序。 - (2) 此时
a[i]前面的?i-1个数都认为是排好序的,令x = a[i]; - (3) 逆序的枚举所有的已经排好序的数;
- (4) 如果枚举到的数
a[j]比需要插入的数x大,则当前数往后挪一个位置; - (5) 执行挪位置的?�(1)O(1)?操作;
- (6) 否则,跳出循环;
- (7) 将
x插入到合适位置;
7、选择排序
1)问题描述
??给定一个?�n?个元素的数组,数组下标从?00?开始,采用「 选择排序 」将数组按照?「升序」排列。
2)动图演示

3)样例说明
| 图示 | 含义 |
|---|---|
| 蓝色柱形 | 代表尚未排好序的数 |
| 绿色柱形 | 代表正在执行 比较 的数 |
| 橙色柱形 | 代表已经排好序的数 |
| 红色柱形 | 有两种:1、记录最小元素 2、执行交换的元素 |
??我们发现,首先从?「第一个元素」?到?「最后一个元素」?中选择出一个?「最小的元素」,和?「第一个元素」?进行?「交换」;
??然后,从?「第二个元素」?到?「最后一个元素」?中选择出一个?「最小的元素」,和?「第二个元素」?进行?「交换」。
??最后,一定可以保证所有元素都是?「升序」?排列的。
4)算法描述
整个算法的执行过程分以下几步:
??1)?循环迭代变量 i=0→n?1;
??2)?每次迭代,令 min=i,j=i+1;
??3)?循环执行比较 a[j]?和 a[min],如果产生 a[j]<a[min]?则执行 min=j。执行 j=j+1,继续执行这一步,直到 j==n;
??4)?交换 a[i]?和 a[min],回到?1)。
5)源码详解
#include <stdio.h>
int a[1010];
void Input(int n, int *a) {
for(int i = 0; i < n; ++i) {
scanf("%d", &a[i]);
}
}
void Output(int n, int *a) {
for(int i = 0; i < n; ++i) {
if(i)
printf(" ");
printf("%d", a[i]);
}
puts("");
}
void Swap(int *a, int *b) {
int tmp = *a;
*a = *b;
*b = tmp;
}
void SelectionSort(int n, int *a) { // (1)
int i, j;
for(i = 0; i < n - 1; ++i) { // (2)
int min = i; // (3)
for(j = i+1; j < n; ++j) { // (4)
if(a[j] < a[min]) {
min = j; // (5)
}
}
Swap(&a[i], &a[min]); // (6)
}
}
int main() {
int n;
while(scanf("%d", &n) != EOF) {
Input(n, a);
SelectionSort(n, a);
Output(n, a);
}
return 0;
} - (1)?
void SelectionSort(int n, int *a)为选择排序的实现,代表对a[]数组进行升序排序。 - (2)?从首元素个元素开始进行 n?1?次跌迭代。
- (3)?首先,记录
min代表当前第?i?轮迭代的最小元素的下标为?i。 - (4)?然后,迭代枚举第?i+1?个元素到 最后的元素。
- (5)?选择一个最小的元素,并且存储下标到?
min中。 - (6)?将 第?i?个元素 和 最小的元素 进行交换。
8、冒泡排序
1)问题描述
??给定一个?n?个元素的数组,数组下标从?0?开始,采用「 冒泡排序 」将数组按照?「升序」排列。
2)动图演示

3)样例说明
| 图示 | 含义 |
|---|---|
| 蓝色柱形 | 代表尚未排好序的数 |
| 绿色柱形 | 代表正在执行比较的两个数 |
| 黄色柱形 | 代表已经排好序的数 |
??我们看到,首先需要将?「第一个元素」?和?「第二个元素」?进行?「比较」,如果?前者?大于?后者,则进行?「交换」,然后再比较?「第二个元素」?和?「第三个元素」?,以此类推,直到?「最大的那个元素」?被移动到?「最后的位置」?。
??然后,进行第二轮「比较」,直到?「次大的那个元素」?被移动到?「倒数第二的位置」?。
??最后,经过一定轮次的「比较」?和?「交换」之后,一定可以保证所有元素都是?「升序」?排列的。
4)算法描述
整个算法的执行过程分以下几步:
??1)?循环迭代变量 i=0→n?1;
??2)?每次迭代,令 j=i,循环执行比较?a[j]?和 a[j+1],如果产生 a[j]>a[j+1]?则交换两者的值。然后执行 j=j+1,这时候对?j?进行判断,如果 j≥n?1,则回到?1),否则继续执行?2)。
5)源码详解
#include <stdio.h>
int a[1010];
void Input(int n, int *a) {
for(int i = 0; i < n; ++i) {
scanf("%d", &a[i]);
}
}
void Output(int n, int *a) {
for(int i = 0; i < n; ++i) {
if(i)
printf(" ");
printf("%d", a[i]);
}
puts("");
}
void Swap(int *a, int *b) {
int tmp = *a;
*a = *b;
*b = tmp;
}
void BubbleSort(int n, int *a) { // (1)
bool swapped;
int last = n;
do {
swapped = false; // (2)
for(int i = 0; i < last - 1; ++i) { // (3)
if(a[i] > a[i+1]) { // (4)
Swap(&a[i], &a[i+1]); // (5)
swapped = true; // (6)
}
}
--last;
}while (swapped);
}
int main() {
int n;
while(scanf("%d", &n) != EOF) {
Input(n, a);
BubbleSort(n, a);
Output(n, a);
}
return 0;
} - (1)?
void BubbleSort(int n, int *a)为冒泡排序的实现,代表对a[]数组进行升序排序。 - (2)?
swapped标记本轮迭代下来,是否有元素产生了交换。 - (3)?每次冒泡的结果,会执行
last的自减,所以待排序的元素会越来越少。 - (4)?如果发现两个相邻元素产生逆序,则将它们进行交换。保证右边的元素一定不比左边的小。
- (5)?
swap实现了元素的交换,这里需要用&转换成地址作为传参。 - (6)?标记更新。一旦标记更新,则代表进行了交换,所以下次迭代必须继续。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!