动态规划——斐波那契数列模型:1137.第N个泰波那契数
2023-12-16 05:11:11
文章目录
题目描述
题目链接:1137.第N个泰波那契数

算法原理
如果我们采用动态规划的思想来解决这道问题的话,我们的过程一般是分五步来解决的:
1.状态表示(最重要的)
什么是状态表示?
首先我们要先确定一个状态表示。那第一次接触动态规划的同学可能就有些疑问了,什么是状态表示呢?通俗的来讲就是,我们会先定义一个dp表,这个dp表可能是一维数组或者二维数组,简单举例一下:
我们做动态规划的流程就是搞一个dp表,然后把他填满,其中一个值可能就是我们的答案,状态表示指的就是dp表中的某个值它所代表的含义(感性理解)。如果我们去直接去百度动态规划的状态表示是什么的话,会出现一堆概念性的专有名词,要是没一两周根本搞不懂,而且会很痛苦,很容易放弃,所以刚开始学的时候我们有一个感性的认知就可以了。

状态表示怎么来的呢?
(PS:很多教学视频上来就给一个状态表示,而不说明状态表示怎么来的,那后续的步骤则显得毫无意义)
- 题目要求
- 经验(一两百道题)+题目要求
- 分析问题的过程中,发现重复子问题(表示动态规划的方式)
第三个看起来也有点抽象,但问题不大,前期跟紧我的节奏,先理解前两步,慢慢的等我们动态规划学的熟练了就会进而引出第三种了。当然也会有其它的,但我这个系列只会涉及这三个。
本题的状态表示
dp[i]:表示第i个泰波那契数的值
2.状态转移方程(最难的)
dp[i]等于什么,状态转移方程就是什么。所以我们要想尽一切办法来让之前的状态或者之后的状态来表示dp[i]。
本题的状态转移方程
题目非常贴心,已经给出:dp[i]=dp[i-1]+dp[i-2]+dp[i-3]
3.初始化(后三步完成剩下百分之一的细节问题)
根据状态转移方程来填表,保证填表的时候不越界

本题的初始化
dp[0]=0,dp[1]=1,dp[2]=1
4.填表顺序
为了填写状态的时候,所需要的状态已经计算过了。
本题的填表顺序
从左向右
5.返回值
题目要求+状态表示
本题返回值
dp[n]
代码实现
class Solution {
public:
int tribonacci(int n) {
//时间复杂度和空间复杂度都为O(N)
//处理一些越界情况
if(n <= 1)return n;
else if(n == 2)return 1;
//1.状态表示
vector<int> dp(n + 1);
//2.初始化
dp[0] = 0,dp[1] = 1,dp[2] = 1;
//3.填表顺序
for(int i = 3;i <= n;i++)
{
dp[i] = dp[i - 3] + dp[i - 2] + dp[i - 1];
}
//返回值
return dp[n];
}
};
空间优化
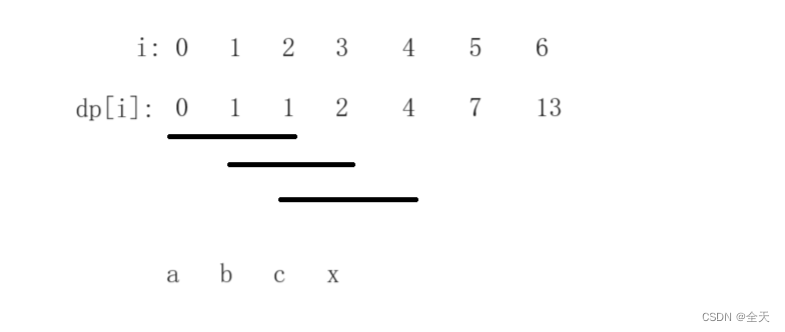
每次滚动则之前的数可以舍去。
class Solution {
public:
int tribonacci(int n) {
//滚动数组空间优化——空间复杂度从O(N)变为O(1)
//处理一些边界情况
if(n <= 1)return n;
else if(n == 2)return 1;
//初始化
int a = 0,b = 1,c = 1,x = 0;
//填表顺序
for(int i = 3;i <= n;i++)
{
x = a + b + c;
a = b;
b = c;
c = x;
}
//返回值
return x;
}
};
文章来源:https://blog.csdn.net/quantian_/article/details/135025938
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!