Python房价分析(二)随机森林分类模型
目录

往期精彩内容:
房价分析(0)反爬虫机制_python爬取房价数据-CSDN博客
Python房价分析(三)支持向量机SVM分类模型-CSDN博客
1 数据预处理
1.1 房价数据介绍
房价数据来源于上期Python爬虫所获取的数据
本文采用宜昌市二手房数据进行讲解,数据如图所示,共3000条样本,有区域、街道、房型、朝向、面积、楼层数、装修类型、房屋结构、收藏数、价格 10个特征。
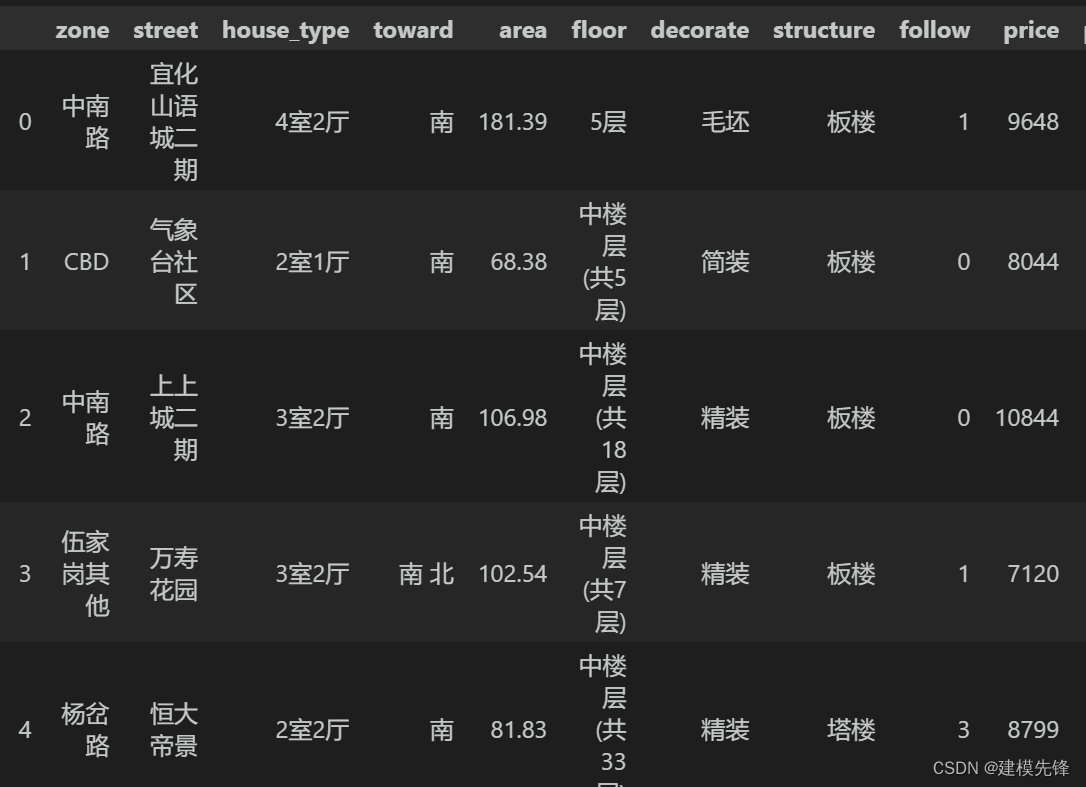
1.2 数据预处理
数据的偏离程度以及数据之间的关联性会拉大整体数据标准差、造成统计偏见以及使数据带有指向性偏好,这都会影响到我们最终模型和分析的结果,造成偏差,可见在进行统计与计算前对数据处理的必要性与重要性。
1.2.1?缺失值处理
????????对于给定的二手房数据中,可能某些特征存在一定的缺失值,当个别样本缺失某些指标数据,模型的训练就难以进行,若不对其进行缺失值填补则做分析时会被剔除进而不能参与最终的各项排名和综合评价,影响后续的数据分析。
????????因此,基于本数据相关特征指标的缺失数量占总数据的比重较小,为了不丢弃大量隐藏在删除对象中的信息,避免数据发生偏离,我们对数值型指标的缺失值进行0值填充,对于分类特征的缺失值,将“nan”(缺失值)视为有效的特征值,并为其创建指示符特征。
其中可选的插补策略包括
-
平均值mean
-
中位数median
-
众数most_frequency
-
固定值constant
1.2.2异常值处理
对于异常值,不是删除“异常数据”,而是将这些数据“拉回”到正常的值,本文通过确定指标的上下限,然后对于超过或者低于限值的数据均为限值,其上下限数值通过MAD(mean absolute deviation)即绝对值差中位数法判断,来处理因子数据集中的异常值。
#对大于97.5%分位数的因子值,或小于2.5%分位数的因子值进行调整 容易理解,去除两头,只需调节参数,量化中较常用
def extreme_percentile(series,min=0.025,max=0.975):
p = series.quantile([min,max]) # 得到上下限的值
return series.clip(p.iloc[0],p.iloc[1]) # 超出上下限的值,赋值为上下限1.2.3 数据归一化
由于数据集中大多数特征指标不满足正态分布,不能采用常规的z-score 标准化。而数据集经过异常值处理后,减小了数据归一化受离群点影响,我们采用Min-Max归一化即极差法,将数据集中列数值缩放到0和1之间,来处理量纲的问题。
讲解一下为什么需要归一化
-
归一化后加快了梯度下降求最优解的速度:如果机器学习模型使用梯度下降法求最优解时,归一化往往非常有必要,否则很难收敛甚至不能收敛;
-
归一化有可能提高精度:一些分类器需要计算样本之间的距离(如欧氏距离),例如KNN。如果一个特征值域范围非常大,那么距离计算就主要取决于这个特征,从而与实际情况相悖(比如这时实际情况是值域范围小的特征更重要)
哪些机器学习算法不需要(需要)做归一化?
-
概率模型(树形模型)不需要归一化,因为它们不关心变量的值,而是关心变量的分布和变量之间的条件概率,如决策树、RF;
-
像Adaboost、SVM、LR、Knn、KMeans之类的最优化问题就需要归一化。
1.2.4 分类特征编码
对于数据集中的多分类特征变量,把不能量化的多分类变量量化,使得每个哑变量对模型的影响都细化,从而提高模型精准率。分类变量编码能够加速参数的更新速度;使得一个很大权值管理一个特征,拆分成了许多小的权值管理这个特征多个表示,降低了特征值扰动对模型的影响,模型具有更好的鲁棒性。因此,我们采用OneHot独热编码来为其创建分类类别特征。
from sklearn.preprocessing import OneHotEncoder
# 构造数据
X_train = [['male', 'from US', 'uses Safari'],
['female', 'from Europe', 'uses Firefox'],
['female', 'from China', 'uses Safari']]
# 编码器
encoder = OneHotEncoder()
encoder = encoder.fit(X_train)
# 编码
X = [['female', 'from Europe', 'uses Safari']]
X_transform = encoder.transform(X)
X_transform.toarray() # 默认返回的是稀疏矩阵, 用toarray()方法可以转为np.array格式
>> array([[1., 0., 0., 1., 0., 0., 1.]])2 随机森林模型
2.1?模型概述
随机森林是一种集成算法(Ensemble Learning),它是属于Bagging类型。由于采用了集成算法,机器训练后得到的结果会比那些只通过单个算法得到的结果更加准确,它可以用来解决分类和回归问题[1]。随机森林需要进行模拟和迭代,它通过随机抽取样本和特征,建立多棵相互不关联的决策树,每棵决策树都能通过抽取的样本和特征得出一个预测结果,通过综合所有树的结果取平均值,得到整个森林的回归预测结果。具体算法结构如图所示。

随机森林有众多优点,如:对特征很多的数据也可以适用 , 不用降维,不需要做特征选择;可以输出特征的重要性排序,方便逻辑解释;可以判断出不同特征之间的相互影响;训练速度比较快;不容易过拟合;可以适用不平衡的数据等[2]。另外, 随机森林不仅能处理离散型数据,还能处理连续型数据,而且不需要将数据集规范化。基于以上优点,选取随机森林模型来对二手房价格进行分类与预测。
2.2 建模步骤
Step1.特征变量和目标变量提取,我们分析利用二手房价高、中、低三分类作为目标变量,把区域、街道、楼房名称、户型、朝向、建筑面积、楼层、装修、结构、关注作为特征变量;
Step2.先对特征数据集进行标准化处理,然后进行训练集和测试集数据划分,本文将原始数据集进行分割,将训练集与测试集进行划分,将前70%的数据作为训练集,后30%的数据作为测试集;
导入相关包
import pandas as pd
import numpy as np
from sklearn.ensemble import RandomForestClassifier # 随机森林分类
from sklearn.model_selection import train_test_split,GridSearchCV,cross_val_score
from sklearn.metrics import accuracy_score # 引入准确度评分函数
from sklearn.metrics import mean_squared_error
from sklearn.metrics import confusion_matrix, accuracy_score,classification_report
from sklearn import preprocessing
import warnings
warnings.filterwarnings('ignore')
import matplotlib.pyplot as plt
import matplotlib
matplotlib.rc("font", family='Microsoft YaHei')读取 预处理后的 数据
# 读取 预处理后的 数据
price_classify_data = pd.read_csv('yichang_deal.csv')
X = price_classify_data[['zone_label','street_label','type_label','toward_label','area','floor_label',
'decorate_label','structure_label','follow']]
Y = price_classify_data['price_label']
# 标准化
X = preprocessing.scale(X)
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.3, random_state=200) # 随机数种子Step3.利用Python的开源机器学习库scikit-learn构建分类模型,采用随机森林回归方法进行建模,并通过设置不同决策树数量来评估随机森林方法的分类能力。
2.3 参数搜索过程
首先我们对最重要的超参数n_estimators即决策树数量进行调试,通过不同数目的树情况下,在训练集和测试集上的均方根误差来判断


以及最优参数和最高得分进行分析,如下所示。
###调n_estimators参数
ScoreAll = []
for i in range(90,200,10):
DT = RandomForestClassifier(n_estimators = i,random_state = 1) #,criterion = 'entropy'
score = cross_val_score(DT,X_train,Y_train,cv=6).mean()
ScoreAll.append([i,score])
ScoreAll = np.array(ScoreAll)
max_score = np.where(ScoreAll==np.max(ScoreAll[:,1]))[0][0] ##这句话看似很长的,其实就是找出最高得分对应的索引
print("最优参数以及最高得分:",ScoreAll[max_score])
plt.figure(figsize=[20,5])
plt.plot(ScoreAll[:,0],ScoreAll[:,1],'r-o',label='最高得分',color='orange')
plt.xlabel('n_estimators参数')
plt.ylabel('分数')
plt.grid()
plt.legend()
plt.show()
很明显,决策树个数设置在130的时候回归森林预测模型的测试集均方根误差最小,得分最高,效果最显著。因此,我们通过网格搜索进行小范围搜索,构建随机森林预测模型时选取的决策树个数为130。
在确定决策树数量大概范围后,搜索决策树的最大深度的最高得分,如下所示。
# 探索max_depth的最佳参数
ScoreAll = []
for i in range(10,30,3):
DT = RandomForestClassifier(n_estimators = 130,random_state = 1,max_depth =i ) #,criterion = 'entropy'
score = cross_val_score(DT,X_train,Y_train,cv=10).mean()
ScoreAll.append([i,score])
ScoreAll = np.array(ScoreAll)
max_score = np.where(ScoreAll==np.max(ScoreAll[:,1]))[0][0]
print("最优参数以及最高得分:",ScoreAll[max_score])
plt.figure(figsize=[20,5])
plt.plot(ScoreAll[:,0],ScoreAll[:,1])
plt.xlabel('max_depth最佳参数')
plt.ylabel('分数')
plt.grid()
plt.legend()
plt.show() 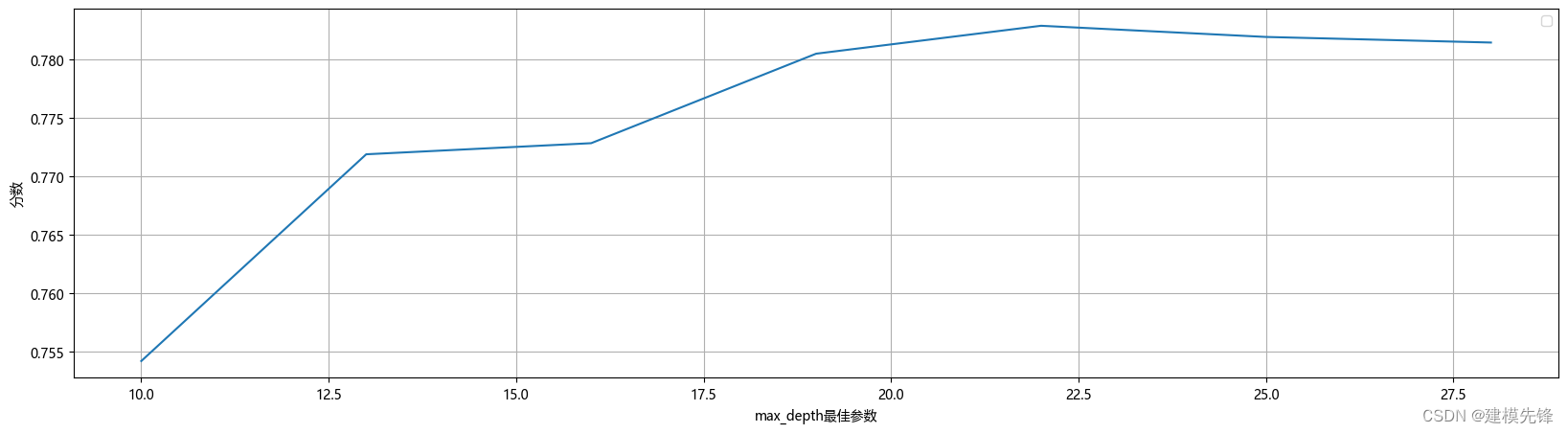
决策树的深度为22。
网格搜索调参:

通过网格搜索,我们对最终的模型超参数进行分析,得出重要超参数如表所示。采用10折交叉验证,节点分裂评价准则为基尼系数,决策树数量为128,内部节点分裂的最小样本数为2,叶子节点的最小样本数为1,树的最大深度为22,叶子节点的最大数量为50。有放回采样为True,袋外数据测试为False,划分时考虑的最大特征比例为默认值。
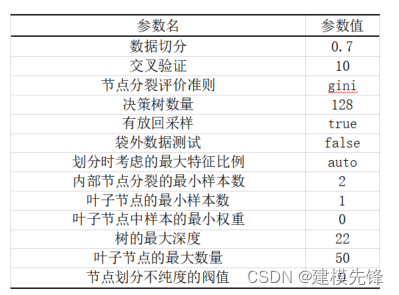
2.4 模型训练与分类
model = RandomForestClassifier(n_estimators=128,max_depth=22,random_state=1) # min_samples_leaf=11
model.fit(X_train,Y_train)
score = model.score(X_test,Y_test)
print('模型分数:',score)
# 计算在训练集和测试集上的预测均方根误差
model_lab = model.predict(X_train)
model_pre = model.predict(X_test)
train_mse = mean_squared_error(Y_train,model_lab)
test_mse = mean_squared_error(Y_test,model_pre)
print('训练数据集上的均方根误差:',train_mse)
print('测试数据集上的均方根误差:',test_mse)
# 模型使用与评估
y_pred = model.predict(X_test)
print("准确率: %.3f" % accuracy_score(Y_test, y_pred))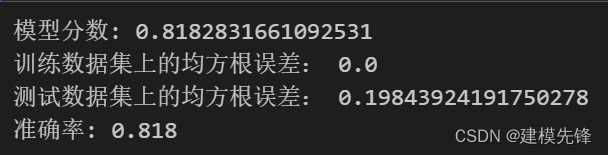
3模型评估
3.1 模型评估结果


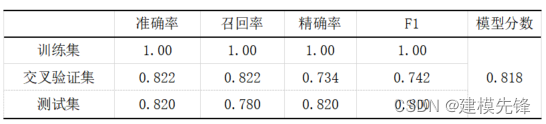
模型评估结果如表所示,表中展示了训练集和测试集的分类评价指标,通过量化指标来衡量随机森林对训练、测试数据的分类效果。准确率:预测正确样本占总样本的比例,准确率越大越好;召回率:实际为正样本的结果中,预测为正样本的比例,召回率越大越好;精确率:预测出来为正样本的结果中,实际为正样本的比例,精确率越大越好;F1:精确率和召回率的调和平均,精确率和召回率是互相影响的,虽然两者都高是一种期望的理想情况,然而实际中常常是精确率高、召回率就低,或者召回率低、但精确率高。若需要兼顾两者,那么就可以用F1指标。随机森林的精确率较高。随机森林分类模型分数结果为0.818.
3.2 混淆矩阵
# 混淆矩阵
from sklearn.metrics import confusion_matrix
import matplotlib.ticker as ticker
cm = confusion_matrix(Y_test, y_pred,labels=[0,1,-1])
print('混淆矩阵:\n', cm)
labels=['-1','0','1']
from sklearn.metrics import ConfusionMatrixDisplay
cm_display = ConfusionMatrixDisplay(cm,display_labels=labels).plot()以热力图的形式展示了随机森林分类模型结果的混淆矩阵

3.3 绘制房价类别三分类的ROC曲线和AUC数值

模型ROC曲线和AUC数值如图16所示,图16中的橙色线为参考,即在不使用模型的情况下,Sensitivity 和1-Specificity之比恒等于1。通过绘制ROC曲线,重要的是计算折线下的面积,即图中的阴影部分,这个面积称为AUC。在做模型评估时,希望AUC的值越大越好,通常情况下,当AUC在0.8以上时,模型就基本可以接受了。在AUC>0.5的情况下,AUC越接近于1,说明模型效果越好;AUC在 0.5~0.7时有较低准确性,AUC在0.7~0.9时有一定准确性,AUC在0.9以上时有较高准确性;AUC=0.5时,跟随机猜测一样,模型没有分类价值;AUC<0.5时,比随机猜测还差。然而随机森林分类模型三种分类的AUC值都在0.90以上,说明模型分类效果明显,有较高准确性。
3.4 特征重要性可视化
features = X.columns
importances = model.feature_importances_
df = pd.DataFrame()
df['特征'] = features
df['重要性'] = importances
df = df.sort_values('重要性',ascending=False)
# df.iloc[2,1] = df.iloc[2,1]+0.2
xx = df['特征']
yy = df['重要性']
colors = ['darkgreen','gold','red','navy','orange','lime','plum','sienna']
plt.figure(figsize=(15,5))
plt.barh(xx,yy,0.4,color=colors,alpha=0.8)#color参数传入颜色列表,可以在一幅图中显示不同颜色
plt.xlabel('Importance score')
plt.ylabel('variable')
plt.title('RandomForestRegressor')
plt.grid()
plt.show()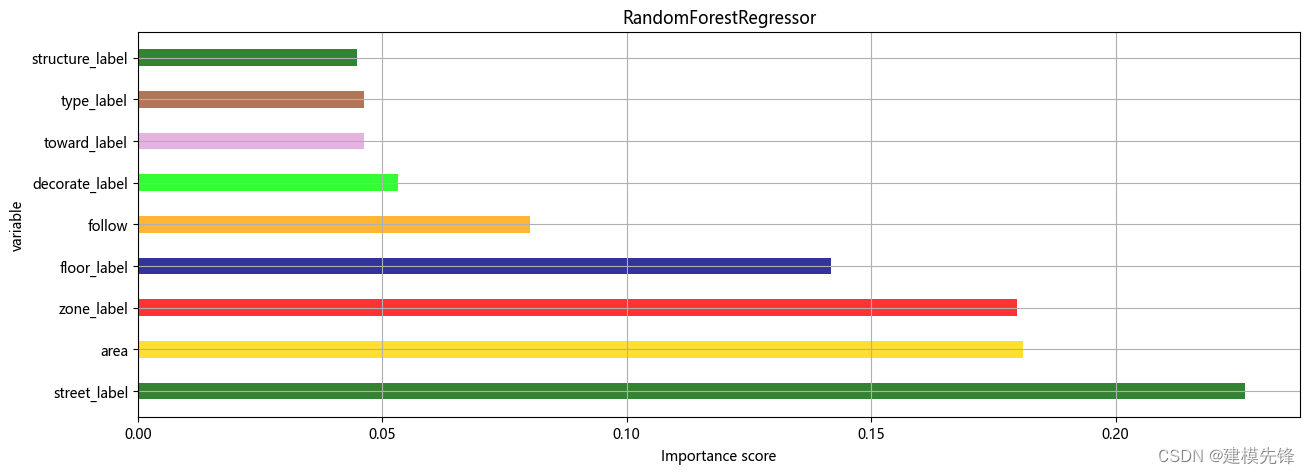
分类标签对房价的影响中,街道位置对房价的影响重要性最大,区域和建造面积重要性其次,相比较,房子的构造和户型以及房子朝向对房价的影响重要性较小,装修、关注度以及楼层层次对房价的影响重要性适中。
总结
通过对宜昌市二手房数据的分析,我们探讨了影响房价的重要因素,并对房价进行分类,熟悉了python中numpy和pandas等高级数据处理包的应用,并掌握了数据分析的步骤和流程。经过机器学习中对随机森林模型的研究,进一步加深了对机器学习的了解,熟悉了随机森林模型的原理和在python中的使用方法,并加深了对机器学习模型常用评价指标的了解,每种算法都有其各自的优点和使用场景,没有最好的算法,只有更好的数据。
参考资料
[1]李超.机器学习模型在股票价格时间序列分析中的应用与比较[J].电子世界,2021(09):66-70.
[2]李岩. 基于随机森林的沪深300预测研究[J]. 品牌研究,2022(2):108-110.
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!