C++进阶学习：map和set的实现

我们知道set和map的底层其实是红黑树，在学习完红黑树这个数据结构之后，我们开始简单模拟实现一下这两个STL容器

目录

1.set和map的泛型编程思想

2.红黑树的结构??

2.1.迭代器的实现? ? ??

2.2.迭代器的 operator++

2.3.迭代器的代码?

2.4.set和map迭代器

?2.4.1.Insert的代码

2.4.2迭代器结构

??3.代码实现

3.1. set.h

3.2. map.h

3.3. RBTree.h

---

1.set和map的泛型编程思想

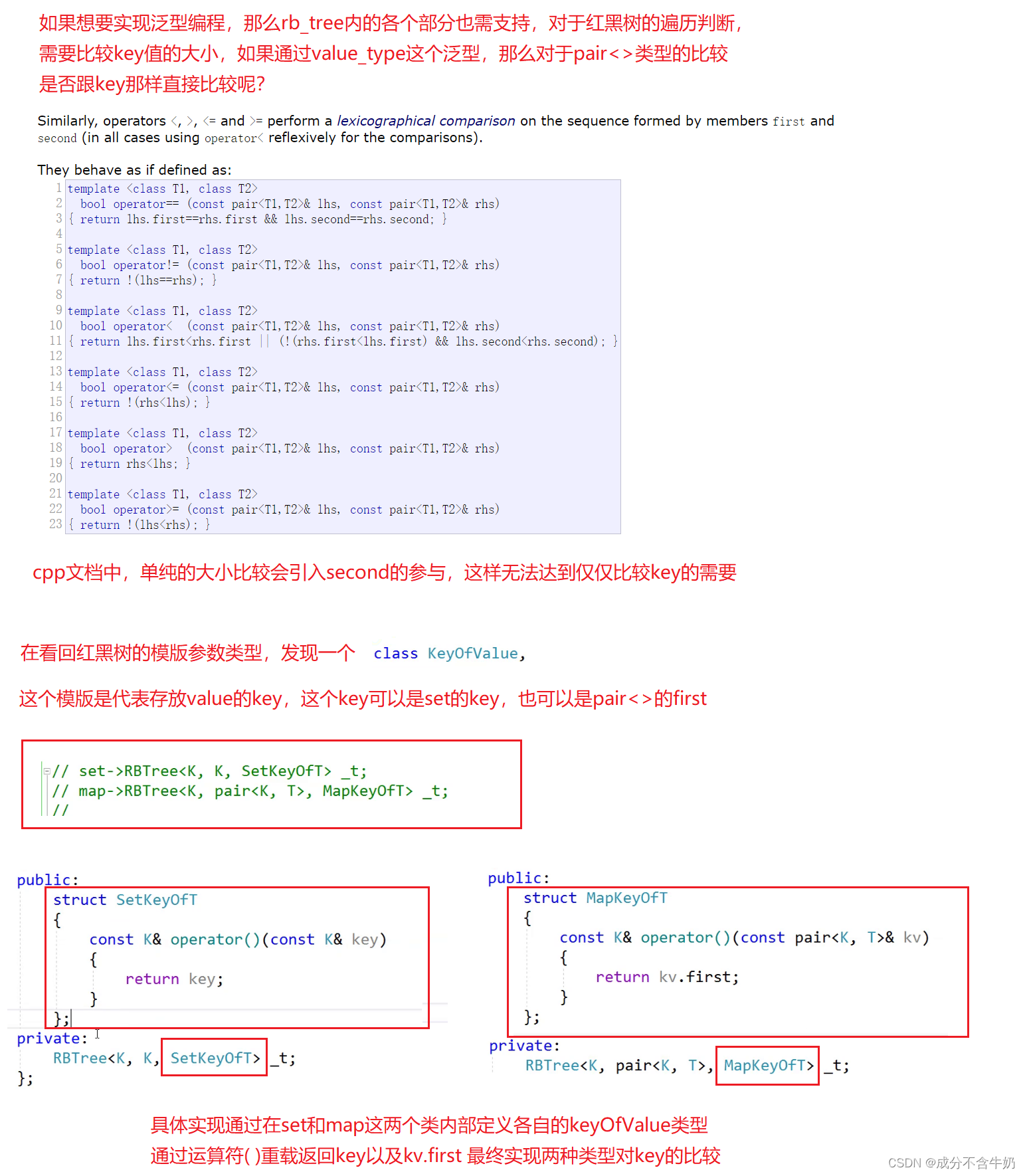
因为set和map底层高度封装所以我们需要通过源码的阅读来确定大致框架，我们发现map和set的内部均有一个value_type类型，其可以是key也可以是pair<>简化一下上图，我们大致定义出set和map?

我们知道泛型编程的核心就是代码的复用，在这一章节体现在同一个RBTree.h文件可以支持mySet.h和myMap.h随时用?

? 而我们在前面红黑树的学习过程中，对于insert的插入位置查找，以及find的数据位置查找都需要遍历树的分支，通过的是key来寻找，如果是set类型就直接寻找，但是如果是pair类型呢？我们可能会说那就是pair<>.first来实现就好了！这个回答是没有问题的，结果却是形成了两棵树或者是需要重载两个insert，一个为bool insert(const K& key)，另一个为bool insert(const pair<K, V>& kv)??，这样无法较好泛型编程思想

2.红黑树的结构??

通过上部分的泛型编程，讲述我们在红黑树的中定义了一个新的变量KeyOfValue来实现这个对应set与map的匹配，又因为在C++学习进阶：set 和 map-CSDN博客中关于【】重载部分，我们知道了insert返回的是pair<iterator, bool>类型，所以我们开始定义迭代器！

2.1.迭代器的实现? ? ??

首先迭代器是一个类似于指针的容器（本质是指针），内部存放节点，那么底层实现也是通过树的节点，并且为了实现const_iterator，需要传入多个模版参数，因为之前我们在list章节，讲过迭代器的实现这里的话就不赘述了，就大概展示一下结构组分

2.2.迭代器的 operator++

++和--这两个操作符重载均是为了通过迭代器进行节点的遍历，而根据红黑树的规律，以及STL库中set和map迭代器遍历规律，我们需要将节点通过正向or负向中序遍历的方式来实现！

2.3.迭代器的代码?

template<class V, class Ref, class Ptr>
struct Tree_iterator
{
	typedef Tree_iterator<V, Ref, Ptr> Self;
	typedef RBTreeNode<V> Node;

	Node* _node = nullptr;

	Tree_iterator(Node* node)
		:_node(node)
	{}
	// 实现const的拷贝构造
	Tree_iterator(const Tree_iterator<V, V&, V*>& it)
		:_node(it._node)
	{}

	Self& operator=(const Self& s)
	{
		_node = s._node;
		return *this;
	}
	Self& operator++()
	{
		// 右子树不为空，遍历到最左节点
		if (_node->_right != nullptr)
		{
			Node* current = _node->_right;
			while (current != nullptr && current->_left != nullptr)
				current = current->_left;
			_node = current;
		}
		// 右子树为空 大的节点在祖先处
		else
		{
			Node* current = _node;
			Node* parent = current->_parent;
			// 如果current在parent的右进入循环，下一个节点就是祖父节点
			while (parent != nullptr && current == parent->_right)
			{
				current = parent;
				parent = parent->_parent;
			}
			// 如果current是parent的左，不进入循环，下一个节点就是父亲节点
			_node = parent;
		}

		return *this;
	}
	Self& operator--()
	{
		if (_node->_left != nullptr)
		{
			Node* current = _node->_left;
			while (current != nullptr && current->_right != nullptr)
				current = current->_right;
			_node = current;
		}
		else
		{
			Node* current = _node;
			Node* parent = current->_parent;
			while (parent != nullptr && current == parent->_left)
			{
				current = parent;
				parent = parent->_parent;
			}
			_node = parent;
		}
		return *this;
	}

	bool operator!=(const Self& s) { return _node != s._node; }
	bool operator==(const Self& s) { return _node == s._node; }


	Ref operator*() { return _node->_value; }
	Ptr operator->() { return &_node->_value; }
};

2.4.set和map迭代器

实现完红黑树迭代器后我们开始实现set和map的迭代器，我们知道红黑树需要同时兼容set和map，而set是key类型并且key不能修改，map是pair<const Key, value>类型?，这两个在实现时，set的迭代器不支持修改，而map的迭代器不支持key修改但是支持Value修改

?2.4.1.Insert的代码

// 增查
	pair<iterator, bool> insert(const V& value)
	{
		// 1.先插入节点

		if (_root == nullptr)
		{
			_root = new Node(value);
			// 根节点默认为黑色
			_root->_col = BLACK;
			return make_pair(iterator(_root), true);
		}

		Node* parent = nullptr;
		Node* current = _root;

		while (current != nullptr)
		{

			parent = current;

			if (kov(current->_value) < kov(value))
				current = current->_right;
			else if (kov(current->_value) > kov(value))
				current = current->_left;
			else
				return make_pair(iterator(current), false);
		}

		Node* newNode = new Node(value);
		current = newNode;
		// 新增节点默认为红色
		current->_col = RED;

		// 通过大小插入左右
		if (kov(parent->_value) < kov(value))
			parent->_right = current;
		else
			parent->_left = current;

		current->_parent = parent;


		// 2.实现颜色的变换  情况来回的迭代直至不满足循环 退出时就满足了红黑树
		while (parent != nullptr && parent->_col == RED)
		{
			/*进入循环情况：同时满足父节点不为空，且为红色
			  原因： 如果父节点为空，则current为_root
					如果父节点为黑色，就不用更新颜色了*/

			Node* grandparent = parent->_parent;

			// 找到叔叔节点位置
			if (parent == grandparent->_left)
			{
				// uncle在父亲右边
				Node* uncle = grandparent->_right;

				// 情况一：叔叔存在，且叔叔为红色
				if (uncle != nullptr && uncle->_col == RED)
				{
					parent->_col = uncle->_col = BLACK;
					grandparent->_col = RED;
					// 继续向上调整
					current = grandparent;
					parent = current->_parent;
				}
				// 情况二：叔叔不存在 或者 叔叔存在但是颜色为黑色
				else
				{

					if (current == parent->_left)
					{
						RotateR(grandparent);
						parent->_col = BLACK;
						grandparent->_col = RED;
					}
					// current在右边
					else
					{
						RotateL(parent);
						RotateR(grandparent);
						// 通过旋转后，旋转内部就已经完成了指针的指向
						current->_col = BLACK;
						grandparent->_col = RED;

					}
					// 直接退出循环即可，也可以不退出，因为父亲已经为黑色了
					break;
				}
			}

			else
			{
				// uncle在父亲左边
				Node* uncle = grandparent->_left;
				if (uncle != nullptr && uncle->_col == RED)
				{
					parent->_col = uncle->_col = BLACK;
					grandparent->_col = RED;
					// 继续向上调整
					current = grandparent;
					parent = current->_parent;
				}
				else
				{
					if (current == parent->_right)
					{
						RotateL(grandparent);
						parent->_col = BLACK;
						grandparent->_col = RED;
					}
					// current在左边
					else {
						// 注意这里单旋的节点不同
						RotateR(parent);
						RotateL(grandparent);
						grandparent->_col = RED;
						current->_col = BLACK;
					}

					break;
				}
			}
		}
		// 保持根节点始终为黑色，当current到达根节点可能为RED，这里就在外部变黑
		_root->_col = BLACK;
		return make_pair(iterator(newNode), true);

	}

?所以我们实现set和map时也需要按照这个规律，这里我们以set为例子，结合insert为pair<iterator, bool>类型的函数?

2.4.2迭代器结构

set的迭代器结构

这样子我们应该是实现了const_iterator的作用，那我们通过插入数据来判断一下?，插入是成功的，不过最终会出现报错

如下图所示

那如何解决呢？

法一：

我们知道这里是，普通类型的迭代器不能作为const_iterator的接收值，也就是类型无法匹配，那么我们可以通过类型的拷贝构造，将const_iterator可以转化为原生的iterator迭代器，这样子iterator既可以作为普通的迭代器，也可以实现为const_iterator，带着这样的想法我们实现一个拷贝构造函数，代码在2.3.处有样例

法二：

另外，我们在研究pair类型时，发现pair也通过法一类似的方法实现了一个拷贝构造函数，也就是我们可以通过其他类型来实现const_iterator，我们知道迭代器的本质就是一个节点的指针，那么Node* 转化为const_iterator理论上是可行的，在通过iterator的( )默认构造函数，就可以通过iterator(pointer)

有了set的迭代器为例子，以及insert的实现，我们现在开始实现map的迭代器，map和set主要不同就是，map支持普通迭代器修改，但是会限制key的修改，也就是我们不能像set一样锁死map?

map的迭代器

我们在测试用例中尝试修改key，发现会出错，而value不受影响

?3.代码实现

3.1. set.h

#pragma once
#include<iostream>
#include "RBTree.h"
using namespace std;

namespace zhong
{
	// set的实现
	template<class V>
	class set
	{
		// 类型匹配 对应树的 class keyOfValue
		struct SetKetOf
		{
			const V& operator()(const V& value_type) { return value_type; }	// 通过定义keyOfValue kov 然后 借助()重载 来 找到key
		};

	public:
		// 这里体现了typename的作用
		// 对类模板取内嵌类型，需要加typename告知编译器这里是内嵌类型
		typedef typename RBTree<V, V, SetKetOf>::const_iterator iterator;
		typedef typename RBTree<V, V, SetKetOf>::const_iterator const_iterator;

		
		// 迭代器
		iterator begin() const { return _tree.begin(); }
		iterator end() const { return _tree.end(); }
		
		// 增查
		pair<iterator, bool> insert(const V& value) { return _tree.insert(value); }
		// iterator find(const V& value) { return _tree.find(value); }


	private:
		RBTree<V, V, SetKetOf> _tree;
	};

	void test_set1()
	{
		set<int> s1;
		s1.insert(2);
		s1.insert(3);
		s1.insert(4);
		s1.insert(1);
		set<int>::iterator it = s1.begin();
		
		while (it != s1.end())
		{
			// *it = 10;
			cout << *it << " ";
			++it;
		}
		cout << endl;

	}
}

3.2. map.h

#pragma once
#include<map>
#include<iostream>
#include"RBTree.h"
using namespace std;


namespace zhong
{
	template<class K, class V>
	class map
	{
		struct MapKetOf
		{
			// 通过定义keyOfValue kov 然后 借助()重载 来 找到pair的first

			const K& operator()(const pair<K, V>& value_type) { return value_type.first; }
		};
	public:
		// 这里体现了typename的作用
	// 对类模板取内嵌类型，需要加typename告知编译器这里是内嵌类型
		typedef typename RBTree<K, pair<const K, V>, MapKetOf>::iterator iterator;
		typedef typename RBTree<K, pair<const K, V>, MapKetOf>::const_iterator const_iterator;
	
		V& operator[]    (const K& key)
		{
			// insert返回pair<iterator, bool>，用ret接收插入节点的迭代器，解引用找到这个节点，接着 . 找到second
			iterator ret = _tree.insert(make_pair(key, V())).first;
			return (*ret).second;

			//pair<iterator, bool> ret = insert(make_pair(key, V()));
			// return ret.first->second;
		}

		// 迭代器
		iterator begin() { return _tree.begin(); }
		iterator end() { return _tree.end(); }

		pair<iterator, bool> insert(const pair<K, V>& value_type) { return _tree.insert(value_type); }


	private:
		RBTree<K, pair<const K, V>, MapKetOf> _tree;
	};

	void test_map1()
	{

		map<string, string> dict;
		dict.insert(make_pair("name", "zhong"));
		dict.insert(make_pair("age", "21"));
		dict.insert(make_pair("id", "2022044026"));

		map<string, string>::iterator it = dict.begin();
		while (it != dict.end())
		{

			cout << (*it).first << " " << (*it).second << endl;
			++it;
		}

	}
	void test_map2()
	{
		// 测试map中的[]

		string str[] = { "嗯","哦","噢","喔","好","噢","噢","好" };
		map<string, int> countMap;

		for (auto& s : str)
		{

			// map中实现计数要求
			// 借助[]重载实现
			countMap[s]++;
			// 分成多样的功能
		}

		map<string, int>::iterator ret = countMap.begin();
		while (ret != countMap.end())
		{
	
			cout << (*ret).first << " " << (*ret).second << endl;
			++ret;
		}

	}
}

3.3. RBTree.h

#include<iostream>
#include<vector>
using namespace std;

// 实现颜色
enum Colour
{
	RED,
	BLACK
};

template<class V>
struct RBTreeNode
{
	// 三叉链结构
	RBTreeNode<V>* _left;
	RBTreeNode<V>* _right;
	RBTreeNode<V>* _parent;

	V _value;
	// 实现颜色
	Colour _col;

	RBTreeNode(const V& value)
		: _left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _value(value)
		, _col(RED)	// 默认新节点红色 根节点为黑
	{}
};

template<class V, class Ref, class Ptr>
struct Tree_iterator
{
	typedef Tree_iterator<V, Ref, Ptr> Self;
	typedef RBTreeNode<V> Node;

	Node* _node = nullptr;

	Tree_iterator(Node* node)
		:_node(node)
	{}
	// 实现const的拷贝构造
	Tree_iterator(const Tree_iterator<V, V&, V*>& it)
		:_node(it._node)
	{}

	Self& operator=(const Self& s)
	{
		_node = s._node;
		return *this;
	}
	Self& operator++()
	{
		// 右子树不为空，遍历到最左节点
		if (_node->_right != nullptr)
		{
			Node* current = _node->_right;
			while (current != nullptr && current->_left != nullptr)
				current = current->_left;
			_node = current;
		}
		// 右子树为空 大的节点在祖先处
		else
		{
			Node* current = _node;
			Node* parent = current->_parent;
			// 如果current在parent的右进入循环，下一个节点就是祖父节点
			while (parent != nullptr && current == parent->_right)
			{
				current = parent;
				parent = parent->_parent;
			}
			// 如果current是parent的左，不进入循环，下一个节点就是父亲节点
			_node = parent;
		}

		return *this;
	}
	Self& operator--()
	{
		if (_node->_left != nullptr)
		{
			Node* current = _node->_left;
			while (current != nullptr && current->_right != nullptr)
				current = current->_right;
			_node = current;
		}
		else
		{
			Node* current = _node;
			Node* parent = current->_parent;
			while (parent != nullptr && current == parent->_left)
			{
				current = parent;
				parent = parent->_parent;
			}
			_node = parent;
		}
		return *this;
	}

	bool operator!=(const Self& s) { return _node != s._node; }
	bool operator==(const Self& s) { return _node == s._node; }


	Ref operator*() { return _node->_value; }
	Ptr operator->() { return &_node->_value; }
};


template<class K, class V, class keyOfValue>
class RBTree
{
	typedef RBTreeNode<V> Node;
public:
	typedef Tree_iterator<V, V&, V*> iterator;
	typedef Tree_iterator<V, const V&, const V*> const_iterator;


	// 迭代器
	iterator begin()
	{
		Node* current = _root;
		while (current != nullptr && current->_left != nullptr)
			current = current->_left;

		return iterator(current);
	}
	iterator end()
	{
		return iterator(nullptr);
	}
	const_iterator begin() const
	{
		Node* current = _root;
		while (current != nullptr && current->_left != nullptr)
			current = current->_left;

		return const_iterator(current);
	}
	const_iterator end() const
	{
		return const_iterator(nullptr);
	}

	// 增查
	pair<iterator, bool> insert(const V& value)
	{
		// 1.先插入节点

		if (_root == nullptr)
		{
			_root = new Node(value);
			// 根节点默认为黑色
			_root->_col = BLACK;
			return make_pair(iterator(_root), true);
		}

		Node* parent = nullptr;
		Node* current = _root;

		while (current != nullptr)
		{

			parent = current;

			if (kov(current->_value) < kov(value))
				current = current->_right;
			else if (kov(current->_value) > kov(value))
				current = current->_left;
			else
				return make_pair(iterator(current), false);
		}

		Node* newNode = new Node(value);
		current = newNode;
		// 新增节点默认为红色
		current->_col = RED;

		// 通过大小插入左右
		if (kov(parent->_value) < kov(value))
			parent->_right = current;
		else
			parent->_left = current;

		current->_parent = parent;


		// 2.实现颜色的变换  情况来回的迭代直至不满足循环 退出时就满足了红黑树
		while (parent != nullptr && parent->_col == RED)
		{
			/*进入循环情况：同时满足父节点不为空，且为红色
			  原因： 如果父节点为空，则current为_root
					如果父节点为黑色，就不用更新颜色了*/

			Node* grandparent = parent->_parent;

			// 找到叔叔节点位置
			if (parent == grandparent->_left)
			{
				// uncle在父亲右边
				Node* uncle = grandparent->_right;

				// 情况一：叔叔存在，且叔叔为红色
				if (uncle != nullptr && uncle->_col == RED)
				{
					parent->_col = uncle->_col = BLACK;
					grandparent->_col = RED;
					// 继续向上调整
					current = grandparent;
					parent = current->_parent;
				}
				// 情况二：叔叔不存在 或者 叔叔存在但是颜色为黑色
				else
				{

					if (current == parent->_left)
					{
						RotateR(grandparent);
						parent->_col = BLACK;
						grandparent->_col = RED;
					}
					// current在右边
					else
					{
						RotateL(parent);
						RotateR(grandparent);
						// 通过旋转后，旋转内部就已经完成了指针的指向
						current->_col = BLACK;
						grandparent->_col = RED;

					}
					// 直接退出循环即可，也可以不退出，因为父亲已经为黑色了
					break;
				}
			}

			else
			{
				// uncle在父亲左边
				Node* uncle = grandparent->_left;
				if (uncle != nullptr && uncle->_col == RED)
				{
					parent->_col = uncle->_col = BLACK;
					grandparent->_col = RED;
					// 继续向上调整
					current = grandparent;
					parent = current->_parent;
				}
				else
				{
					if (current == parent->_right)
					{
						RotateL(grandparent);
						parent->_col = BLACK;
						grandparent->_col = RED;
					}
					// current在左边
					else {
						// 注意这里单旋的节点不同
						RotateR(parent);
						RotateL(grandparent);
						grandparent->_col = RED;
						current->_col = BLACK;
					}

					break;
				}
			}
		}
		// 保持根节点始终为黑色，当current到达根节点可能为RED，这里就在外部变黑
		_root->_col = BLACK;
		return make_pair(iterator(newNode), true);

	}
	iterator find(const K& key)
	{

	}


	// 外部调用封装函数

	// 中序遍历
	void inOrder() { _inOrder(_root); cout << endl; }
	// 判断是否平衡
	bool ifBalance()
	{
		if (_root == nullptr)
			return true;

		if (_root->_col == RED)
			return false;
		// 作为辅助判断
		int flag = 0;
		Node* current = _root;

		while (current != nullptr)
		{
			if (current->_col == BLACK)
				flag++;
			current = current->_left;
		}
		// 设置一个flag值记录某一条路径的长度
		// 如果flag不等于任何一条路径的长度就表示某一条路径黑色节点数有误

		cout << "flag大小为：" << flag << endl;
		// 根节点到当前节点路径上黑色节点数量
		int blackNum = 0;
		return check(_root, blackNum, flag);
	}
	// 返回树节点个数
	int size() { return _size(_root); }
	// 返回树的高度
	int Height() { return _Height(_root); }


	// 封装函数区	
private:
	// 左单旋
	void RotateL(Node* root)
	{
		Node* parent = root;
		Node* subR = parent->_right;
		Node* subRL = subR->_left;
		Node* grandparent = parent->_parent;

		subR->_left = parent;
		parent->_right = subRL;

		if (subRL != nullptr)
			subRL->_parent = parent;

		parent->_parent = subR;
		parent = subR;

		if (grandparent == nullptr)
		{
			_root = parent;
		}
		else
		{
			if (grandparent->_left == root)
				grandparent->_left = parent;
			else
				grandparent->_right = parent;
		}
		parent->_parent = grandparent;

	}
	// 右单旋
	void RotateR(Node* root)
	{
		Node* parent = root;
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
		Node* grandparent = parent->_parent;

		subL->_right = parent;
		parent->_left = subLR;

		if (subLR != nullptr)
		{
			subLR->_parent = parent;
		}
		parent->_parent = subL;
		parent = subL;

		if (grandparent == nullptr)
		{
			_root = parent;
		}
		else
		{
			if (grandparent->_left == root)
				grandparent->_left = parent;
			else
				grandparent->_right = parent;
		}
		parent->_parent = grandparent;

	}
	// 中序遍历
	void _inOrder(Node* root)
	{
		keyOfValue kov;
		if (root == nullptr)
			return;

		_inOrder(root->_left);
		cout << kov(root->_value) << " ";
		_inOrder(root->_right);
	}
	// 检查是否出现连续红色节点
	bool check(Node* root, int blackNum, const int flag)
	{
		if (root == nullptr)
		{
			// cout << "黑色节点数目：" << blackNum << endl;

			if (blackNum != flag)
			{
				cout << "路径上的黑色节点数存在不同" << endl;
				return false;
			}

			return true;
		}

		if (root->_col == RED && root->_parent->_col == RED)
		{
			// 子节点和父节点均为红色，不符合红黑树
			cout << "存在连续的红色节点" << endl;
			return false;
		}
		if (root->_col == BLACK)
			++blackNum;

		// 传值调用，只影响函数块，上一层不影响下一层
		return check(root->_left, blackNum, flag) && check(root->_right, blackNum, flag);
	}
	// 计算树的节点个数
	int _size(Node* root)
	{
		if (root == nullptr)
			return 0;

		return _size(root->_left) + _size(root->_right) + 1;
	}
	// 计算树的高度
	int _Height(Node* root)
	{
		if (root == nullptr)
			return 0;

		int leftHeight = _Height(root->_left);
		int rightHeight = _Height(root->_right);

		return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;

	}

private:

	Node* _root = nullptr;
	keyOfValue kov;
};

到了这里通过红黑树初步封装map和set就讲到这里了，我们再来讲一下什么是封装，封装本质就是套个盒子在外面，当我们研究封装好的某一个类时，我们需要逐层剖析，找到封装前到底是什么牛鬼蛇神，进而有助于我们阅读源码

封装是面向对象编程中的一种重要特性，它指的是将对象的状态信息隐藏在对象内部，不允许外部程序直接访问对象内部的信息，而是通过该类所提供的方法来实现对内部信息的操作和访问。封装可以有效地保护对象的数据安全性，同时也可以提高代码的可维护性和可重用性。