Leetcode热题之二分搜索

模板

这个系列的题可以说是秒掉，只要记住这个模板，同时要理解边界问题就好了.如果你要找左节点，mid就是l + r >> 1,如果你要找右节点，那么mid就是l + r + 1 >> 1,因为除于2的时候会四舍五入。我给的模板是找左节点的

int l = 0 , r = nums.length - 1;  
while(l < r) {  
    int mid = l + r >> 1;  
    if(target <= nums[mid]) r = mid;  
    else l = mid + 1;  
}

Leetcode原题代码

35搜索查找位置

题目

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

请必须使用时间复杂度为 O(log n) 的算法。

示例 1:

输入: nums = [1,3,5,6], target = 5
输出: 2

代码

class Solution {
    public int searchInsert(int[] nums, int target) {
        int n = nums.length;
        int l = 0, r = n - 1, f = -1;
        while(l < r) {
            int mid = l + r >> 1;
            if(nums[mid] >= target) r = mid;
            else l = mid + 1;  
        }
        if(nums[l] == target)   return l;
        else if(nums[l] < target)   return r + 1;
        else return r;
    }
}

74搜索二维矩阵

题目

给你一个满足下述两条属性的 m x n 整数矩阵：

• 每行中的整数从左到右按非严格递增顺序排列。
• 每行的第一个整数大于前一行的最后一个整数。
  给你一个整数 target ，如果 target 在矩阵中，返回 true ；否则，返回 false 。
  示例 1：

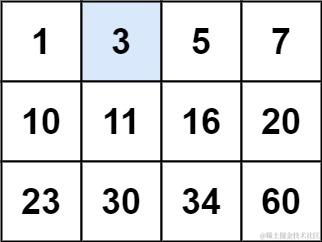
输入： matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
输出： true

代码

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int n = matrix.length;
        int m = matrix[0].length;
        int idx = 0;
        int[] nums = new int[n * m];
        for(int i = 0;i < n;i ++) {
            for(int j = 0;j < m;j ++){
                nums[idx ++] = matrix[i][j];
            }
        }
        int l = 0 , r = n * m - 1;
        while(l < r) {
            int mid = l + r >> 1;
            if(target <= nums[mid])    r = mid;
            else l = mid + 1;
        }
        if(nums[l] == target)   return true;
        else return false;
    }
}

34 在排序数组中查找元素的第一个和最后一个位置

题目

给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。

示例 1：

输入： nums = [5,7,7,8,8,10], target = 8
输出： [3,4]

代码

class Solution {
    public int[] searchRange(int[] nums, int target) {
        int n = nums.length;
        if(n == 0)  return new int[]{-1, -1};
        int l = 0, r = n - 1;
        while(l < r) {
            int mid = l + r >> 1;
            if(nums[mid] >= target) r = mid;
            else l = mid + 1;
        }
        System.out.println(l);
        if(nums[l] != target) return new int[]{-1, -1};
        else r = n - 1;
        int[] ans = new int[2];
        ans[0] = l;
        while(l < r) {
            int mid = l + r + 1>> 1;
            if(nums[mid] <= target) l = mid;
            else r = mid - 1;
        }
        ans[1] = r;
        return ans;
    }
}

33 搜索旋转排序数组

题目

整数数组 nums 按升序排列，数组中的值 互不相同 。

在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 旋转，使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。

给你 旋转后 的数组 nums 和一个整数 target ，如果 nums 中存在这个目标值 target ，则返回它的下标，否则返回 -1 。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

示例 1：

输入： nums = [4,5,6,7,0,1,2], target = 0
输出： 4

代码

class Solution {
    public int search(int[] nums, int target) {
        int n = nums.length;
        if (n == 1) {
            if (target == nums[0]) return 0; // 如果数组长度为1且目标值与唯一元素相等，返回0
            else return -1; // 否则返回-1，表示未找到目标值
        }

        int rever = 0;
        // 找到旋转点的索引
        for (int i = 1; i < n; i++) {
            if (nums[i] < nums[i - 1]) {
                rever = i;
            }
        }

        int l = 0, r;
        // 根据旋转点的位置设置右边界
        if (rever != 0) {
            r = rever - 1;
        } else {
            r = n - 1;
        }

        // 在前半段查找目标值
        while (l < r) {
            int mid = l + r >> 1;
            if (nums[mid] >= target) r = mid;
            else l = mid + 1;
        }

        // 检查是否找到目标值
        if (target > nums[l]) return -1;
        else if (target == nums[l]) return l;

        // 在后半段查找目标值
        l = rever;
        r = n - 1;
        while (l < r) {
            int mid = l + r >> 1;
            if (nums[mid] >= target) r = mid;
            else l = mid + 1;
        }

        // 返回目标值的索引，如果未找到则返回-1
        if (target == nums[l]) return l;
        else return -1;
    }
}

153 寻找旋转排序数组中的最小值

题目

已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次 旋转 后，得到输入数组。例如，原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到：

• 若旋转 4 次，则可以得到 [4,5,6,7,0,1,2]
• 若旋转 7 次，则可以得到 [0,1,2,4,5,6,7]

注意，数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。

给你一个元素值 互不相同 的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

示例 1：

输入： nums = [3,4,5,1,2]
输出： 1
解释： 原数组为 [1,2,3,4,5] ，旋转 3 次得到输入数组。

代码

class Solution {
    public int findMin(int[] nums) {
        int n = nums.length;
        int l = 0, r = n - 1;
        if(nums[r] >= nums[l])  return nums[l];
        while(l < r) {
            int mid = l + r>> 1;
            if(nums[mid] > nums[r])    l = mid + 1;
            else r = mid;
        }
        return nums[l];
    }
}

4 寻找两个正序数组的中位数

题目

给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。

算法的时间复杂度应该为 O(log (m+n)) 。

示例 1：

输入： nums1 = [1,3], nums2 = [2]
输出： 2.00000
解释： 合并数组 = [1,2,3] ，中位数 2

代码

解法一比较简洁的迭代去二分搜索，每一次去掉K/2个元素

class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int n = nums1.length;
        int m = nums2.length;
        // 把求中位数转换成求第k小的数了
        int left = (n + m + 1) / 2;
        int right = (n + m + 2) / 2;
        return (getKth(nums1, 0, n - 1, nums2, 0, m - 1, left) + getKth(nums1, 0, n - 1, nums2, 0, m - 1, right)) * 0.5;
    }
    public int getKth(int[] nums1, int start1, int end1, int[] nums2, int start2, int end2, int k) {
        int len1 = end1 - start1 + 1;
        int len2 = end2 - start2 + 1;

        if(len1 > len2) return getKth(nums2, start2, end2, nums1,start1,end1,k);
        if(len1 == 0)   return nums2[start2 + k - 1];

        if(k == 1)  return Math.min(nums1[start1], nums2[start2]);

        int i = start1 + Math.min(len1, k / 2) - 1;
        int j = start2 + Math.min(len2, k / 2) - 1;

        if(nums1[i] > nums2[j]) {
            return getKth(nums1, start1, end1, nums2, j + 1, end2, k - (j -start2 + 1));
        } else {
             return getKth(nums1, i + 1, end1, nums2, start2, end2, k - (i -start1 + 1));
        }
    }
}

解法二：代码有点冗余，但易于理解。解法一二思路都是一样的

class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int m = nums1.length;
        int n = nums2.length;

        // 确保 nums1 的长度小于等于 nums2 的长度
        if (m > n) {
            int[] temp = nums1;
            nums1 = nums2;
            nums2 = temp;
            int tmp = m;
            m = n;
            n = tmp;
        }

        int iMin = 0, iMax = m, halfLen = (m + n + 1) / 2;
        while (iMin <= iMax) {
            int i = (iMin + iMax) / 2;
            int j = halfLen - i;

            // 寻找正确的划分点，确保左侧元素小于右侧元素
            if (i < iMax && nums2[j - 1] > nums1[i]) {
                // i 太小，需要增大
                iMin = i + 1;
            } else if (i > iMin && nums1[i - 1] > nums2[j]) {
                // i 太大，需要减小
                iMax = i - 1;
            } else {
                // 找到正确的划分点

                // 计算左侧划分的最大值
                int maxLeft = 0;
                if (i == 0) {
                    maxLeft = nums2[j - 1];
                } else if (j == 0) {
                    maxLeft = nums1[i - 1];
                } else {
                    maxLeft = Math.max(nums1[i - 1], nums2[j - 1]);
                }

                // 如果总长度为奇数，返回左侧最大值作为中位数
                if ((m + n) % 2 == 1) {
                    return maxLeft;
                }

                // 计算右侧划分的最小值
                int minRight = 0;
                if (i == m) {
                    minRight = nums2[j];
                } else if (j == n) {
                    minRight = nums1[i];
                } else {
                    minRight = Math.min(nums1[i], nums2[j]);
                }

                // 如果总长度为偶数，返回左侧最大值和右侧最小值的平均值作为中位数
                return (maxLeft + minRight) / 2.0;
            }
        }
        return 0.0;
    }
}