二叉树的遍历
二叉树三种遍历方式简介:
二叉树的遍历:
目的:得到树所有节点的一个线性排列
用途:是树结构插入,删除,修改,查找和排序运算的前提,是二叉树一切运算的基础和核心
(主要)遍历方法:
DLR(先访问根节点,再遍历左子树,再遍历右子树):先(根)序遍历,左子树和右子树的遍历和先序遍历一致,即先访问左子树的根节点,再按先序遍历依次查询,右子树也一样。一下遍历方式同理。得到的表达式为前缀表示
例:

顺序为ABDECF
具体的遍历过程如下:
- 访问根节点 A。
- 递归遍历左子树,访问节点 B(左子树的根节点)。
- 递归遍历左子树,访问节点 D。
- 访问节点 D 后,没有左子树,返回到节点 B。
- 继续遍历节点 B 的右子树,访问节点 E。
- 节点 E 没有左子树和右子树,返回到节点 B。
- 返回到根节点 A,开始遍历右子树,访问节点 C。
- 节点 C 的左子树为空,继续遍历右子树,访问节点 F。
- 节点 F 没有左子树和右子树,返回到节点 C。
- 遍历完整个二叉树,遍历结束。
LDR:中序遍历
得到的表达式为中缀表示
例:

具体的遍历过程如下:
- 递归遍历左子树,访问节点 D。
- 访问节点 D 后,没有左子树,返回到节点 B。
- 继续遍历节点 B 的右子树,访问节点 E。
- 节点 E 没有左子树和右子树,返回到节点 B。
- 返回到根节点 A,访问节点 A。
- 递归遍历右子树,访问节点 C。
- 节点 C 的左子树为空,继续遍历右子树,访问节点 F。
- 节点 F 没有左子树和右子树,返回到节点 C。
- 遍历完整个二叉树,遍历结束。
LRD:后序遍历
得到的表达式为后缀表示
例:

具体的遍历过程如下:
- 递归遍历左子树,访问节点 D。
- 访问节点 D 后,没有右子树,返回到节点 B。
- 继续遍历节点 B 的右子树,访问节点 E。
- 节点 E 没有左子树和右子树,返回到节点 B。
- 返回到根节点 A,开始遍历右子树,访问节点 C。
- 节点 C 的左子树为空,继续遍历右子树,访问节点 F。
- 节点 F 没有左子树和右子树,返回到节点 C。
- 遍历完整个二叉树,返回到根节点 A,访问节点 A。
由遍历序列求二叉树:
由二叉树的先序序列和中序序列,或由二叉树的后序序列和中序序列可以确定唯一一颗二叉树
例:
先序:A B C D E F G H I J
中序:C D B F E A I H G J
由先序遍历可得,A为根节点,再结合中序序列,C D B F E在左子树上,I H G J在右子树上
由先序序列得B为左子树的根节点,再结合中序序列得C D在B的左子树上,F E在B的右子树上
由先序序列可得G为右子树的根节点,结合中序序列,I H在G左子树上,J在G的右子树上
由先序序列可得C为D的根节点,再结合中序序列,可得D在C的右子树上
同理可得E为根,F在E的左子树上;H为根,I在H左子树上
例:
中序:B D C E A F H G
后序:? D E C B H G F A
由后序遍历可得,A为根节点,结合中序遍历得BDCE在左子树上,FHG在右子树上
由后序遍历得,B为左子树的根节点,结合中序遍历的DCE在B的右子树上
由后序遍历得,C为根,再由中序遍历可得,D为C的左子树,E为C的右子树
由后序遍历得,F为根节点,有中序遍历得,HG在F右子树上
由后序遍历得,G为根,再由中序得,H在G得左子树上
遍历算法实现(链式存储结构):
先序遍历:
若二叉树为空,则空操作
若二叉树不为空,则先访问根节点,再先序遍历左子树,再先序遍历右子树
代码如下:

中序遍历:
?
后序遍历:

?
?遍历算法应用:
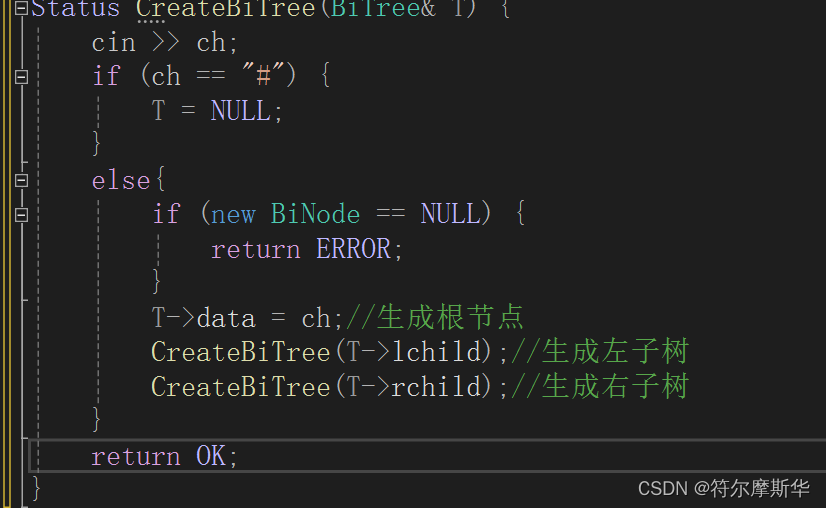
建立二叉树:
例:按顺序读入以下字符ABC##DE#G##F###(#指空结点)
代码如下:
?复制二叉树:

?计算二叉树深度:
如果是空树,则深度为0
否则,记左子树深度为m,右子树深度为n,比较后返回较大者加1

计算二叉树结点总数:
如果是空树,则节点个数为0
否则,节点个数为左子树的节点个数+右子树节点个数+1

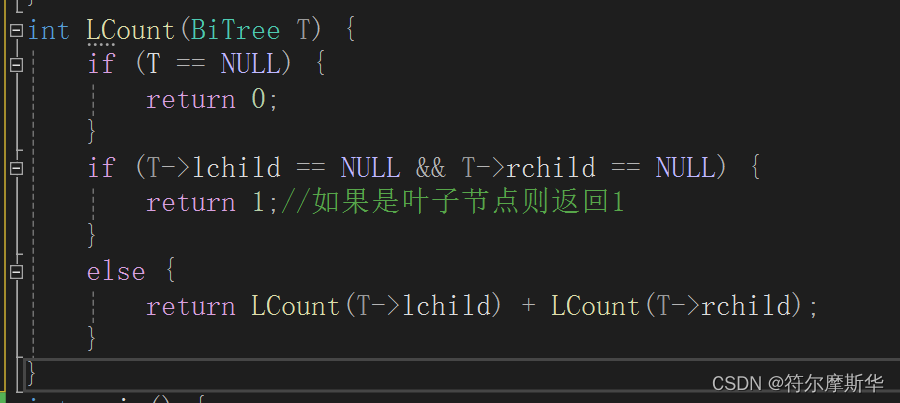
计算二叉树叶子结点数:
如果是空树,则叶子节点个数为0
否则,返回左子树的叶子节点个数+右子树的叶子结点个数
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!