Multi-Drone based Single Object Tracking with Agent Sharing Network阅读笔记
Multi-Drone based Single Object Tracking with Agent Sharing Network阅读笔记
Abstract
搭载摄像头的无人机可以从更广阔的视角在空中动态跟踪目标,与静态摄像头或地面移动传感器相比具有优势。然而,由于外观变化和严重遮挡等多种因素,使用单架无人机准确跟踪目标仍然是一个挑战。在本文中,我们收集了一个==新的多无人机单目标跟踪(MDOT)数据集,该数据集包含92组由两架无人机拍摄的113,918帧高分辨率视频片段,以及63组由三架无人机拍摄的145,875帧高分辨率视频片段。此外,特别为多无人机单目标跟踪设计了两种评估指标,即自动融合得分(AFS)和理想融合得分(IFS)==。更进一步,我们提出了一种代理共享网络(ASNet),通过自我监督的模板共享和对多架无人机目标的视觉感知融合,显著提高了跟踪精度,与单无人机跟踪相比有显著改进。在MDOT上的大量实验表明,我们的ASNet显著优于最近的最先进跟踪器。
Introduction
- 应用背景
- 无人机或通用无人机(UAV)在我们的日常生活中被广泛使用。具体而言,基于无人机的视觉跟踪应用场景包括现场直播、军事战场、犯罪调查、体育和娱乐等领域。与静态相机和手持移动设备相比,无人机可以动态移动并覆盖广阔的地面区域,非常适合跟踪快速移动的目标。
- 为了在无人机上执行稳健的跟踪,具有高质量注释的大规模数据集对于推动算法的发展起着至关重要的作用。最近,已经收集了一些单无人机的基准数据集,包括UAV123、Campus【4】、VisDrone-2018【2】和UAVDT【3】。如图1所示,与只在某个区域收集数据的静态相机相比,无人机还可以从更广的视角在空中动态跟踪目标。然而,这也给视觉跟踪带来了额外的挑战,包括目标微小、相机运动、目标高密度分布等。
- 为了解决上述问题,结合多架无人机是提高目标跟踪在遮挡和外观歧义方面的性能和稳健性的有效解决方案。因此,一些算法专注于基于多摄像头视频监控的长期跟踪和重新识别【5】【6】【7】【8】【9】【10】【11】【12】【13】。在过去的几年中,已经构建了一些具有相互重叠或非重叠视角的多摄像头基准数据集【14】【15】【11】。一些具有完全重叠视角的数据集受限于短时间间隔和受控条件【14】。这些多摄像头数据集专门为跨摄像头的多目标跟踪或人员重新识别收集。
尽管提供了许多用于视觉跟踪的数据集,但它们要么是为单无人机跟踪,要么是为多摄像头跟踪构建的。然而,很少有基准数据集用于多无人机视觉跟踪。在本文中,为了结合基于无人机的跟踪和多摄像头跟踪的优势,我们提出了一个多无人机单目标跟踪(MDOT)数据集。MDOT由92组由两架无人机拍摄的113,918帧高分辨率视频剪辑和63组由三架无人机拍摄的145,875帧高分辨率视频剪辑组成。在每组视频剪辑中,多架无人机跟踪同一个目标。此外,我们还标注了10种不同类型的属性,包括白天、夜晚、相机运动、部分遮挡、完全遮挡、视野外、类似物体、视角变化、光照变化和低分辨率。
为了评估我们数据集中的跟踪算法,我们**提出了两种新的评估指标,即自适应融合得分(AFS)和理想融合得分(IFS)。**具体来说:
- AFS衡量了使用在线融合策略融合跟踪结果的多无人机跟踪器的性能,
- IFS是当我们假设多无人机系统可以准确选择性能更好的无人机的跟踪结果时的理想融合性能。
另一方面,为了利用多无人机的互补性,我们提出了一个代理共享网络(ASNet),该网络以自我监督的方式跨无人机共享模板,并自动融合跟踪结果,以实现稳健和精确的视觉跟踪。我们还提出了一种基于无人机的跟踪器的重新检测策略,以解决目标漂移问题,当目标被判断为满足定义条件时,通过扩大搜索区域的大小。在MDOT上的实验表明,ASNet大大优于20种最新的最先进跟踪算法。
Multi-Drone single object tracking dataset
A. 数据收集
数据集是由多架DJI PHANTOM 4 Pro无人机收集的。具体来说,这些无人机由几名专业的人类操作员在不同高度和各种户外场景(例如,公园、校园、广场和街道)控制,如图2所示。为了增加目标外观和尺度的多样性,同一目标由多架无人机从不同视角和不同高度跟踪,高度范围从20米到100米。该数据集有155组视频剪辑,包含259,793帧高分辨率帧,分为两个子数据集。基于两架无人机的数据集(Two-MDOT)包括92组视频剪辑,由两架无人机拍摄的113,918帧高分辨率帧,而基于三架无人机的数据集(Three-MDOT)包含63组视频剪辑,由三架无人机拍摄的145,875帧高分辨率帧。Two-MDOT是在2018年收集的,而Three-MDOT是在2019年收集的。因此,Two-MDOT和Three-MDOT之间没有重叠。此外,该数据集被划分为训练集(Two-MDOT中的37组和Three-MDOT中的28组)和测试集(Two-MDOT中的55组和Three-MDOT中的35组)。
如表I所示,大多数以前的数据集都是由一台相机收集的,其中目标的外观并不丰富。尽管NLPR MCT和DukeMTMC用于评估多目标跟踪和人员重新识别,但它们是由静态相机收集的。相比之下,MDOT可以动态地用移动无人机跟踪目标(见图3)。需要注意的是,我们没有收集激光雷达数据,因为配备激光雷达的几架无人机与配备可见光相机的无人机相比要昂贵得多,而且激光雷达的准确感测距离大约为200米,与可见光相机相比没有明显优势。
B. 标注
对于标注,我们收集了1280×720尺寸的图像,并使用常用的标注工具VATIC来标注目标的位置、遮挡和视野外信息。之后,使用LabelMe逐帧细化和复核标注。此外,155个序列中的目标被划分为9个类别,即行人、汽车、马车、摩托车、自行车、三轮车、卡车、狗和公共汽车,每个类别中的目标也都是多样的。此外,如表II所示,所有序列均由10个属性标注,即白天(DAY)、夜晚(NIGHT)、相机运动(CM)、部分遮挡(POC)、完全遮挡(FOC)、视野外(OV)、类似物体(SO)、视点变化(VC)、光照变化(IV)和低分辨率(LR)。关于10个属性的统计数据在图4中总结。值得注意的是,CM、IV和LR在大多数序列中出现,这可能会显著降低跟踪器的性能。与经典单目标跟踪任务的设置类似,我们在不同无人机的第一帧手动标注了相同对象的跟踪目标。
C. 评价指标
单目标跟踪通常通过成功率和精确度图来评估。然而,对于基于多无人机的跟踪,算法的结果应当基于多无人机融合结果来评估。为此,我们提出了两个新的评价指标,用于多无人机单目标跟踪,即自动融合得分(AFS)和理想融合得分(IFS)。
-
自动融合得分(AFS) 评估使用在线融合策略融合跟踪结果的多无人机跟踪器的性能。
定义 1:设
h_i^v和y_i^v分别是第i帧和第v架无人机的跟踪结果(即,框的位置、宽度和高度)和真值。AFS定义为:
A F S = 1 n ∑ i = 1 n ∑ v = 1 V w v s ( h i v , y i v ) AFS = \frac{1}{n} \sum_{i=1}^{n} \sum_{v=1}^{V} w_v s(h_i^v, y_i^v) AFS=n1?∑i=1n?∑v=1V?wv?s(hiv?,yiv?)
其中 s(·,·) 是单目标跟踪的评价指标(即,成功率和精确度得分)而 w_v 是第 v 架无人机的权重。n 和 V 分别是视频剪辑中的帧数和无人机的数量。w_v 的值应该是零或一。w_v 是自动学习的,并且在跟踪过程中针对每一帧进行在线更新。
- 理想融合得分(IFS) 是当我们假设多无人机系统可以准确选择性能更好的无人机的跟踪结果时的理想融合性能。它被定义为评估多无人机跟踪系统的极端性能,可以指导设计更优秀的多无人机跟踪器。
定义 2:设 h_i^v 和 y_i^v 分别是第 i 帧和第 v 架无人机的跟踪结果和真值。IFS定义为:
I F S = 1 n ∑ i = 1 n max ? ( s ( h i 1 , y i 1 ) , … , s ( h i V , y i V ) ) IFS = \frac{1}{n} \sum_{i=1}^{n} \max(s(h_i^1, y_i^1), \ldots , s(h_i^V, y_i^V)) IFS=n1?∑i=1n?max(s(hi1?,yi1?),…,s(hiV?,yiV?))
在评估阶段,OPE(单次通过评估)指标是单目标跟踪器的传统指标。基于OPE,我们提出了AFS和IFS作为多无人机跟踪器的评估指标。与AFS相比,IFS展示了与多无人机融合的上界之间的差距,这启发我们设计具有更有用融合策略的优秀多无人机跟踪器。

Agent Sharing NetWork
IV. 代理共享网络
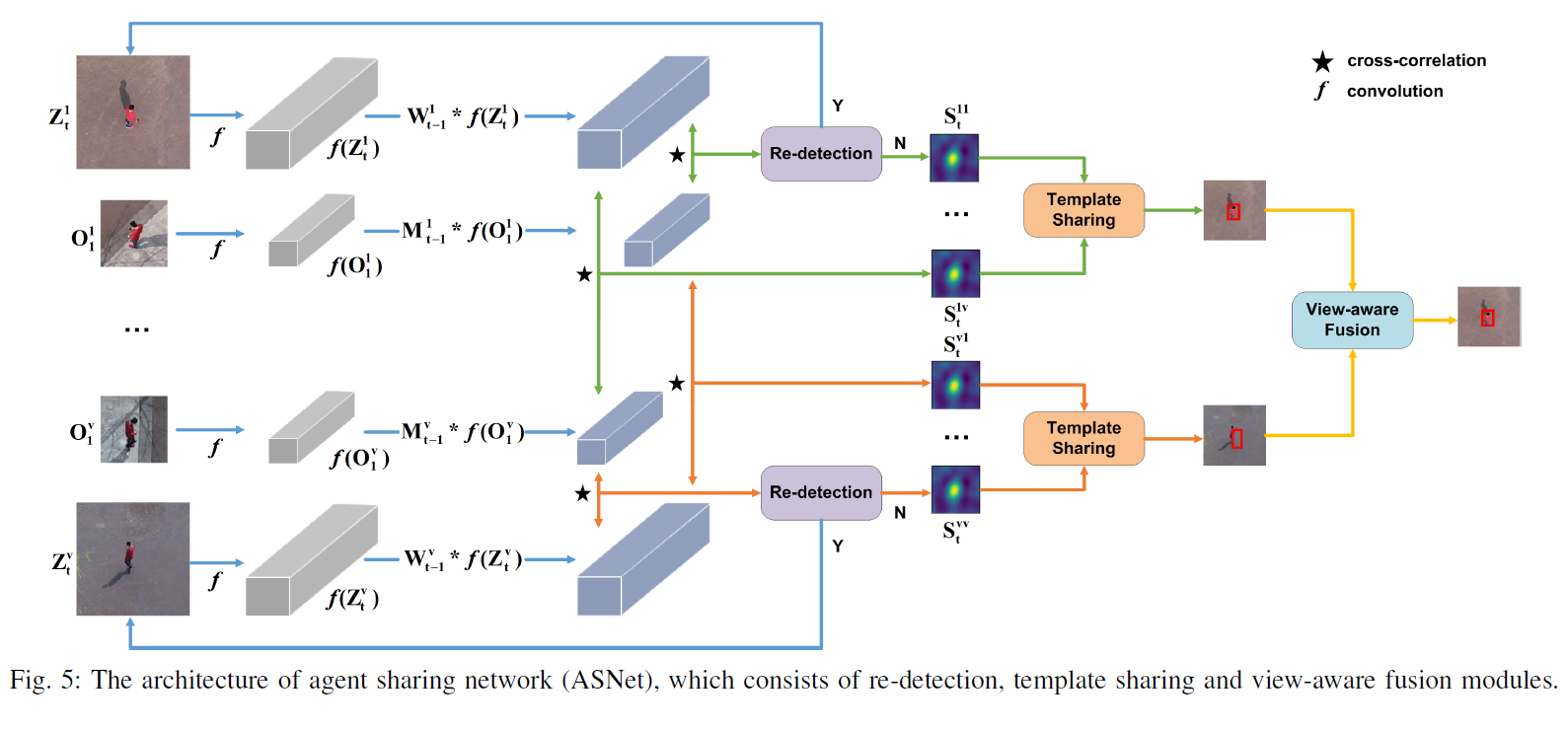
多无人机跟踪的关键挑战是如何共享无人机之间的信息并自适应融合跟踪结果。为了应对这一挑战,每架无人机被视为一个代理,我们提出了一个代理共享网络(ASNet)来有效利用无人机之间的互补信息,参见图5。
A. 网络架构
动态孪生网络(DSiam)【45】能够有效地进行目标外观变化和从前一帧中抑制背景的在线学习。因此,我们选择DSiam作为基础跟踪器,并开发相应的多无人机跟踪器。一个公共跟踪器被训练用于所有无人机跟踪同一个目标在同一场景中。因此,它不偏向任何不同的无人机。我们专注于在线跟踪过程,并从三个方面设计代理共享网络,即模板共享,视觉感知融合和目标重新检测。
设 O v 1 O_v^1 Ov1? 和 Z v t Z_v^t Zvt? 分别表示第一帧和第 t t t 帧对应于第 v v v 架无人机的模板和搜索区域。通过一个嵌入模块 f f f,例如,卷积神经网络(CNN),可以为模板和搜索区域提取深度特征,即 f ( O v 1 ) f(O_v^1) f(Ov1?) 和 f ( Z v t ) f(Z_v^t) f(Zvt?)。DSiam的关键组成部分是目标外观变化变换和背景抑制变换【45】。对于ASNet,我们需要为所有无人机确定变换。目标外观变化变换 M t ? 1 v M_{t-1}^v Mt?1v? 相对于第 v v v 架无人机是通过下面的方式学习的:
M t ? 1 v = arg ? min ? ∥ M ? F 1 v ? F t ? 1 v ∥ 2 + λ m ∥ M ∥ 2 , M_{t-1}^v = \arg \min \| M \otimes F_1^v - F_{t-1}^v \|^2 + \lambda_m \| M \|^2, Mt?1v?=argmin∥M?F1v??Ft?1v?∥2+λm?∥M∥2,
其中 F v 1 = f ( O v 1 ) F_v^1 = f(O_v^1) Fv1?=f(Ov1?) 和 F v t ? 1 = f ( O v t ? 1 ) F_v^{t-1} = f(O_v^{t-1}) Fvt?1?=f(Ovt?1?)。 O v t ? 1 O_v^{t-1} Ovt?1? 是第 t ? 1 t-1 t?1 帧的目标对于第 v v v 架无人机。 ? \otimes ? 表示circular convolution,可以在频率域中快速计算【45】。 M t ? 1 v M_{t-1}^v Mt?1v? 可以捕捉目标变化,在时间平滑假设下,因此大大贡献于在线学习。同样地,背景抑制变换 W t ? 1 v W_{t-1}^v Wt?1v? 也可以被学习:
KaTeX parse error: Can't use function '$' in math mode at position 56: …_{t-1}}^v - F_{$?\tilde{G}_{t-1}…
其中 G t ? 1 v G_{t-1}^v Gt?1v? 是以目标为中心且与 Z t ? 1 v Z_{t-1}^v Zt?1v? 大小相同的区域。 G ~ t ? 1 v \tilde{G}_{t-1}^v G~t?1v? 通过将 G t ? 1 v G_{t-1}^v Gt?1v? 与高斯权重图相乘得到。 W t ? 1 v W_{t-1}^v Wt?1v? 能够抑制背景信息,因此诱导出更好的跟踪性能。关于 M t ? 1 v M_{t-1}^v Mt?1v? 和 W t ? 1 v W_{t-1}^v Wt?1v? 的更多细节可以在【45】中找到。
与使用单架无人机的视觉跟踪相比,ASNet共享所有无人机的模板,并获取对应于多架无人机模板的响应图。由于多架无人机的模板可靠性不同,我们以自我监督的方式自适应融合多模板的响应图。最终,多架无人机的跟踪结果可以通过跟踪得分自适应融合。
这两个公式似乎是视觉跟踪领域中用于描述目标外观变化和背景抑制模型的优化问题。让我来帮您解释这两个公式的意思。
第一个公式定义了目标外观变化模型 ( M_{t-1}^v ) 的优化问题:
M t ? 1 v = arg ? min ? ∥ M ? F 1 v ? F t ? 1 v ∥ 2 + λ m ∥ M ∥ 2 , M_{t-1}^v = \arg \min \| M \otimes F_1^v - F_{t-1}^v \|^2 + \lambda_m \| M \|^2, Mt?1v?=argmin∥M?F1v??Ft?1v?∥2+λm?∥M∥2,
在这个公式中:
- ( M ) 是一个变换矩阵,用于表示目标外观从第一帧到第 ( t-1 ) 帧的变化。
- ( F_1^v ) 是在第一帧中,第 ( v ) 架无人机视角下目标的特征。
- ( F_{t-1}^v ) 是在第 ( t-1 ) 帧中,相同无人机视角下目标的特征。
- ( \otimes ) 表示卷积操作。
- ( \lambda_m ) 是正则化参数,用于平衡目标外观变化模型的复杂性和拟合程度。
这个优化问题的目的是找到一个模型 ( M ),使得通过该模型变换后的第一帧目标特征与第 ( t-1 ) 帧目标特征之间的差异最小,同时保持模型 ( M ) 的复杂性尽可能低。
第二个公式定义了背景抑制模型 ( W_{t-1}^v ) 的优化问题:
W t ? 1 v = arg ? min ? ∥ W ? F G t ? 1 v ? F G ~ t ? 1 v ∥ 2 + λ w ∥ W ∥ 2 , W_{t-1}^v = \arg \min \| W \otimes F_{G_{t-1}}^v - F_{\tilde{G}_{t-1}}^v \|^2 + \lambda_w \| W \|^2, Wt?1v?=argmin∥W?FGt?1?v??FG~t?1?v?∥2+λw?∥W∥2,
在这个公式中:
- ( W ) 是一个变换矩阵,用于表示背景的抑制。
- ( F_{G_{t-1}}^v ) 和 ( F_{\tilde{G}_{t-1}}^v ) 表示第 ( v ) 架无人机在第 ( t-1 ) 帧的背景特征。
- 同样,( \otimes ) 表示卷积操作。
- ( \lambda_w ) 是正则化参数,用于平衡背景抑制模型的复杂性和拟合程度。
这个优化问题的目的是找到一个模型 ( W ),使得通过该模型变换后的背景特征与真实背景特征之间的差异最小,同时保持模型 ( W ) 的复杂性尽可能低。
在这两个公式中,“( \arg \min )”表示我们的目标是最小化后面的表达式,并找到使这个表达式最小化的变换矩阵 ( M ) 或 ( W )。
\lambda_m是正则化参数,用于平衡目标外观变化模型的复杂性和拟合程度。 为什么lambda_m可以平衡目标外观变化模型的复杂性和拟合程度?
在优化问题中,正则化参数(如
\(\lambda_m\))用来平衡模型的复杂性(通常关联于模型的过拟合风险)和模型对数据的拟合程度。这是通过在损失函数中加入一个额外的项来实现的,该项通常与模型参数的规范(或大小)有关。具体来说:
模型复杂性:如果模型过于复杂,它可能会过度拟合训练数据,即它可能会记住训练数据的噪声而不是其潜在的结构。在上述情况中,( M ) 的复杂性可以通过 ( M ) 的规范(例如,( | M |_2^2 ))来衡量,这是 ( M ) 所有元素的平方和。
拟合程度:模型对数据的拟合程度可以通过模型的预测(在这种情况下是 ( M \otimes F_1^v ))和真实数据 ( F_{t-1}^v ) 之间的差异来衡量,通常使用二范数(即 ( | \cdot |_2^2 ))。
正则化参数 ( \lambda_m ) 控制了正则化项 ( | M |2^2 ) 相对于拟合误差项 ( | M \otimes F_1^v - F{t-1}^v |_2^2 ) 的重要性。当 ( \lambda_m ) 较大时,优化过程会更多地惩罚模型复杂性,从而倾向于选择一个更简单的 ( M ) 来避免过拟合。相反,当 ( \lambda_m ) 较小时,优化过程会更多地关注减少拟合误差,可能会导致一个更复杂的 ( M ),这可能会提高模型在训练数据上的性能,但可能降低其泛化能力。
因此,( \lambda_m ) 的选择决定了模型的复杂性与拟合数据能力之间的权衡,这是机器学习中调整模型性能的关键实践。
B. 自我监督模板共享
由于目标的外观可能会有很大的变化,所有无人机的模板可以共享以提高单个无人机跟踪器的鲁棒性。第 k k k 架无人机的响应图 S t k v S_{t}^{kv} Stkv?,对应于第 v v v 架无人机的模板,计算如下:
S t k v = corr ( M t ? 1 v ? f ( O 1 v ) , W t ? 1 ? f ( Z t k ) ) , S_{t}^{kv} = \text{corr}(M_{t-1}^{v} \otimes f(O_{1}^{v}), W_{t-1} \otimes f(Z_{t}^{k})), Stkv?=corr(Mt?1v??f(O1v?),Wt?1??f(Ztk?)),
其中 corr ( A , B ) \text{corr}(A, B) corr(A,B) 是相关操作,可以被视为以 A A A 为卷积滤波器对 B B B 进行的卷积操作。对于第 k k k 架无人机,我们获得了一组响应图 S t k 1 , S t k 2 , . . . , S t k V S_{t}^{k1}, S_{t}^{k2}, ..., S_{t}^{kV} Stk1?,Stk2?,...,StkV?。为了融合响应图,我们提出了一种自我监督的融合策略。具体来说,我们使用前 t ? 1 t-1 t?1 帧的跟踪结果作为监督信息来指导 V V V 个模板的权重学习。设 O t k v O_{t}^{kv} Otkv? 表示第 k k k 架无人机上跟踪器跟踪的目标,使用第 v v v 架无人机的模板。融合权重 u t k u_{t}^{k} utk? 可以通过以下方式学习得到:
min ? u ∥ D t k u t k ? M t ? 1 k ? f ( O 1 k ) ∥ 2 + λ u ∥ u t k ∥ 2 , \min_{u} \left\| D_{t}^{k} u_{t}^{k} - M_{t-1}^{k} \otimes f(O_{1}^{k}) \right\|^{2} + \lambda_{u} \left\| u_{t}^{k} \right\|^{2}, umin? ?Dtk?utk??Mt?1k??f(O1k?) ?2+λu? ?utk? ?2,
其中 D t k = [ f ( O t k 1 ) , f ( O t k 2 ) , . . . , f ( O t k V ) ] D_{t}^{k} = [f(O_{t}^{k1}), f(O_{t}^{k2}), ..., f(O_{t}^{kV})] Dtk?=[f(Otk1?),f(Otk2?),...,f(OtkV?)]。权重反映了跟踪目标和目标模板在 ( t ? 1 ) (t-1) (t?1) 帧之间的相关性。考虑到学习到的权重和响应图,我们可以获得第 k k k 架无人机上跟踪器的融合响应图,即:
S t k = ∑ v = 1 n u t k v S t k v . S_{t}^{k} = \sum_{v=1}^{n} u_{t}^{kv} S_{t}^{kv}. Stk?=v=1∑n?utkv?Stkv?.
对于一个有 V V V 架无人机的多无人机跟踪系统,我们总共可以获得 V V V 个融合响应图,即 S t 1 , S t 2 , . . . , S t V S_{t}^{1}, S_{t}^{2}, ..., S_{t}^{V} St1?,St2?,...,StV?。
C. 视角感知融合
为了在多无人机跟踪上生成最终结果,我们在获得 V V V 个融合响应图后使用自动视角感知融合方案。对于第 k k k 架无人机的响应图,我们在响应图中搜索最大值 g ( S t k ) g(S_{t}^{k}) g(Stk?),并获取其对应位置 p t k : g ( S t k ) p_{t}^{k} : g(S_{t}^{k}) ptk?:g(Stk?) 被定义为第 t t t 帧在第 k k k 架跟踪器上的跟踪分数。然后,我们可以通过以下方式获得最佳响应图的索引 b t b_{t} bt?:
b t = arg ? max ? ( g ( S t 1 ) , g ( S t 2 ) , . . . , g ( S t V ) ) . b_{t} = \arg \max(g(S_{t}^{1}), g(S_{t}^{2}), ..., g(S_{t}^{V})). bt?=argmax(g(St1?),g(St2?),...,g(StV?)).
在第 b t b_{t} bt? 架无人机上的目标位置 p t b t p_{t}^{b_{t}} ptbt?? 是最佳响应图的位置。从方程式 8 获得的最佳响应图的无人机跟踪器的权重 w v w_{v} wv? 被设置为 1,其余为 0。
D. 目标重新检测
由于在基于无人机的跟踪中经常发生相机移动,目标位置可能在连续帧中变化很大。为了解决这个问题,我们使用基于过去和当前帧的目标重新检测策略。对于第 t t t 帧,设 I t q I_{t}^{q} Itq? 表示过去 q q q 帧的一组分数。 μ t q \mu_{t}^{q} μtq? 和 σ t q \sigma_{t}^{q} σtq? 分别表示 I t q I_{t}^{q} Itq? 的均值和标准差。受 MOSSe 中峰值到旁瓣比的启发【46】,目标重新检测的阈值定义为:
ω t q = μ t q ? λ ? σ t q , \omega_{t}^{q} = \mu_{t}^{q} - \lambda \cdot \sigma_{t}^{q}, ωtq?=μtq??λ?σtq?,
其中 λ \lambda λ 是一个预设参数。当分数小于 ω t q \omega_{t}^{q} ωtq? 或跟踪分数是阈值 T s c o r e T_{score} Tscore? 时,目标可能丢失。如果是这样,我们使用局部到全局策略逐步扩展搜索区域以重新检测目标【21】。在使用了所提出的重新检测策略后,跟踪性能大幅提升。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!