12.5,12.15AVL树更新,定义,插入
?定义平衡因子为右子树高度减去左子树高度
AVL树插入分为两步:
- 按照二叉搜索树的方式插入新节点
- 调整平衡因子
对于平衡因子的调整,在插入之前,所有节点的平衡因子分为三种情况:0,1,-1插入后,新插入节点可能会使它的父节点的平衡因子发生变化,有这么三种情况:
1.新插入节点的父节点(parent)的平衡因子变成0(一定是由1或-1变成0)
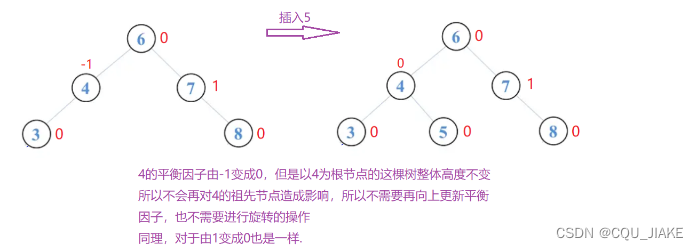
2.新插入节点的父节点(parent)的平衡因子变成-1/1(由0变成1或-1)
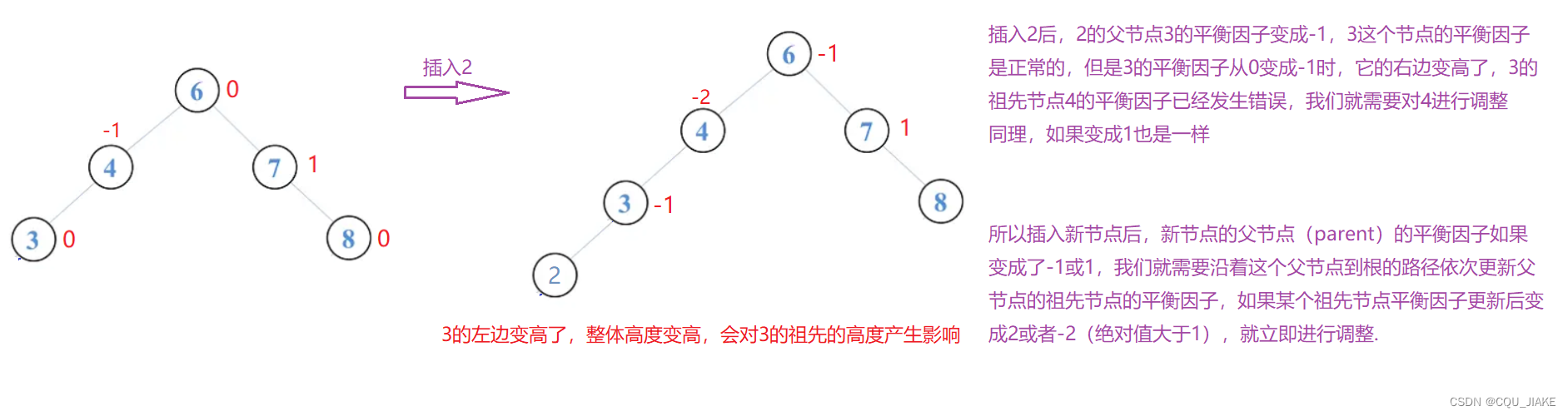
3.新插入节点的父节点的平衡因子变成2/-2,此时已经违反了平衡树的性质,需要对其进行旋转处理.
AVL操作
更新
BST旋转
结点旋转操作对不同的BST树操作方式都是一样的

1.Insert 1, 2, 3, 4, 5, and 6 one by one into an initially empty AVL tree. Then the preorder traversal sequence of the resulting tree must be {4, 2, 1, 3, 5, 6}.?
什么时候需要旋转??怎么旋转??



弄懂文章
PTA选择题复习,
编程题
那个题弄懂(如果可以再练习一道)?
复习几个文章
AVL
AVL树定义
template<class K, class V>
struct AVLNode
{
AVLNode<K, V>* _left;
AVLNode<K, V>* _right;
AVLNode<K, V>* _parent;
std::pair<K, V> _kv;
int _bf;
?
AVLNode(const std::pair<K, V>& kv = std::pair<K, V>())
: _left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _bf(0)
{ }
};即相比普通BST,多一个量为bf,表示平衡因子
此处默认BF=左子树高度减去右子树高度
平衡因子为0,说明没有孩子结点或者左右子树高度相同
平衡因子为1,说明没有右孩子结点或者左子树比右子树高度高1
平衡因子为-1,说明没有左孩子结点或者右子树比左子树高度高1
插入(两种底层情况)
当新增的节点 *cur(指向节点的指针为 cur) 插入到其双亲节点 *parent(指向节点的指针为 parent)的左边时,双亲节点的平衡因子 +1;反之,当新增的节点插入到其双亲节点的右边时,双亲节点的平衡因子 -1。
- 若双亲节点的平衡因子原来为 -1 或者 1,在它的左边或者右边插入新增的节点后,它的平衡因子变为 0。由于以 *parent 为根节点的子树的高度没有发生变化,因此也不会影响除 *parent 以外的其它祖先节点的平衡因子,插入完成。?
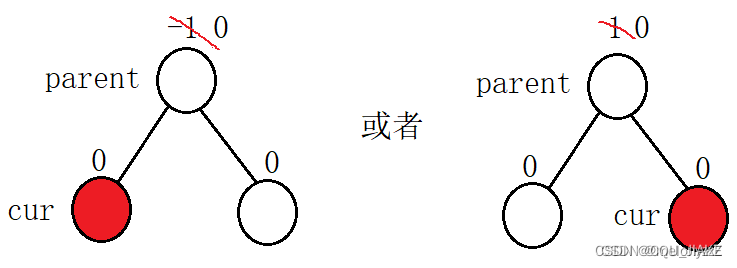
这种情况,仅考虑最底层的叶子节点与非叶子结点,即原来为-1,1,就说明最底层的非叶子结点只有一个孩子,然后现在插入,就是插入到另一个没孩子的位置上去。
由于之前有孩子,而且新插入的位置不在原来有孩子的基础上(如果是在原来有孩子的基础上,实际上是可以看成第2种情况)
? - 若双亲节点的平衡因子原来为 0,在它的左边或者右边插入新增的节点后,它的平衡因子变为 1 或者 -1。由于以 *parent 为根节点的子树的高度增高了 1,此时也就会影响其它祖先节点的平衡因子,需要往上更新。
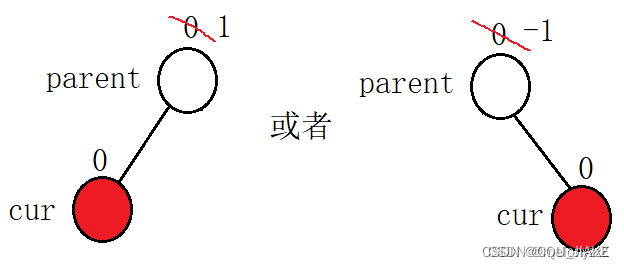
这种情况就是说之前没孩子,然后现在插入,使其多一个孩子
由此,就是插入的两种情况,所有插入类型本质上都是这两种情况,对于AVL树,其底层。
即插入的结点,是有孩子还是没孩子,其只关注插入层与上一层(parent层),即类似与在左孩子的位置上继续向左插入的情况,就是视为以左孩子为父母层的插入情况,即第二种
BF、高度变化特点
所以也就是对于BF,第一种情况时,只改变插入的父母结点的平衡因子,不影响祖辈结点的平衡因子(因为其子树高度没发生变化),特点为父母结点初始为1或-1,插入完后为0;第二种情况时,改变父母与祖辈的平衡因子,特点为父母结点初始为0,插入完后增减1,同时,往上更新祖辈结点平衡因子
具体来说,如果插入新节点的路径是左子树,那么从插入节点往上遍历的祖先节点,其平衡因子都需要增加1。如果插入新节点的路径是右子树,那么祖先节点的平衡因子都需要减去1。
如果某个祖先节点的平衡因子更新为0,说明平衡已恢复,插入操作完成。
如果某个祖先节点的平衡因子更新为1或-1,说明需要继续向上更新,直到达到根节点为止。当根节点的平衡因子也更新为0、1或-1时,表示整个插入操作完成。
然而,当某个祖先节点的平衡因子更新为2或-2时,(注意是某个祖先结点,不一定是根节点)表示出现了最小不平衡子树。此时,需要进行平衡调整来恢复AVL树的平衡。平衡调整的方法通常有LL旋转、RR旋转、LR旋转和RL旋转等。
总结起来,插入新节点后,除了更新新节点的双亲节点的平衡因子外,还需要继续往上更新祖先节点的平衡因子,并在出现最小不平衡子树时进行平衡调整以维持AVL树的平衡性
在AVL树的插入操作中,我们需要更新插入节点的祖先节点的平衡因子,以保持树的平衡性。当插入节点的平衡因子更新为1或-1时(原始为0),说明插入节点的子树高度发生了变化,这可能导致祖先节点的平衡因子也需要更新。
考虑以下情况:
1. 如果插入节点的路径在祖先节点的左子树上,即插入节点是祖先节点的左子节点。那么插入节点的插入会导致该祖先节点的平衡因子增加1。但是,由于插入节点的子树高度发生了变化,也可能影响到该祖先节点的平衡因子,使之变为1或-1。因此,我们需要继续向上更新祖先节点的平衡因子,以确保整棵树的平衡性。
2. 同样地,如果插入节点的路径在祖先节点的右子树上,即插入节点是祖先节点的右子节点。那么插入节点的插入会导致该祖先节点的平衡因子减少1。但是,插入节点的子树高度的变化也可能对该祖先节点的平衡因子产生影响,使之变为1或-1。因此,我们同样需要向上更新祖先节点的平衡因子来维持树的平衡。
两种插入的底层逻辑就是,第一种为原来根节点的平衡因子不为0,即左右子树一高一低,或者一个有,一个没有的情况,然后插入使高度相同,即由1或-1变为0
第二种为原来平衡因子为0,即左右子树高度相同,或者都没有,然后插入使高度不同,变为一高一低
这样,第一种插入后,根节点高度不变,只是高度相同了;第二种高度会变化,插入沿途路径高度增加1
往上更新(三种可能情况)
往上更新其它祖先节点的平衡因子的方式和一开始插入新增节点 *cur 时更新其双亲节点 *parent 的平衡因子的方式是一样的,即如果 *cur 在祖先节点的左子树中,则祖先节点的平衡因子 +1;如果 *cur 在祖先节点的右子树中,则祖先节点的平衡因子 -1。
如果祖先节点的平衡因子被更新为 0,则说明更新完成了,也意味着插入完成了。
如果祖先节点的平衡因子被更新为 1 或者 -1,则说明还需要继续往上更新(说明原来是0,不然就不可能平衡为AVL,现在为1或-1,则意味着祖先的子树高度发生了变化),直到某个祖先节点的平衡因子被更新为 0,或者直到更新完根节点,当根节点的平衡因子被更新为 0、1 或者 -1 时,意味着更新和插入也都完成了。
如果祖先节点的平衡因子被更新为 2 或者 -2(即其较高的子树增高了),就需要对以该节点为根节点的子树(称为最小不平衡子树)做平衡调整来恢复平衡。
对于祖先结点的树高发生变化,考虑,首先一定是第二种情况使其发生了变化,然后平衡因子变化,就是某一子树高度发生了变化,但祖先结点的高度不一定发生变化,即插入的位置在原来比较矮的子树里,这时候,实际上就会导致该祖先结点的BF变为0,且祖先结点高度不变;但如果原来是一样高,插入后就会变化为1或-1,进而使祖先结点高度发生变化,从而需要沿着祖先节点向上继续调整,找到祖先的祖先,因祖先结点是祖先的祖先结点的子树,其高度发生变化,祖先祖先结点高度也可能会发生变化。递归这一过程,直到根节点或某祖先结点BF变为0(意味该祖先结点高度不变,那么往上的BF也都不会再发生变化,实际相当于第一种插入情况)
而如果在变高调整过程中,出现BF为2,-2的情况,就需要进行相应的旋转调整
即向上调整会出现的三种底层情况

如果祖先结点BF更新为0,相当于第一种插入情况,即往缺孩子的那一块插入,使树更平衡,同时结点高度未发生变化,所以再往上也都不会发生变化
如果更新为1或-1,相当于第二种情况,即原来左右是等高的,因为插入,从而使结点的高度,BF(尤其是高度)发生了变化,所以才需要往上去进行调整,因为子树的高度变化了
第三种情况就是被视为底层的两种插入情况时的补全情况,注意是最小不平衡子树,最小的概念
平衡调整(四种情况)
首先需要注意如何进行平衡调整与插入无关,即需要平衡调整时,怎样进行调整不在插入时判断,而是在需要调整时判断
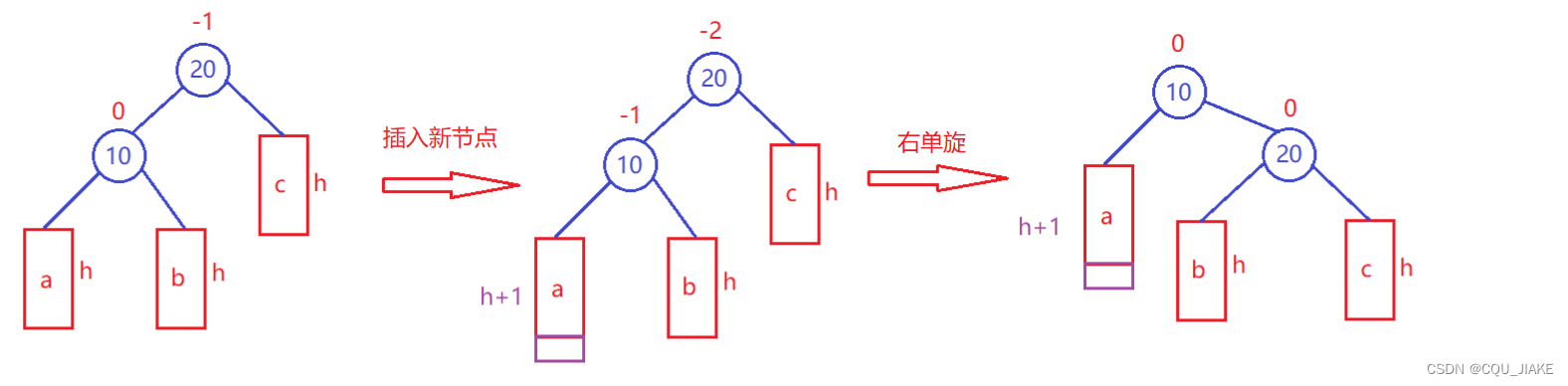
LL 型:由于在 A 左子树根节点的左子树上插入节点,A 的平衡因子由 1 增至 2,致使以 A 为根节点的子树失去平衡,则需进行一次向右的顺时针旋转操作。
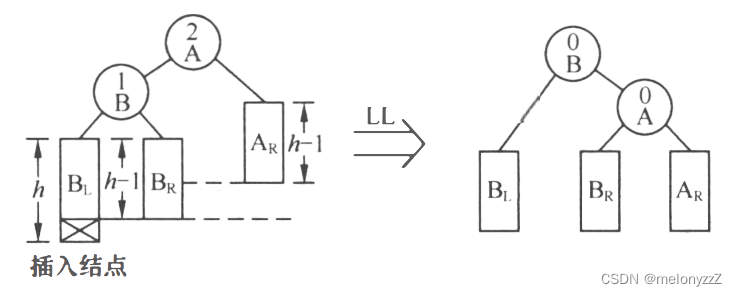
原根结点为A,新根节点为B,核心逻辑为
node* nroot = a->lchild;
a->lchild = nroot->rchild;
nroot->rchild = a;void LL(Node* pA)
{
Node* pB = pA->_left;
Node* pBR = pB->_right;
?
pA->_left = pBR;
if (pBR)
pBR->_parent = pA;
?
pB->_right = pA;
Node* tmp = pA->_parent;
pA->_parent = pB;
pB->_parent = tmp;
?
if (tmp == nullptr) // 或者 _root == pA
{
_root = pB;
}
else
{
if (tmp->_left == pA)
tmp->_left = pB;
else
tmp->_right = pB;
}
?
pA->_bf = pB->_bf = 0;
}RR 型:由于在 A 的右子树根节点的右子树上插入节点,A 的平衡因子由 -1 变成 -2,致使以 A 为根节点的子树失去平衡,则需进行一次向左的逆时针旋转操作。

void RR(Node* pA)
{
Node* pB = pA->_right;
Node* pBL = pB->_left;
?
pA->_right = pBL;
if (pBL)
pBL->_parent = pA;
?
pB->_left = pA;
Node* tmp = pA->_parent;
pA->_parent = pB;
pB->_parent = tmp;
?
if (tmp == nullptr) // 或者 _root == pA
{
_root = pB;
}
else
{
if (tmp->_left == pA)
tmp->_left = pB;
else
tmp->_right = pB;
}
?
pA->_bf = pB->_bf = 0;
}LR 型:由于在 A 的左子树的根节点的右子树上插入节点,A 的平衡因子由 1 增至 2,致使以 A 为根节点的子树失去平衡,则需要进行两次旋转操作。
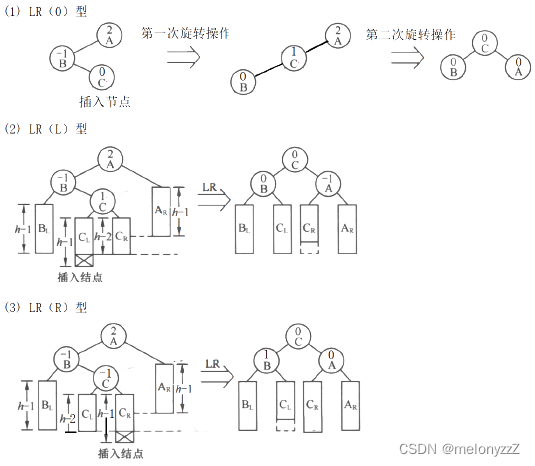
区分LR型的,就是结点C的平衡因子;但无论是那种LR型,操作都是一样的,就是先左旋,然后右旋
就是依据C的平衡因子,确定最后A,B,C的平衡因子?
void LR(Node* pA)
{
Node* pB = pA->_left;
Node* pC = pB->_right;
int bf = pC->_bf;
?
RR(pB);
LL(pA);
?
if (bf == 0) // LR(0)型
{
pA->_bf = 0;
pB->_bf = 0;
pC->_bf = 0;
}
else if (bf == 1) // LR(L)型
{
pA->_bf = -1;
pB->_bf = 0;
pC->_bf = 0;
}
else if (bf == -1) // LR(R)型
{
pA->_bf = 0;
pB->_bf = 1;
pC->_bf = 0;
}
}RL 型:由于在 A 的右子树根节点的左子树上插入节点,A 的平衡因子由 -1 变为 -2,致使以 A 为根节点的子树失去平衡,则旋转方法和 LR 型对称,也需进行两次旋转,先顺时针右旋,再逆时针左旋。

void RL(Node* pA)
{
Node* pB = pA->_right;
Node* pC = pB->_left;
int bf = pC->_bf;
?
LL(pB);
RR(pA);
?
if (bf == 0) // RL(0)型
{
pA->_bf = 0;
pB->_bf = 0;
pC->_bf = 0;
}
else if (bf == 1) // RL(L)型
{
pA->_bf = 0;
pB->_bf = -1;
pC->_bf = 0;
}
else if (bf == -1) // RL(R)型
{
pA->_bf = 1;
pB->_bf = 0;
pC->_bf = 0;
}
}总结:无论哪一种情况,在经过平衡旋转处理之后,以 B 或 C 为根的新子树为平衡二叉树,而且它们的高度和插入之前以 A 为根的子树相同。因此,当平衡的二叉搜索树因插入节点而失去平衡时,仅需对最小不平衡子树进行平衡旋转处理即可。
高度和A高度相同,就说明旋转不会使高度发生变化,只是调整BST,使之平衡,所以就不需要再向上继续调整了
此外,所谓0型RL,LR,就是建立在第二种插入的基础上,最简单的一种,即被插入的结点(B)就没有结点,为叶子结点,
L,R型的不平衡,也是建立在第二种插入的基础上,(第二种插入的底层逻辑是,根节点平衡因子为0,即左右子树高度相同或都没有,然后插入后,使这一情况发生了改变),被插入的结点(C)有孩子结点,只是高度相同,然后插入使之高度发生变化,进而导致C的高度发生变化,进而导致B的高度发生变化,进而导致A的高度发生变化,且A的平衡因子超过1或-1
即L,R型,就是对应着在插入前的,已经致密的,左右子树处处相等的介稳态,即插入前CL,CR高度相同,BL,BR(即C)高度相同
总结一下就是,不平衡就两种本质情况,即BF=2或BF=-2
然后依据BF=2,-2的具体情况再延申出4种具体情况
BF=2,-2说明插入前的BF为1或-1
BF=2说明左子树比右子树高2,即往左子树插了一个值,然后使左子树高度加了1(只有第二种插入方式才会使高度发生变化),左子树可能有左右结点,若其左右子树的高度相同或都没有时,插入(为第二种形式),使左子树高度增加,进而使根节点高度增加,BF变为2;若左右子树高度不同,当插到高的那个子树上时,那么此时的A就不再是最小不平衡子树,即考虑此时的情况就没有意义了,因为在底层时就会进行调整,表现到A的左子树时,左子树的左右子树高度就相等了;当左右子树高度不同,插到低的那个子树上时,相当于第一种插入,不会影响高度
删除
AVL 树的删除算法与二叉搜索树类似,不同之处在于:若删除后破坏了 AVL 树的高度平衡性质,还需要做平衡化旋转。
如果被删节点 *cur 的左、右子树都不为空。首先找到左子树中键值最大的节点 *leftMax(或者找到右子树中键值最小的节点 *rightMin),然后进行交换,即 std::swap(cur->_kv, leftMax->_kv);, 此时被删节点就变成了 *leftMax,该节点的右子树一定为空。
如果被删节点 *cur 最多只有一个孩子 *child。可以把 *cur 的双亲节点 *parent 中原来指向 *cur 的指针改为指向 *child。如果 *cur 没有孩子,则 *parent 的相应指针置为 nullptr。由于以 *parent 为根节点的子树的高度缩短了 1,所以需沿着 *parent 通向根节点的路径,往上追踪高度的这一变化对路径上各个节点的影响。
判断是否需要向上调整的关键条件,本质条件为,结点的高度是否发生变化,如果发生变化,那么向上去调整,不然就不继续向上调整
考查 *cur 的祖先节点,若 *cur 在祖先节点的左子树中,则祖先节点的平衡因子 -1,反之,则祖先节点的平衡因子 +1。根据祖先节点更新后的平衡因子,按以下三种情况分别进行处理:
- 祖先节点的平衡因子原来为 0,在它的左子树或者右子树被缩短后,它的平衡因子变为 -1 或者 1。由于以该节点为根的子树的高度没有改变,则不需要往上更新了,删除结束。
变为1就是说删除右子树中的结点,变为-1就是删除左子树中的结点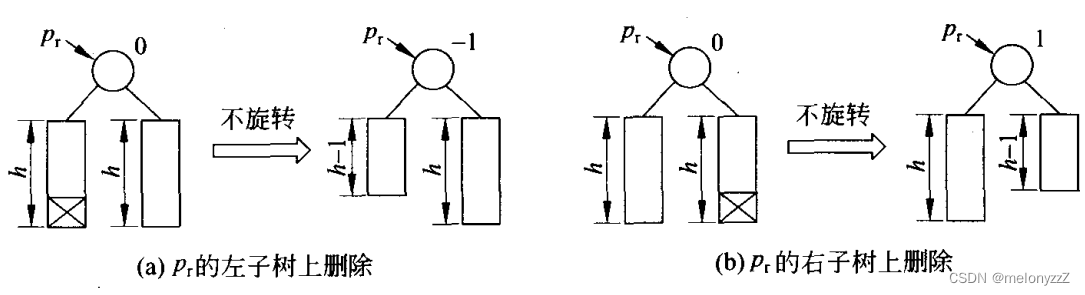
-
祖先节点的平衡因子原来为 1 或者 -1,在它的较高的子树被缩短后,它的平衡因子改为 0。此时以该节点为根的子树平衡,但其高度减 1,所以需要继续往上更新。
继续往上调整,就是防止情况为,在该根节点上的祖先节点中,该根节点为其中高度较小的子树,然后因为删除,使其高度变小,从而导致祖先节点可能不平衡,也就是第三种情况中的某些底层为这一情况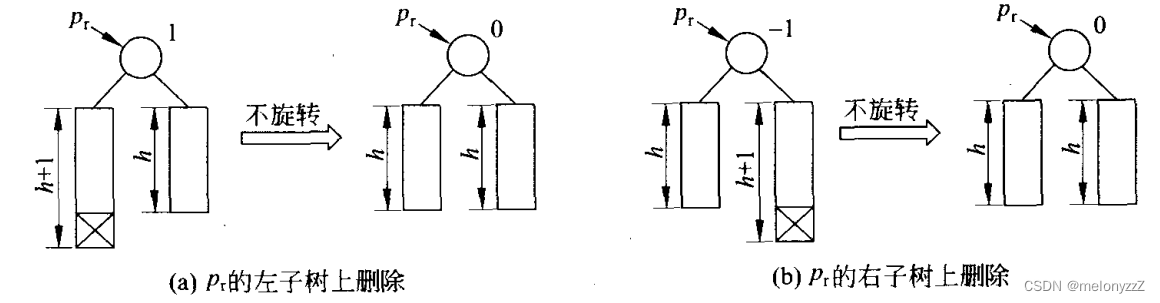
-
祖先节点的平衡因子原来为 -1 或者 1,在它的较矮的子树被缩短后,它的平衡因子变为 -2 或者 2。此时以该节点为根的子树不平衡,需要进行平衡化旋转来恢复平衡。
根据祖先节点较高的子树的根(该子树未被缩短)的平衡因子,有如下 3 种平衡化操作:
(1) 如果祖先节点较高的子树的根的平衡因子为 0,则执行一个单旋转来恢复子树的平衡。

由于旋转平衡后以 *q 为根节点的子树的高度没有发生改变,所以不需要再往上更新了,删除结束。
(2) 如果祖先节点较高的子树的根的平衡因子和祖先节点的平衡因子的正负号相同,则执行一个单旋转来恢复平衡。
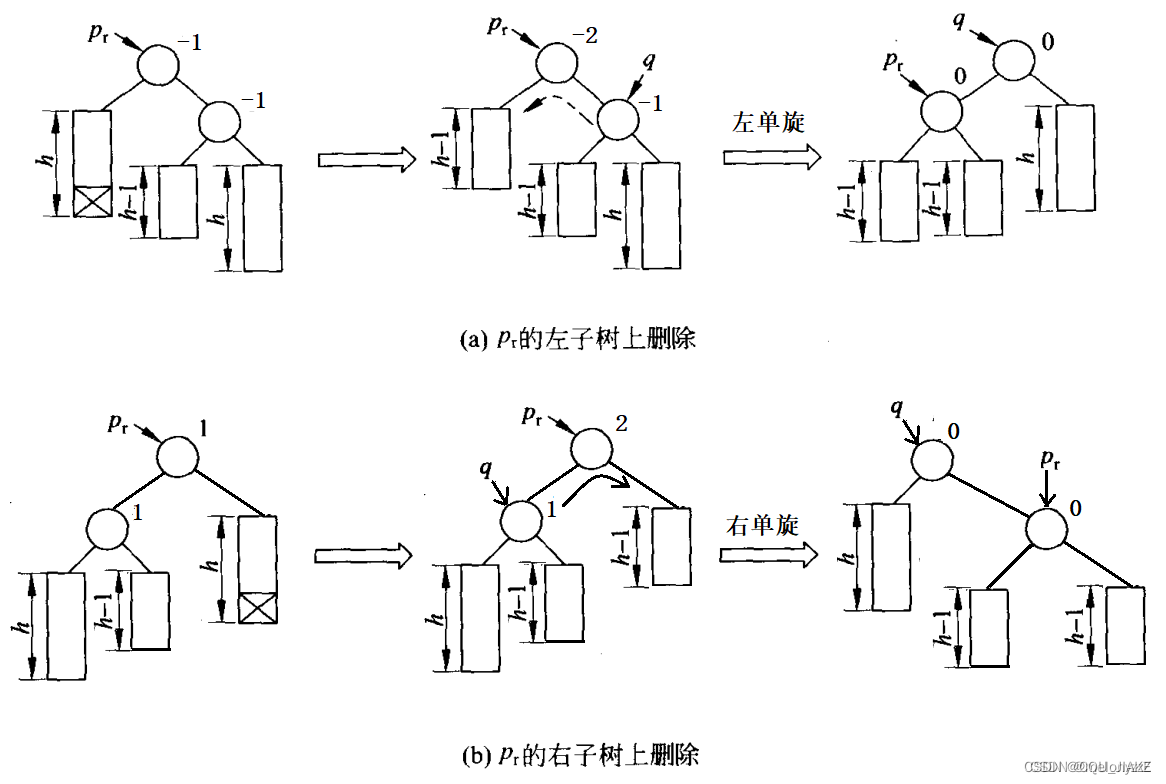
由于经过旋转平衡旋转后以 *q 为根节点的子树的高度降低了 1,所以需要继续往上更新。
(3) 如果祖先节点较高的子树的根的平衡因子和祖先节点的平衡因子的正负号相反,则执行一个双旋转来恢复平衡。

由于经过平衡化处理后以 *r 为根的子树的高度降低了 1,所以还需要继续往上更新。
?
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!