支持向量机（SVM）

在做二分类问题时，支持向量机（SVM）是一种非常强大且广泛应用的方法。我们在做二分类问题时，通常会生成如下图的分类方法：

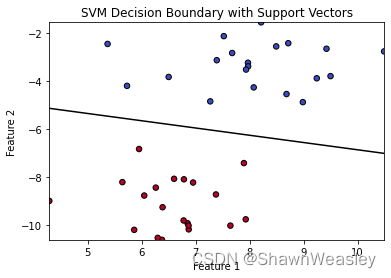
但从数据的角度来说，下面的分割方式似乎也没问题：

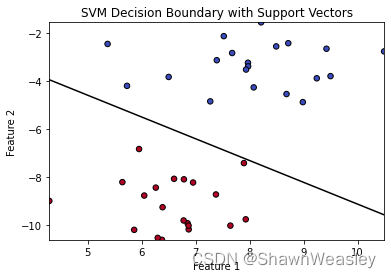
这时候支持向量机的作用就体现出来了，支持向量机致力于找到一条最优的决策边界，如下图：

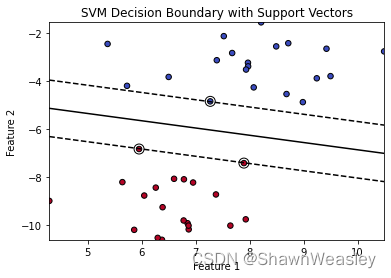
使用距离决策边界最近的三个点（在这里就称为支持向量），让这三个点到决策边界的距离相等。

优势

在SVM中，我们不仅要找到一个分隔两类数据的超平面，还希望建立一个尽可能宽的间隔，以提高模型对新样本的分类能力。这个最大化间隔的概念是SVM区别于其他分类器的关键特性。此外，数据特征可能远不止二维，SVM的真正威力在于它能够在任何维度的数据中找到这样的一个决策边界。

支持向量

支持向量是离决策边界最近的那些点。实际上，决策边界完全由这些点确定，而不是由所有的样本点确定。只有这些点对最终模型的建立是有影响的，这也是“支持向量机”这一名字的由来。

应用

SVM因其鲁棒性和有效性，在诸多领域都有应用，从图像识别、生物信息学到自然语言处理等。特别是在数据维度高，但样本数量相对较少的问题中，SVM表现尤为出色。

尽管最常见的SVM是用于二分类问题的，但是也有用于多分类问题的版本。SVM还可以扩展到回归问题，这种情况下通常被称为支持向量回归（SVR）。

推导过程可以参考这个视频教程

核

决策边界除了上图的线性核之外，还有多种其他核，这里分别展示各个核的可视化和代码演示：

线性核

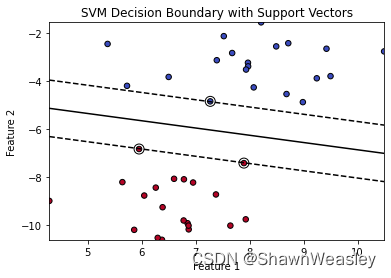
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
from sklearn.datasets import make_blobs

# 我们将创建40个分为两类的数据点
X, y = make_blobs(n_samples=40, centers=2, random_state=6)

# 创建SVM模型 (线性核)
model = svm.SVC(kernel='linear', C=1E10)
model.fit(X, y)

# 得到决策边界
w = model.coef_[0]
b = model.intercept_[0]
x_points = np.linspace(X[:, 0].min(), X[:, 0].max())
y_points = -(w[0] / w[1]) * x_points - b / w[1]

# 绘制数据点
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.coolwarm, s=30, edgecolors='k')

# 绘制决策边界
plt.plot(x_points, y_points, 'k-')

# 绘制间隔边界
margin = 1 / np.sqrt(np.sum(model.coef_ ** 2))
yy_down = y_points - np.sqrt(1 + w[0] ** 2) * margin
yy_up = y_points + np.sqrt(1 + w[0] ** 2) * margin
plt.plot(x_points, yy_down, 'k--')
plt.plot(x_points, yy_up, 'k--')

# 标出支持向量
plt.scatter(model.support_vectors_[:, 0], model.support_vectors_[:, 1],
            s=100, linewidth=1, facecolors='none', edgecolors='k')

# 设定图形属性
plt.gca().set_xlim(x_points[0], x_points[-1])
plt.gca().set_ylim(X[:, 1].min(), X[:, 1].max())
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('SVM Decision Boundary with Support Vectors')

plt.show()

多项式核

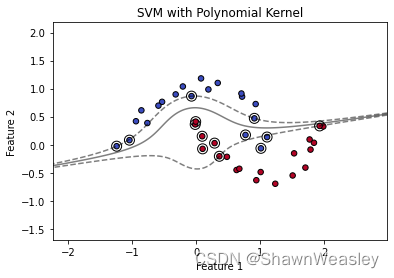
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
from sklearn.datasets import make_moons

# 生成非线性可分的数据集，月牙形数据更适合多项式核
X, y = make_moons(n_samples=40, noise=0.1, random_state=102)

# 创建SVM模型（这里使用多项式核）
model = svm.SVC(kernel='poly', degree=3, C=10)
model.fit(X, y)

# 创建网格以绘制决策边界
grid_x, grid_y = np.meshgrid(np.linspace(X[:, 0].min()-1, X[:, 0].max()+1, 500),
                             np.linspace(X[:, 1].min()-1, X[:, 1].max()+1, 500))

# 计算模型在网格上的决策函数值
Z = model.decision_function(np.c_[grid_x.ravel(), grid_y.ravel()])
Z = Z.reshape(grid_x.shape)

# 绘制决策边界和边距
plt.contour(grid_x, grid_y, Z, colors='k', levels=[-1, 0, 1], alpha=0.5, linestyles=['--', '-', '--'])

# 标出支持向量
plt.scatter(model.support_vectors_[:, 0], model.support_vectors_[:, 1], s=100,
            linewidth=1, facecolors='none', edgecolors='k')

# 绘制数据点
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.coolwarm, s=30, edgecolors='k')

# 设定图形属性
plt.title('SVM with Polynomial Kernel')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()

径向基函数（RBF）核

多项式核通常情况下应用面不是很广，对文本分类等多项式关系高的数据表现会好点，这里相同的数据使用RBF核的效果要好很多，如下图。

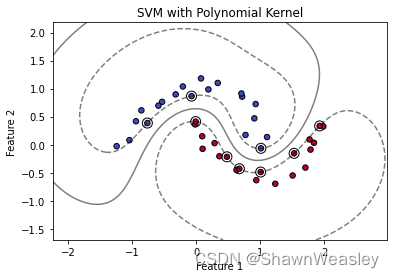
RBF核是一种流行的选择，因为它能够捕捉数据之间的复杂非线性关系，而不需要预先确定转换到高维空间的映射形式。RBF核通常被认为更加“通用”，因为它只有一个调整参数gamma，而且在很多不同的数据集上都能表现出良好的性能。

import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
from sklearn.datasets import make_moons

# 生成非线性可分的数据集，月牙形数据更适合多项式核
X, y = make_moons(n_samples=40, noise=0.1, random_state=102)

# 创建SVM模型（这里使用多项式核）
model = svm.SVC(kernel='rbf', C=1E6)
model.fit(X, y)

# 创建网格以绘制决策边界
grid_x, grid_y = np.meshgrid(np.linspace(X[:, 0].min()-1, X[:, 0].max()+1, 500),
                             np.linspace(X[:, 1].min()-1, X[:, 1].max()+1, 500))

# 计算模型在网格上的决策函数值
Z = model.decision_function(np.c_[grid_x.ravel(), grid_y.ravel()])
Z = Z.reshape(grid_x.shape)

# 绘制决策边界和边距
plt.contour(grid_x, grid_y, Z, colors='k', levels=[-1, 0, 1], alpha=0.5, linestyles=['--', '-', '--'])

# 标出支持向量
plt.scatter(model.support_vectors_[:, 0], model.support_vectors_[:, 1], s=100,
            linewidth=1, facecolors='none', edgecolors='k')

# 绘制数据点
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.coolwarm, s=30, edgecolors='k')

# 设定图形属性
plt.title('SVM with Polynomial Kernel')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()

Sigmoid核

相对而言Sigmoid核并不常用，效果也不太好，这里经过多次调整参数：

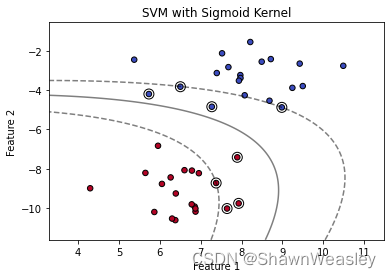
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
from sklearn.datasets import make_blobs


# 我们将创建40个分为两类的数据点
X, y = make_blobs(n_samples=40, centers=2, random_state=6)

# 创建SVM模型（这里使用Sigmoid核）
model = svm.SVC(kernel='sigmoid', C=10, coef0=-0.2)
model.fit(X, y)

# 创建网格以绘制决策边界
grid_x, grid_y = np.meshgrid(np.linspace(X[:, 0].min()-1, X[:, 0].max()+1, 500),
                             np.linspace(X[:, 1].min()-1, X[:, 1].max()+1, 500))

# 计算模型在网格上的决策函数值
Z = model.decision_function(np.c_[grid_x.ravel(), grid_y.ravel()])
Z = Z.reshape(grid_x.shape)

# 绘制决策边界和边距
plt.contour(grid_x, grid_y, Z, colors='k', levels=[-1, 0, 1], alpha=0.5, linestyles=['--', '-', '--'])

# 标出支持向量
plt.scatter(model.support_vectors_[:, 0], model.support_vectors_[:, 1], s=100,
            linewidth=1, facecolors='none', edgecolors='k')

# 绘制数据点
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.coolwarm, s=30, edgecolors='k')

# 设定图形属性
plt.title('SVM with Sigmoid Kernel')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()

总结

支持向量机（SVM）中最常用的核就是径向基函数（RBF）核，通用性较强，拟合效果好，针对一些线性回归的数据可以使用线性核，其他的核都在极小的领域内有应用。