传感器原理与应用--传感器基本特性与应变式传感器
上一篇
传感器的基本特性
一般来说能把特定被测量信息按一定规律转换成某种可用信号的器件或装置,称为传感器
静态特性
-
灵敏度
定义:输出量增量 Δ y \Delta y Δy与引起输出量增量相应输入量 Δ x \Delta x Δx之比
S = Δ y Δ x S = \frac{\Delta y}{\Delta x} S=ΔxΔy? -
线性度
任何传感器都有一定的线性范围,在线性范围内它的输出与输入成比例关系,线性范围越宽,表明传感器的工作量越大。
然而并不能完全是线性的,通常是使用拟合直线来拟合原来的曲线
因此线性度是指传感器的实际输入-输出曲线与拟合直线之间的吻合程度。
实际曲线与它的两个端尖连线之间的偏差称为非线性误差,取其中到的最大偏差与满量程之比称为线性度
γ L = + Δ L m a x Y F S ? 100 % \gamma_L = \frac{+}{} \frac{\Delta L_{max}}{Y_{FS}} *100\% γL?=+?YFS?ΔLmax???100%

-
迟滞
传感器在相同工作条件下,输入量由小到大(正行程)及输入量由大到小(反行程)(正反行程)变化期间其输入输出特性曲线不重合的现象称为迟滞。
不相同的差值称为迟滞差值,记最大迟滞差值为 Δ H m a x \Delta H_{max} ΔHmax?与满量程输出值 Y F S Y_{FS} YFS? 之比称为迟滞误差
γ H = Δ H m a x Y F S ? 100 % \gamma_H = \frac{\Delta H_{max}}{Y_{FS}} * 100\% γH?=YFS?ΔHmax???100% -
重复性
重复多次测量,结果不一样。
重复性误差属于随机误差。常用标准差 σ \sigma σ计算,也可用正反行程中最大重复差值 Δ R m a x \Delta R_{max} ΔRmax?计算
γ = + Δ R m a x Y F S ? 100 % \gamma = \frac{+}{} \frac{\Delta R_{max}}{Y_{FS}} * 100\% γ=+?YFS?ΔRmax???100% -
漂移
输入量不变的情况下,传感器输出量会随时间变化,此现象称为漂移
通常用工作环境偏离标准环境( 2 0 o C 20^oC 20oC)时,温度变化 1 o C 1^oC 1oC输出值的变化量与满量程 Y F S Y_{FS} YFS?的百分比表示 温漂 = y t ? y 20 Y F S ? Δ t ? 100 % 温漂 = \frac{y_t - y_{20}}{Y_{FS} * \Delta t} * 100 \% 温漂=YFS??Δtyt??y20???100%
动态特性
输出量会随输入的变化而有一定的滞后性
-
零阶系统
具有理想的动态特性,无论被测量如何随时间变化,零阶系统的输出都不会失真,其输出在时间上也无任何滞后,所以也称为比例系统 -
一阶系统
微分方程
τ d y ( t ) d t + y ( t ) = k x ( t ) \tau \frac{dy(t)}{dt} + y(t) = kx(t) τdtdy(t)?+y(t)=kx(t)
传感器的时间常数 τ \tau τ 具有时间量纲,它反应传感器惯性的大小(滞后性),通常 τ \tau τ 越小反应越快,通常情况下当时间达到 4 τ 4\tau 4τ 左右,就可以认为达到了稳定 -
二阶系统
微分方程
d 2 y ( t ) d t 2 + 2 ξ ω n d y ( t ) d t + ω n 2 y ( t ) = ω n 2 k x ( t ) \frac{d^2y(t)}{dt^2} + 2\xi\omega_n\frac{dy(t)}{dt} + \omega_n^2y(t) = \omega_n^2kx(t) dt2d2y(t)?+2ξωn?dtdy(t)?+ωn2?y(t)=ωn2?kx(t)
k是静态灵敏度, ξ \xi ξ 是阻尼系数, ω n \omega_n ωn?是固有频率
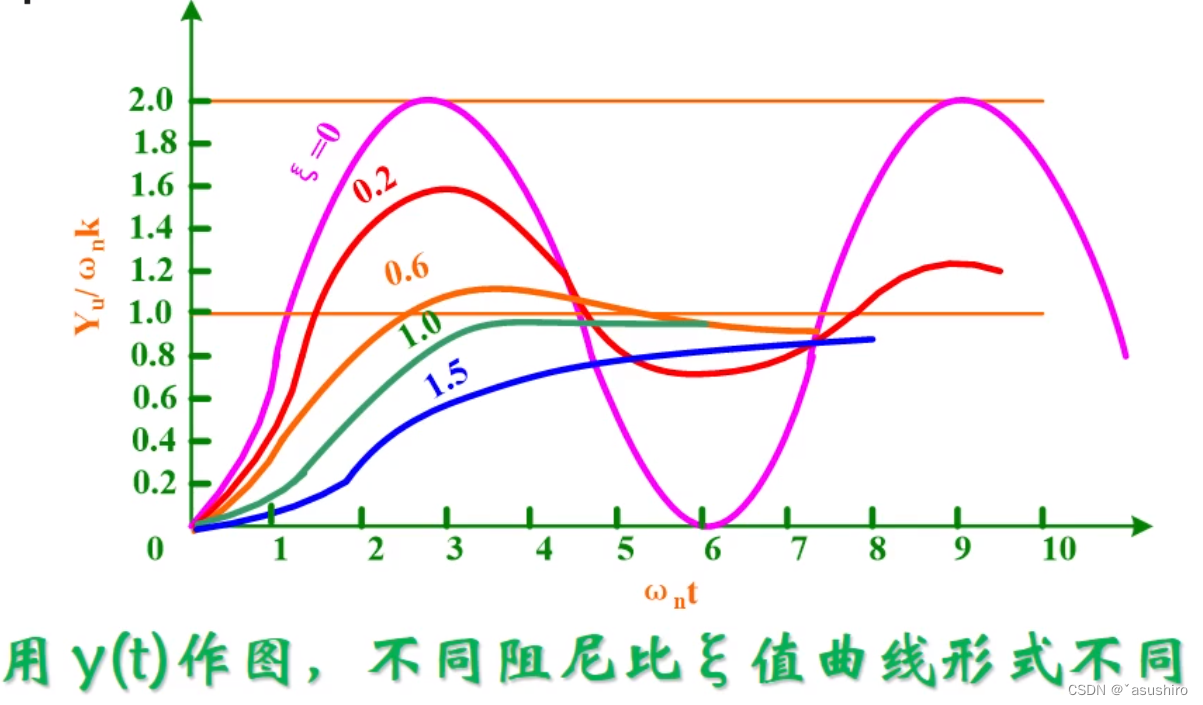
- 当
ξ
=
0
\xi = 0
ξ=0时,这种等幅振荡状态称为无阻尼状态,
永远达不到稳定 - 当
ξ
>
1
\xi > 1
ξ>1时,这种不振荡的衰减过程称为过阻尼状态,
稳定时间较长 - 当
ξ
=
1
\xi = 1
ξ=1时, 他是从振荡衰减到不振荡过渡的临界状态称为临界阻尼状态,
响应时间最短 - 当
0
<
ξ
<
1
0 < \xi < 1
0<ξ<1时,是衰减振荡的过程,根据
ξ
\xi
ξ 的不同衰减的快慢也不同,称为欠阻尼状态,
随着ξ \xi ξ的下降稳定时间加长
阻尼比越大曲线的衰减越大
通常实际过程中按欠阻尼调整一般取 ξ \xi ξ = 0.6 ~ 0.7, 这样达到稳定的时间最短
而 ω n \omega_n ωn?也是等幅振荡频率,越高系统的相应越快
通常传感器的固有频率至少应大于被测信号频率的3~5倍 ω n > = ( 3 ? 5 ) ω \omega_n >= (3-5) \omega ωn?>=(3?5)ω, - 当
ξ
=
0
\xi = 0
ξ=0时,这种等幅振荡状态称为无阻尼状态,
应变式传感器
工作原理是电阻应变效应,导体在外界作用下产生机械形变,其阻值相应发生变化。
优点:精度高,响应时间非常快
一根金属电阻丝电阻:
R
=
ρ
?
l
S
R = \frac{\rho *l}{S}
R=Sρ?l?
- ρ \rho ρ为电阻丝电阻率
- l l l 为电阻丝长度
- S 为电阻丝截面积
将一个电阻丝拉长后,长度增加,截面积减小,电阻增大
将单位应变引起的电阻值变化称为电阻丝的灵敏度系数
K
K
K,物理意义是单位应变所引起的电阻相对变化量
灵敏度的影响因素:1. 应变片受力后材料的集合尺寸的变化 2. 应变片受力后材料的电阻率的变化
半导体材料的灵敏度更高,但是受温度影响大,稳定性不高
同时应变片还具有的特性:
F
=
E
?
?
F = E * \epsilon
F=E??
力的大小 = 弹性模量 * 形变大小
金属电阻应变片的结构
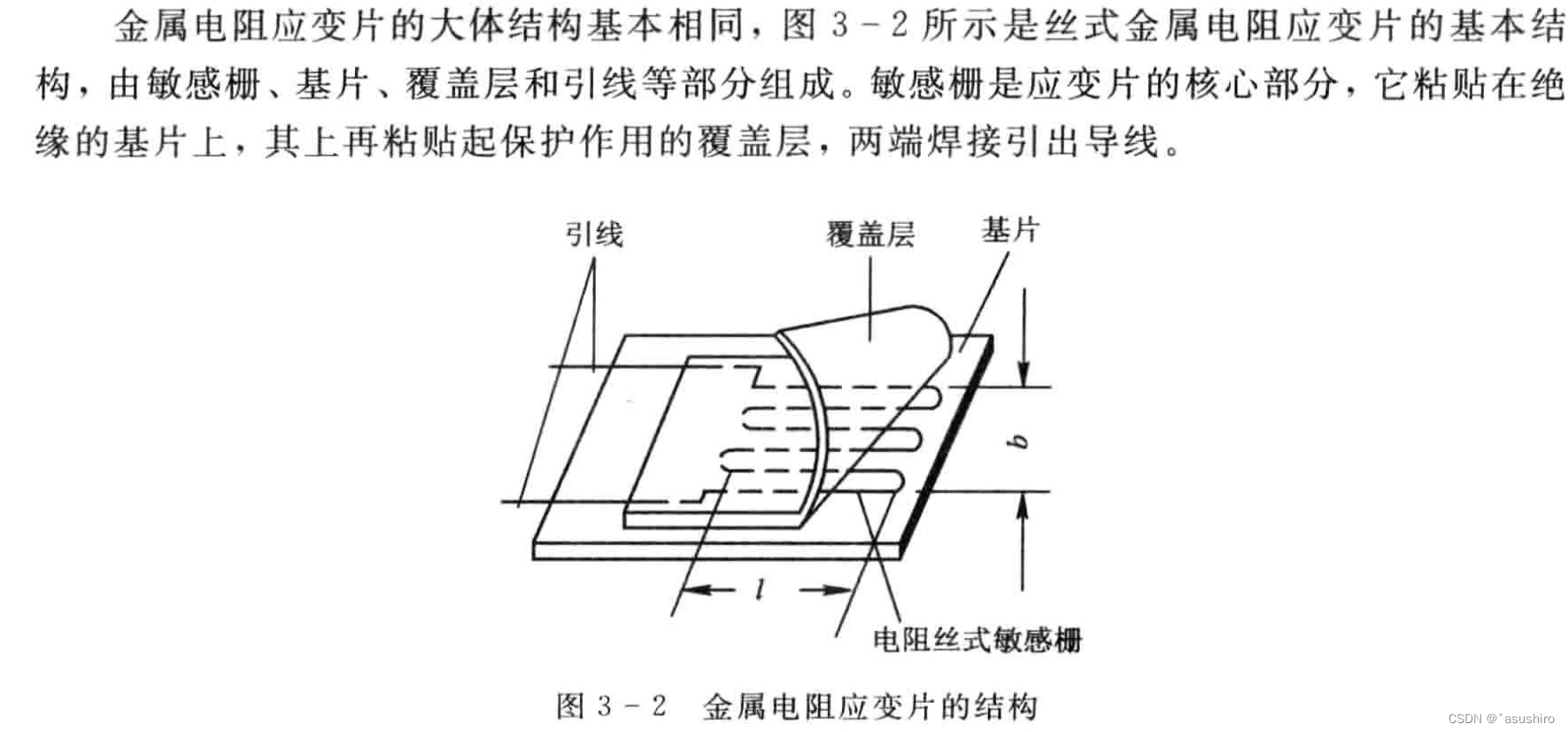
金属应变片的基本特性
-
灵敏系数:
K = Δ R R ? ? K = \frac{\Delta R}{R* \epsilon} K=R??ΔR?
电阻的变化率除以形变的大小 -
横向效应
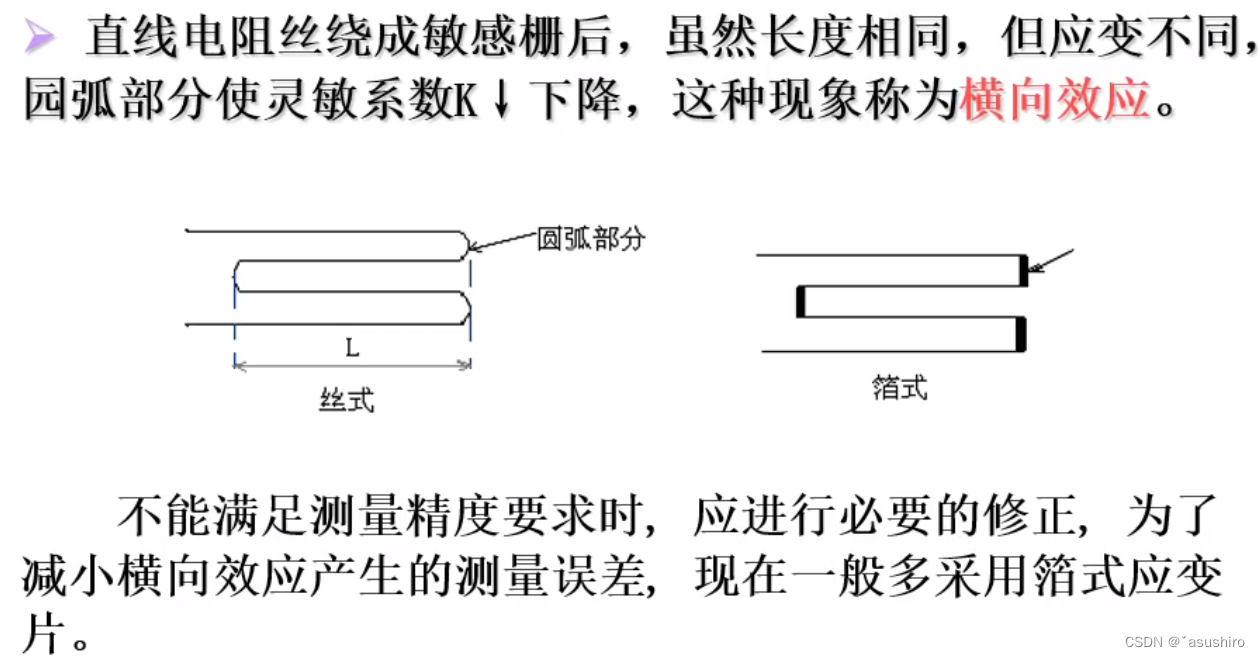
将端点做的更宽 -
应变片的温度误差及补偿
温度会影响电阻温度系数,同时由于环境温度的变化,电阻丝会产生附加变形,从而产生附加电阻的变化
温度补偿的方法:线路补偿法,应变片自补偿
线路补偿法
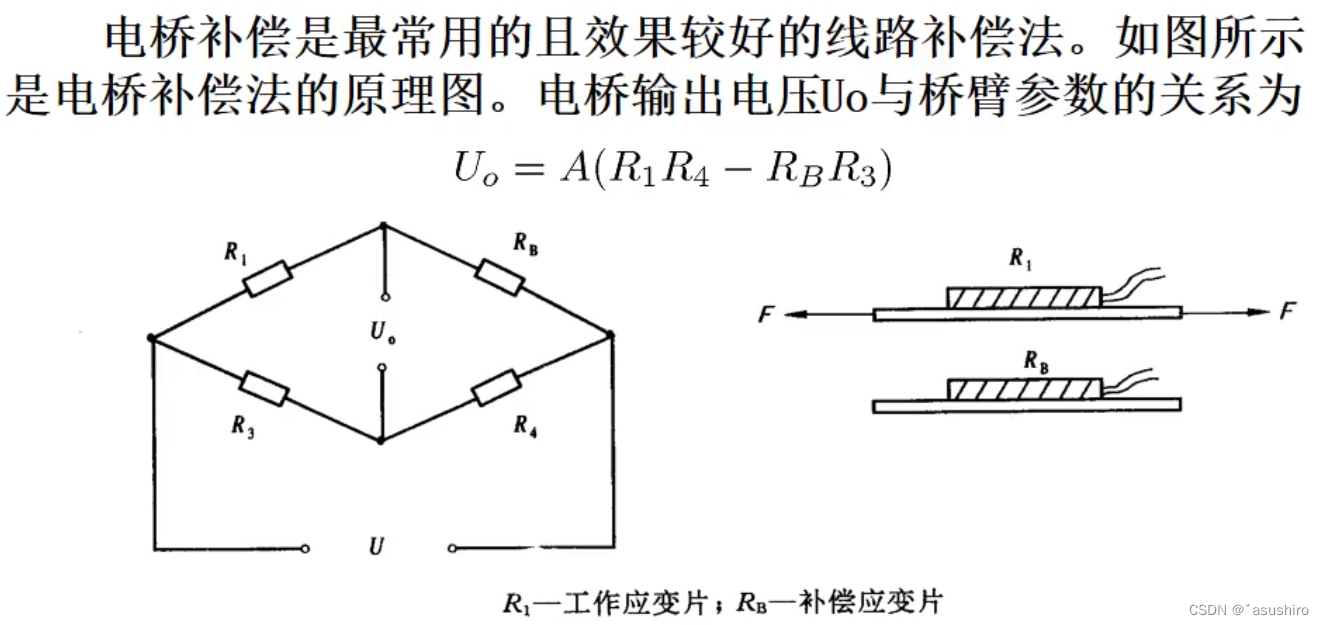
必须满足的条件:R3和R4的阻值相同,R1与
R
B
R_B
RB?的参数相同,两个应变片在同一温度场
电阻应变片的测量电路:
- 直流单臂电桥
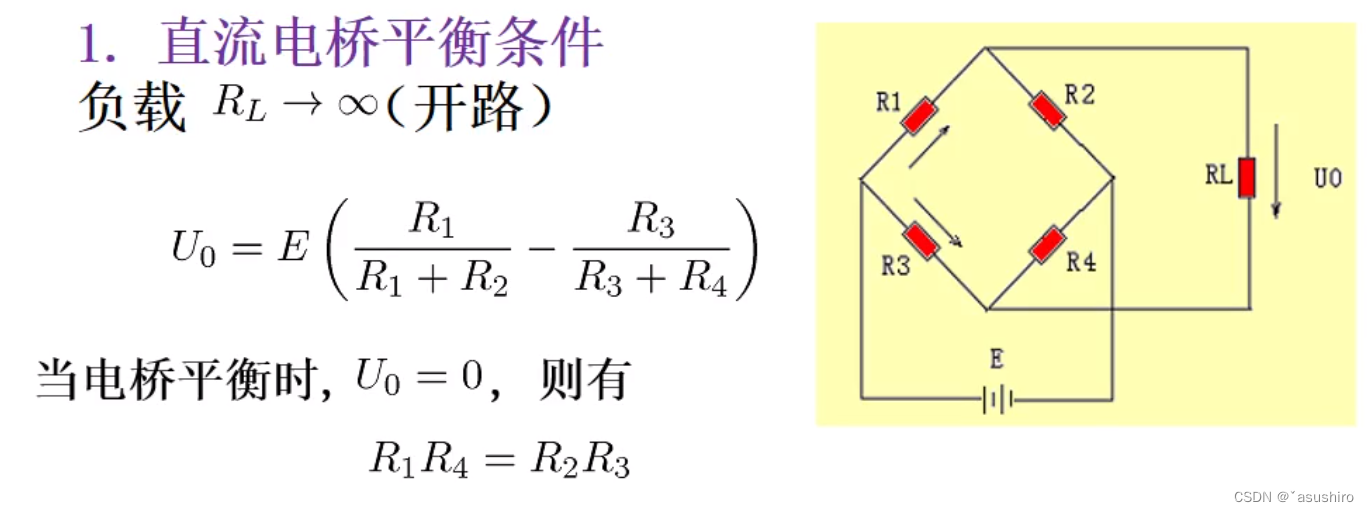
有向更好的测量阻值的变化,当是等臂电桥( R 1 = R 2 = R 3 = R 4 R_1 = R_2 = R_3 = R_4 R1?=R2?=R3?=R4?)是电压灵敏度最高
此时:
电压为 U 0 = E 4 ? Δ R 1 R 1 电压为U_0 = \frac{E}{4}*\frac{\Delta R_1}{R_1} 电压为U0?=4E??R1?ΔR1??
电压灵敏度为 K U = E 4 电压灵敏度为K_U = \frac{E}{4} 电压灵敏度为KU?=4E?
但是这个公式在推导的过程中由于舍弃了一项,所以结果是有一点误差的,差动形式,进行抵消了,所以没有误差
-
半桥差动电桥

注意:应变片是一边增大,另一边减小,刚好放在受力片的上下,一端延伸,一端压缩,正好相反
电压为 U 0 = E 2 ? Δ R 1 R 1 电压为U_0 = \frac{E}{2} * \frac{\Delta R_1}{R_1} 电压为U0?=2E??R1?ΔR1??
电压灵敏度为 K U = E 2 电压灵敏度为K_U = \frac{E}{2} 电压灵敏度为KU?=2E? -
全桥差动电桥

同时要保证上下是增减,左右是增减的
其中一种接法是,将 R 1 , R 4 R_1,R_4 R1?,R4?接在受力片上面,将 R 2 , R 3 R_2, R_3 R2?,R3?接在受力片的下面,就是将对角的接在同一面
电压 U 0 = E ? Δ R 1 R 1 电压U_0 = E* \frac{\Delta R_1}{R_1} 电压U0?=E?R1?ΔR1??
电压灵敏度 K U = E 电压灵敏度K_U = E 电压灵敏度KU?=E
优点:无线性误差,灵敏度更高,有温度补偿作用
应变式传感器的应用
-
测量力的大小
- 悬臂梁式力传感器
等截面梁传感器

形变与力的大小、梁伸长的长度成正比
与梁的厚度的平方、弹性模量(材料强度)成反比 - 等强度梁力传感器

当相同的里作用在截面的任何地方,产生的形变相同
- 悬臂梁式力传感器
-
测量加速度
凡是能与力有关的物理量都可以通过转换进行测量

下一篇
未完待续
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!