2005年AMC8数学竞赛中英文真题典型考题、考点分析和答案解析

今天距离2024年的AMC8美国数学竞赛举办已不足一个月了，赶紧利用周末的时间刷刷真题，查漏补缺吧！如果您有任何关于AMC8比赛的任何问题都可以问我，关于题目的解析也可以交流。

今天我们来看看2005年AMC8竞赛的五道典型考题。欢迎您查看历史文章了解之前各年的真题解析，本系列会持续更新，直到大家参加完2024年的比赛。

好消息！为帮助孩子们更便捷地做真题，六分成长独家将AMC8竞赛2000-2023年的所有真题制作了在线版本，适合各种终端和设备利用碎片化时间，快速、反复做题，提高最后一个月的备考效率，而且这些真题文档和在线练习题会不断更新。

2005年AMC8数学竞赛真题、考点和解析：第3题

这道题的考点是平面几何的轴对称。

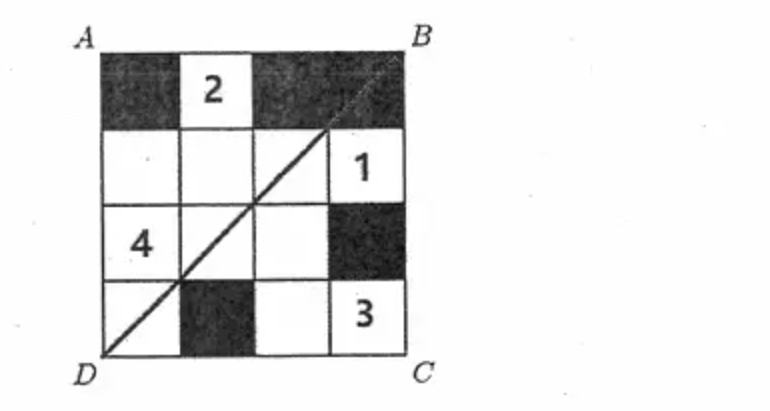
如下图所示，为使得图形关于BD对称，则编号为1,2,3,4的方块均需要被涂成黑色，因此总共4个，选D。这种题目需要有一定的空间（平面）想象力，建议在图上，或者电脑上截图画一画，比较快。

2005年AMC8数学竞赛真题、考点和解析：第8题

这道题的考点是数论之奇数和偶数。

直接对各个选项逐个分析：

• 选项A：因为m是奇数，3n也是奇数，那么m+3n就是偶数。
• 选项B：因为3m和n都是奇数，所以3m-n是偶数。
• 选项C：m是奇数，那么m的平方也是奇数，3*m的平方也是奇数，所以两项相加是偶数。
• 选项D：因为n*m和3都是奇数，所以n*m+3是偶数，则(n*m+3)的平方也为偶数。
• 选项E：因为m和n都是奇数，所以3*m*m也是奇数。符合题意，所以这道题选E。

六分成长提醒：这道题目需要了解奇数、偶数的一些特点和性质，如果记不住也没关系，直接假设mn分别为1和3，代入各个选项用排除法也很快。

2005年AMC8数学竞赛真题、考点和解析：第12题

这道题的考点是等差数列，

假设5月5日这天吃了x根香蕉，则从5月5日到5月1日，依次吃了x,x-6x-12,x-18,x-24根香蕉，它们和为100，即x+（x-6）+（x-12）+（x-18）+（x-24）=100。化简为，5x=160，x=32，选D。

六分成长提醒：这种题目也可以直接将选项往里面代入计算，先去中间值30，然后根据计算的结果再代入另一个，也能很快得到答案。这就是选择题的好处。

2005年AMC8数学竞赛真题、考点和解析：第20题

这道题的考点是数论的倍数。

假设经过m个回合后，他们停在同一个点上，则Alice总共顺时针移动了5m个点，而Bob总共逆时针移动了9m个点，因为他们停在同一个点上，所以他们移动的总点数是12的倍数，即5m+9m=14m需要是12的倍数。因为14有2这个因子，所以m必须有6这个因子，m最小为6。所以选A。

2005年AMC8数学竞赛真题、考点和解析：第25题，压轴题

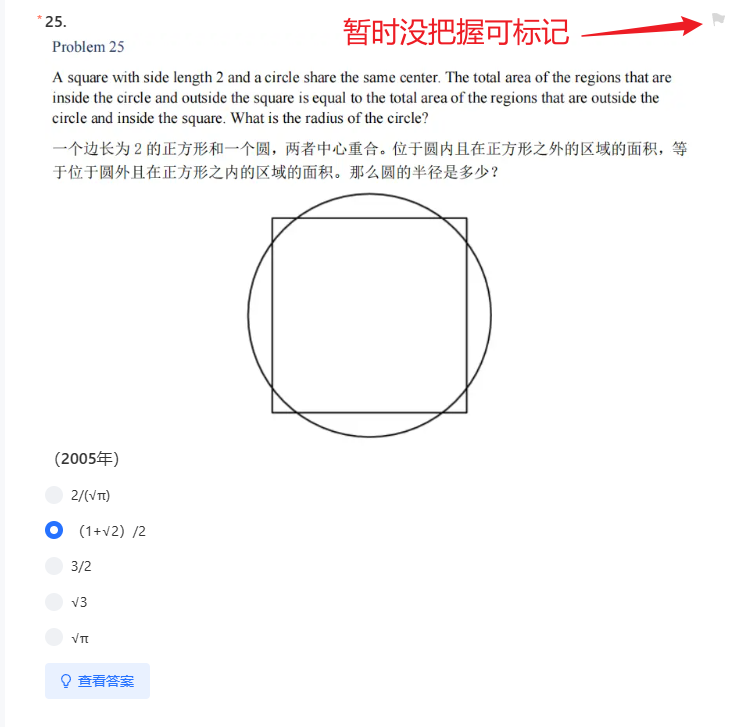
这道题的考点是平面几何的面积。

如上图，在圆内而在正方形之外的区域是图中4块黑色月牙形区域。而在正方形内圆之外的区域如图中灰色部分所示。这2部分面积相等，意味着黑色区域从面积上恰好可以填充灰色区城，也即：圆的面积等于正方形面积。所以πr^2=2^2，计算这个算式：

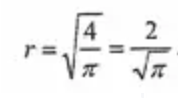
六分成长提醒：这道题目看起来很复杂，想明白了其实很简单。不要被压轴题吓坏了，因为AMC8竞赛的时间有限，所以题目往往不会很偏、很钻，多思考一些巧的方法，寻找规律。当然了，这些都是建立在对题目熟悉的基础上。

六分成长针对2024年AMC8备考资源

为帮助孩子更好地复习和备考AMC8竞赛，六分成长独家制作了丰富的在线练习真题集和备考文档、视频资料。无论孩子是参加了机构培训班作为辅助学习资源，还是完全自学（实践证明是可行的），都能大幅提高效率。如果您兴趣，欢迎私信与我沟通和交流。

科学备考，利用碎片化时间再冲刺二十多天，收获好成绩！

加油！