Batch Normalization（BN）批量归一化

[1502.03167] Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift (arxiv.org)

1.研究背景

????????深度神经网络的训练过程中，每一层输入数据的分布可能会随着网络参数的更新而发生变化，这种现象被称为内部协变量偏移（Internal Covariate Shift）。这会使得每一层网络需要不断适应新的输入分布，增加了训练的复杂性。

? ? ? ? BN通过对神经网络每一层的输入进行标准化处理来解决内部协变量偏移和梯度问题。其基本思想是将每一层的输入进行线性变换和缩放，使得输出值分布均值为0，方差为1。

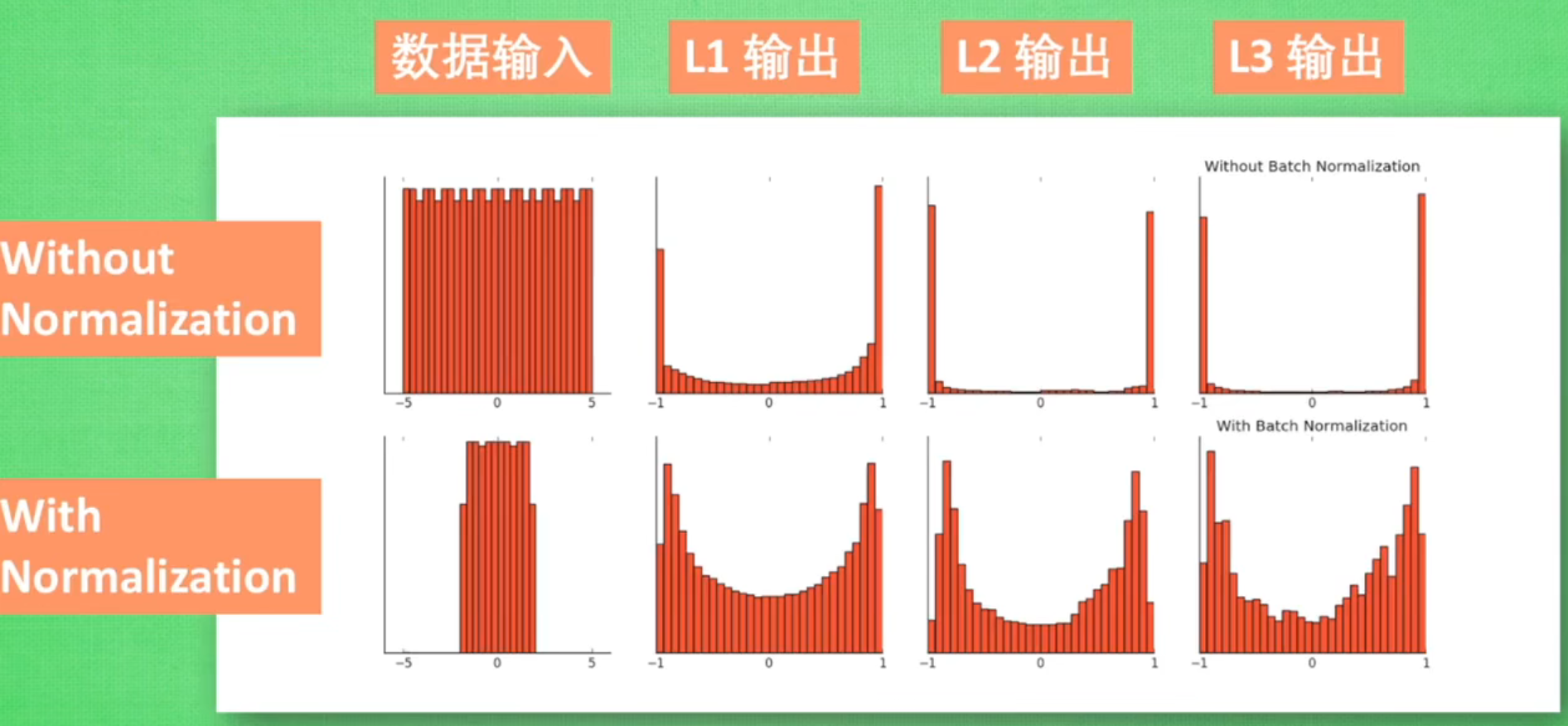
????????同时还可以使Sigmoid和tanh能够更好传递梯度，避免梯度消失和梯度爆炸。

????????

?2.BN是如何操作的

2.1 训练阶段

????????Batch normalization 在训练过程中对每个 mini-batch（小批量数据）的输入进行处理，BN层通常在全连接层/卷积层的后面，激活函数的前面，主要包括以下步骤：

1. 计算均值和方差：对于每个 mini-batch，在每一层的输入数据上计算均值和方差。

2. 标准化处理：使用计算得到的均值和方差对该 mini-batch 的输入进行标准化处理，即将输入数据减去均值，并除以方差。这一步骤使得输入数据的分布接近标准正态分布。

3. 缩放和平移：对标准化后的数据进行缩放和平移操作，通过乘以一个学习得到的参数（缩放因子）并加上另一个学习得到的参数（偏移量），以便让网络能够学习到更合适的BN的程度即表示。

对于输入数据 x，在 Batch normalization 中，其处理过程如下：

????????????????????????????????????????????????????????????????????

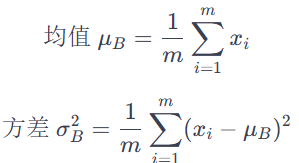
其中，m 是 mini-batch 的大小，是 mini-batch 中的每个样本。

标准化处理：

???????????????????????????????????????????????????????????????????????????????????????????????????

其中，? 是为了数值稳定性而添加的小常量，避免除以零的情况。?

缩放和平移：

其中，γ 是缩放因子，β 是偏移量，都是可以学习的参数

????????在训练过程中，缩放因子 γ 和偏移量 β 通过梯度下降等优化算法进行学习，以最大程度地提高网络的表征能力和性能。

2.2 测试阶段

????????在训练阶段，Batch Normalization 对每个 mini-batch 的均值和方差进行估算并进行标准化处理。而在测试阶段，不同于训练阶段，模型通常需要对单个样本进行推断，因此无法计算均值和方差，而需采用训练数据对应的全局均值和方差。全局均值和方差的计算，可采用无偏估计和移动平均两种方法，两种方法各有优缺点。

2.2.1 无偏估计

????????训练过程包括多个batch，每个batch对应一个均值和方差，因此可采用统计学上无偏估计的方法来计算训练数据的全局均值和方差，测试阶段直接使用训练数据的全局均值和方差，根据下面式子计算。无偏估计法需要保留训练时所有batch的均值和方差，计算准确，但存储资源消耗大。

??????????????????????????????????????????????????????????????????????????????????????????

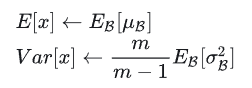
? ? ? ??分别为训练阶段所有batch均值和方差的期望（均值）

2.2.2?移动平均

????????为了节省存储资源，实际中大多采用移动平均的方式来计算全局的均值和方差。移动平均的计算过程如下面式子所示，每次batch训练后对全局的均值和方差进行更新，其中 λ为在 0 到 1 之间的衰减系数，用于控制历史统计信息对移动平均值的贡献程度，值越大，更新速度越慢，过程越稳定。

????????这种方式只需保留三个值，全局统计值、当前batch的统计值和衰减系数，消耗的存储资源少，在损失一定准确度的情况下，计算速度快，在训练阶段可同步完成总统计值的计算，不需额外的计算。

3.使用BN的优势

1. 加快训练收敛速度
2. 可以使用更大的学习率
3. 对权重初始化不敏感
4. 可以不使用dropout

4.在Pytorch中使用BN

????????Pytorch已经为我们实现BN，只需要调用nn.BatchNorm1d，nn.BatchNorm2d，nn.BatchNorm3d，传入上一层的通道数即可。BN也相当于一层。

? ? ? ? 全连接层神经网络中全连接层使用nn.BatchNorm1d

class NeuralNetwork(nn.Module):
    def __init__(self):
        super(NeuralNetwork, self).__init__()
        self.fc1 = nn.Linear(784, 256)  # 输入层到隐藏层
        self.bn1 = nn.BatchNorm1d(256)  # BatchNorm1d 对隐藏层的输出进行批标准化
        self.relu = nn.ReLU()  # 激活函数
        self.fc2 = nn.Linear(256, 10)  # 隐藏层到输出层

    def forward(self, x):
        x = self.fc1(x)
        x = self.bn1(x)
        x = self.relu(x)
        x = self.fc2(x)
        return x

? ? ? ? 卷积神经网络中卷积层使用nn.BatchNorm2d

class CNN(nn.Module):
    def __init__(self):
        super(CNN, self).__init__()
        self.conv1 = nn.Conv2d(in_channels=3, out_channels=16, kernel_size=3, stride=1, padding=1)  # 卷积层
        self.bn1 = nn.BatchNorm2d(16)  # 对卷积层输出进行批标准化
        self.relu = nn.ReLU()  # 激活函数
        self.pool = nn.MaxPool2d(kernel_size=2, stride=2)  # 池化层
        self.fc = nn.Linear(16 * 16 * 16, 10)  # 全连接层

    def forward(self, x):
        x = self.conv1(x)
        x = self.bn1(x)
        x = self.relu(x)
        x = self.pool(x)
        x = x.view(-1, 16 * 16 * 16)  # 将特征展平为一维
        x = self.fc(x)
        return x