EMD、EEMD、FEEMD、CEEMD、CEEMDAN的区别、原理和Python实现（五）CEEMDAN

目录

前言

1 完全自适应噪声集合经验模态分解CEEMDAN介绍

1.1 CEEMDAN简介

1.2 CEEMDAN主要特点

2 CEEMDAN分解的步骤

3?基于Python的CEEMDAN实现

3.1 导入数据

3.2 CEEMDAN分解

3.3 信号分量的重构

3.4 信号分量的处理

3.5 CEEMDAN优缺点

---

往期精彩内容：

风速预测（一）数据集介绍和预处理-CSDN博客

风速预测（二）基于Pytorch的EMD-LSTM模型-CSDN博客

风速预测（三）EMD-LSTM-Attention模型-CSDN博客

风速预测（四）基于Pytorch的EMD-Transformer模型-CSDN博客

风速预测（五）基于Pytorch的EMD-CNN-LSTM模型-CSDN博客

风速预测（六）基于Pytorch的EMD-CNN-GRU并行模型-CSDN博客

前言

本文基于前期介绍的风速数据（文末附数据集），进行完全自适应噪声集合经验模态分解（CEEMDAN）的介绍与参数选择，最后通过Python实现对风速数据的CEEMDAN分解。风速数据集的详细介绍可以参考下文：

风速预测（一）数据集介绍和预处理-CSDN博客

Python 中 CEEMDAN包的下载安装：

# 下载
pip install EMD-signal

# 导入
from PyEMD import CEEMDAN

切记，很多同学安装失败，不是pip install EMD，也不是pip install PyEMD， 如果 pip list 中 已经有 emd，emd-signal，pyemd包的存在，要先 pip uninstall 移除相关包，然后再进行安装。

1 完全自适应噪声集合经验模态分解CEEMDAN介绍

1.1 CEEMDAN简介

针对 EMD 算法分解信号存在模态混叠的问题，EEMD 和 CEEMD 分解算法通过在待分解信号中加入随机白噪声来减轻 EMD 分解的模态混叠，但是这两种算法分解信号得到的模态分量中总会残留一定的白噪声，并且信号加噪声经EMD分解可能会产生不同数量的模态， 这将影响后续信号的分析和处理，为了解决这些问题，TORRES 等提出了一种改进算法— —完全自适应噪声集合经验模态分解（CEEMDAN）。

1.2 CEEMDAN主要特点

CEEMDAN 分解从两个方面解决了上 述问题：

• 每次迭代加入经 EMD 分解后含辅助噪声的 IMF 分量；?

• EEMD 分解和 CEEMD 分解是将经验模态分解后得到的模态分量进行总体平均， CEEMDAN 分解则在得到的第一阶 IMF 分量后就进行总体平均计算，得到最终的第一阶 IMF 分量，然后对残余部分重复进行如上操作，这样便有效地解决了白噪声从高频到低频的转移传递问题。

2 CEEMDAN分解的步骤

(1) EEMD 方法是将添加白噪声后的 M 个信号直接做 EMD 分解，然后相对应的 IMF 间直接 求均值。

(2) CEEMDAN 方法是每求完一阶 IMF 分量，又重新给残值加入白噪声（或白噪声的 IMF 分 量）并求此时的 IMF 分量均值，并逐次迭代。

3?基于Python的CEEMDAN实现

3.1 导入数据

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
matplotlib.rc("font", family='Microsoft YaHei')

# 读取已处理的 CSV 文件
df = pd.read_csv('wind_speed.csv' )
# 取风速数据
winddata = df['Wind Speed (km/h)'].tolist()
winddata = np.array(winddata) # 转换为numpy
# 可视化
plt.figure(figsize=(15,5), dpi=100)
plt.grid(True)
plt.plot(winddata, color='green')
plt.show()

3.2 CEEMDAN分解

from PyEMD import CEEMDAN

# 创建 CEEMDAN 对象
ceemdan = CEEMDAN(trials=100, epsilon=0.005)
# NE=100 epsilon=0.005(信噪比)

# 对信号进行 CEEMDAN分解
IMFs = ceemdan(winddata)

# 可视化
plt.figure(figsize=(20,15))
plt.subplot(len(IMFs)+1, 1, 1)
plt.plot(winddata, color='hotpink')
plt.title("原始信号")

for num, imf in enumerate(IMFs):
    plt.subplot(len(IMFs)+1, 1, num+2)
    plt.plot(imf, color='c')
    plt.title("IMF "+str(num+1), fontsize=10)
# 增加第一排图和第二排图之间的垂直间距
plt.subplots_adjust(hspace=0.8, wspace=0.2)
plt.show()

参数：

• trials：迭代次数（集总平均次数），默认100

• epsilon：信噪比，默认0.005

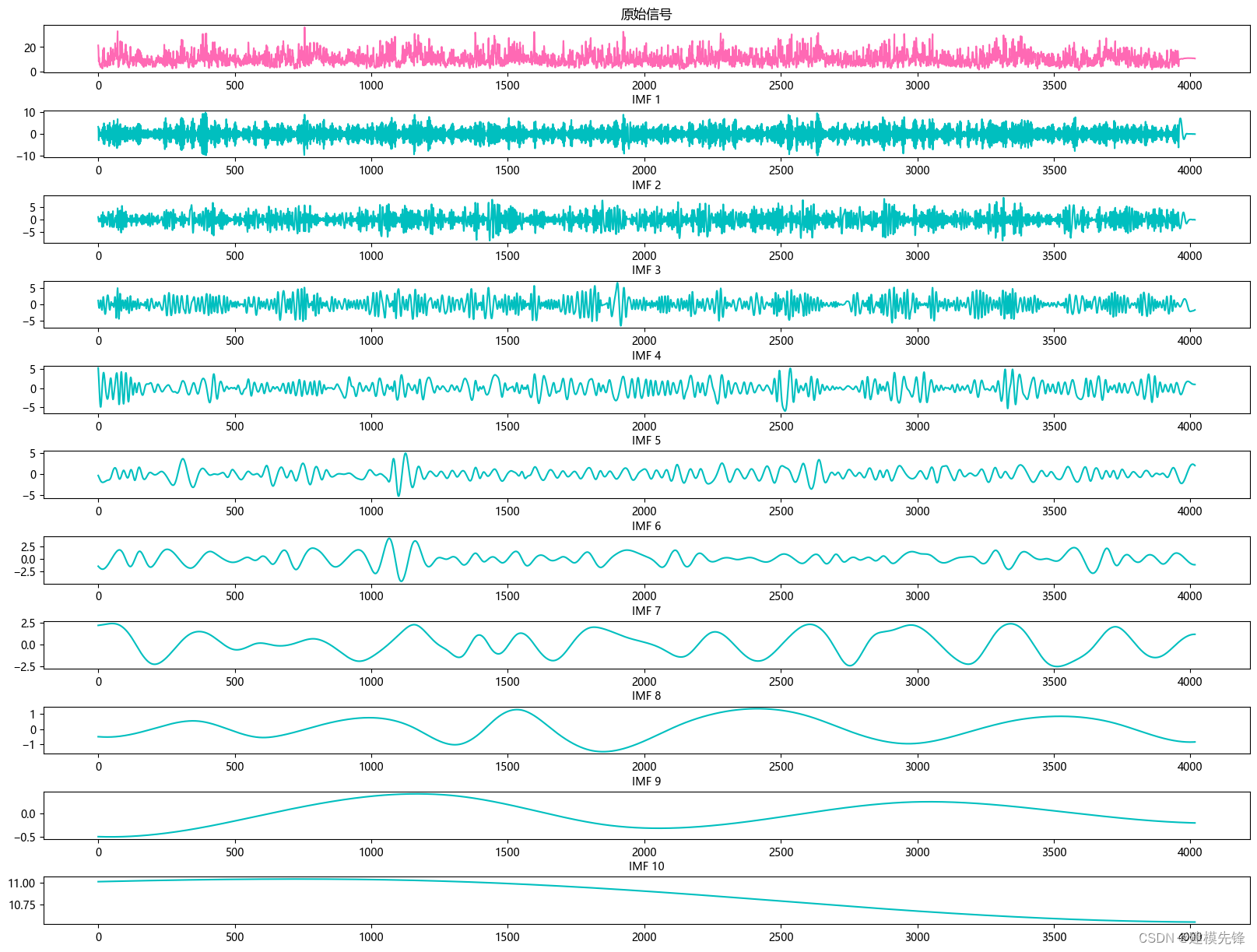
3.3 信号分量的重构

# 分量重构
reconstructed_data = np.sum(IMFs, 0) # 沿ｙ轴方向求和

plt.figure(figsize=(15,5))
plt.plot(winddata, linewidth=1, color='hotpink', label='PM2.5')
plt.plot(reconstructed_data, linewidth=1, color='c', label='分解重构结果')
plt.title("CEEMDAN 分解重构结果", fontsize=10, loc='center')
plt.xticks(fontsize=10) # x 轴刻度字体大小
plt.yticks(fontsize=10) # y 轴刻度字体大小
plt.legend(loc='upper right') # 绘制曲线图例，信息来自类型 label
plt.show()

对比 EMD 重构：

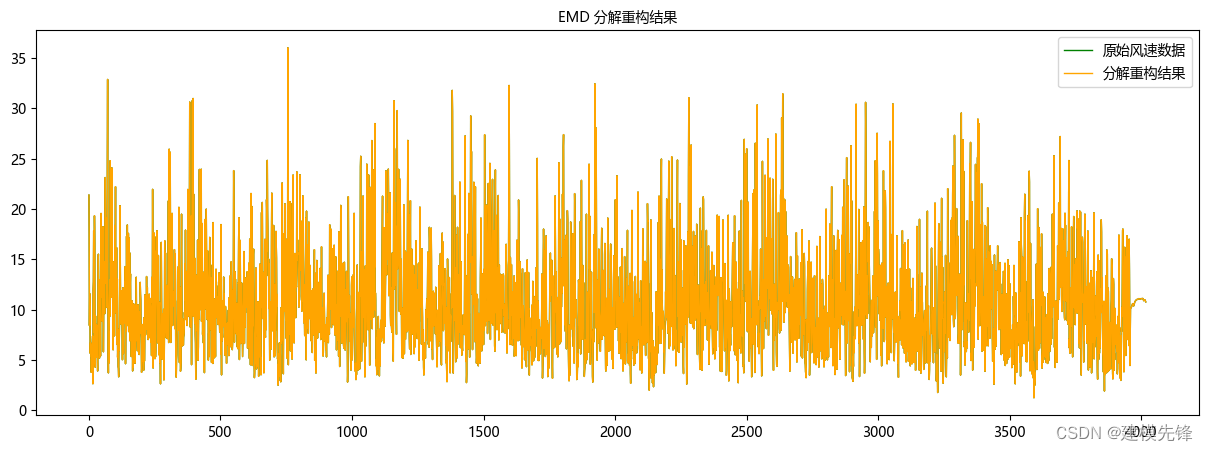
CEEMDAN分解重构效果明显好于EMD!

3.4 信号分量的处理

通过完全自适应噪声集合经验模态分解（CEEMDAN）得到了信号的分量，可以进行许多不同的分析和处理操作，以下是一些常见的对分量的利用方向：

（1）信号重构：将分解得到的各个本征模态函数（IMF）相加，可以重构原始信号。这可以用于验证分解的效果，或者用于信号的重建和恢复。

（2）去噪：对于复杂的信号，可能存在噪声或干扰成分。通过分析各个IMF的频率和振幅，可以识别和去除信号中的噪声成分。

（3）频率分析：分析每个IMF的频率成分，可以帮助理解信号在不同频率上的振荡特性，从而揭示信号的频域特征。

（4）特征提取：每个IMF代表了信号的局部特征和振荡模式，可以用于提取信号的特征，并进一步应用于机器学习或模式识别任务中。

（5）信号预测：通过对分解得到的各个IMF进行分析，可以探索信号的未来趋势和发展模式，从而用于信号的预测和预测建模。

（6）模式识别：分析每个IMF的时域和频域特征，可以帮助对信号进行模式识别和分类，用于识别信号中的不同模式和特征。

（7）异常检测：通过分析每个IMF的振幅和频率特征，可以用于探测信号中的异常或突发事件，从而用于异常检测和故障诊断。

在得到了信号的分量之后，可以根据具体的应用需求选择合适的分析和处理方法，以实现对信号的深入理解、特征提取和应用。

3.5 CEEMDAN优缺点

优点：

• 完备性，即把分解后的各个分量相加能够获得原信号的性质。?

• 更快的计算速度，正是由于上一条，相较于 EEMD 该方法不需要太多的平均次数，可以 有效提升程序运算速度。?

• 更好的模态分解结果，EEMD 分解可能会出现多个幅值很小的低频 IMF 分量，这些分量 对于信号分析意义不大，CEEMDAN 方法可以减少这些分量数目。

• 解决了 EEMD 算法中会出现不同模态数量的问题。

缺点：

• 模态中仍包含一些残余噪声；

• 与 EEMD 相比，在分解的早期阶段存在一些“伪”模态，即前两种或三种模式包含大量的相 似噪声和类似的信号尺度(ICEEMDAN 解决了该问题)；

• 利用 CEEMDAN 算法分解含噪声信号时，若将含噪声较多的 IMF 分量直接舍弃，容易造 成有效信息的缺失

参考文献

[1]《非平稳数据分解理论 ?从入门到实践》.蒋锋,杨华.中国财政经济出版社.