求解最大子段和问题

求解最大子段和问题。

对于给定序列a1,a2,a3……an,寻找它的某个连续子段，使得其和最大。如( -2,11,-4,13,-5,-2 )最大子段是{ 11,-4,13 }其和为20。

要求：分别用教材所给的三种方法求解（简单方法、分治法、动态规划），通过实例比较结果和时间效率。

提交内容：算法的思想、程序源代码及其说明、实例运行结果及分

简单方法求解：

以a[0]开始: {a[0]}, {a[0],a[1]},{a[0],a[1],a[2]}……{a[0],a[1],……a[n]}共n个

以a[1]开始: {a[1]}, {a[1],a[2]},{a[1],a[2],a[3]}……{a[1],a[2],……a[n]}共n-1个

……

以a[n]开始:{a[n]}共1个

暴力破解方法简单直观，通过两层嵌套循环遍历所有可能的子段，计算它们的和，并保留最大和。这种方法的时间复杂度为O(n^2)，适用于小规模数据集。

分治方法：

将序列a[1:n]分成长度相等的两段a[1:n/2]和a[n/2+1:n],分别求出这两段的最大字段和，则a[1:n]的最大子段和有三中情形：

a[1:n]的最大子段和与a[1:n/2]的最大子段和相同；

a[1:n]的最大子段和与a[n/2+1:n]的最大子段和相同；

a[1:n]的最大字段和为∑ak，且1<=i<=n/2,n/2+1<=j<=n。

可用递归方法求得情形1、2。对于情形3,可以看出a[n/2]与a[n/2+1]在最优子序列中。因此可以在a[1:n/2]中计算出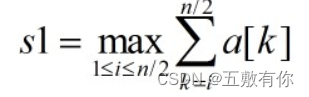

，并在a[n/2+1:n]中计算出 。则s1+s2即为出现情形3时的最优值。

????????

????????分治法采用递归的方式将问题划分成更小的子问题，分别求解子问题的最大子段和，然后合并得到整体的最大子段和。这种方法的时间复杂度为O(n log n)，适用于中等规模的数据集。它的优势在于对于更大规模的问题，其效率相对较高。

动态规化：

D[i]表示从i开始的最大字段和。（但我们不是从前往后找字段结束位置）

根据递推公式，我们可知要想求得D[i],就必须知道D[i+1],所以我们从前往后计算。

如下图：以i=12开始的子段和D[12]=X[12]=-1，该子段结束位置Rec[12]=i=12；

当i=11时，D[11+1]<0,所以D[11]=X[11]=7,Rec[i]=i=11;

当i=10时，D[10+1]>0,所以D[10]=X[10]+D[11]=3+7,Rec=i+1=11;

…
一直到i，我们就找完了所有子段和，接着在子段和中找最大的。

????????动态规划采用自底向上的方式，通过迭代计算子问题的最优解，并将结果保存起来，避免了重复计算。这种方法的时间复杂度为O(n)，适用于大规模数据集。它的优势在于具有更好的时间效率，但相对于分治法，实现稍显复杂。

实验分析

暴力破解

源码：

//暴力破解

int sum1(int arr[],int len) {

??? int sum=0;

??? for (int i = 0; i < len; i++) {

???????? int this_sum = 0;

???????? for (int j = i; j < len; j++) {

???????????? this_sum += arr[j];

???????????? if (this_sum > sum) {

????????????????? sum = this_sum;

???????????? }

???????? }

??? }

??? return sum;

}

分治法：

//分治法

int maxSubSum(int a[], int left, int right) {



??? int sum = 0;

??? if (left == right) {

???????? sum = a[left] > 0 ? a[left] : 0;

??? }

??? else {



???????? int center = (left + right) / 2;

???????? int leftSum = maxSubSum(a, left, center);

???????? int rightSum = maxSubSum(a, center + 1, right);



???????? int s1 = 0;

???????? int lefts = 0;

???????? for (int i = center; i >= left; i--) {



???????????? lefts += a[i];

???????????? if (lefts > s1) s1 = lefts;

???????? }



???????? int s2 = 0;

???????? int rights = 0;

???????? for (int i = center + 1; i < right; i++) {



???????????? rights += a[i];

???????????? if (rights > s2)? s2 = rights;

???????? }

???????? sum = s1 + s2;

???????? if (sum < leftSum) sum = leftSum;

???????? if (sum < rightSum) sum = rightSum;

??? }

??? return sum;

}



int maxSum(int a[], int n) {

??? return maxSubSum(a, 0, n - 1);

}

动态规划：

//动态规划

int sum2(int arr[],int len)

{

??? int sum=0;

??? int b=0;

??? int left=0;

??? int right=0;

??? for (int i = 0; i < len; i++) {

???????? if (b > 0) {

???????????? b += arr[i];

???????????? right = i;

???????? }

???????? else {

???????????? b = arr[i];



???????? }



???????? if (sum < b) {

???????????? sum = b;



???????? }

??? }

???

??? return sum;



}

实验分析:

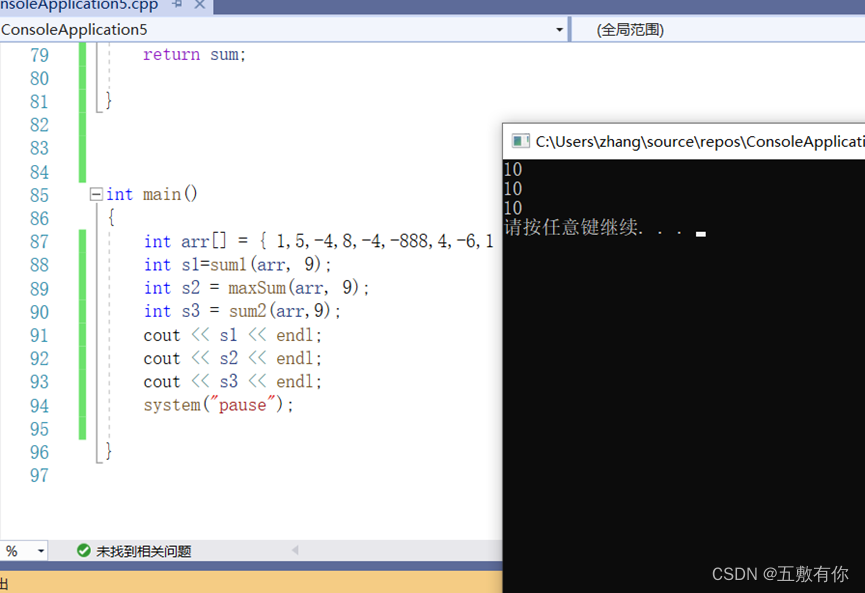
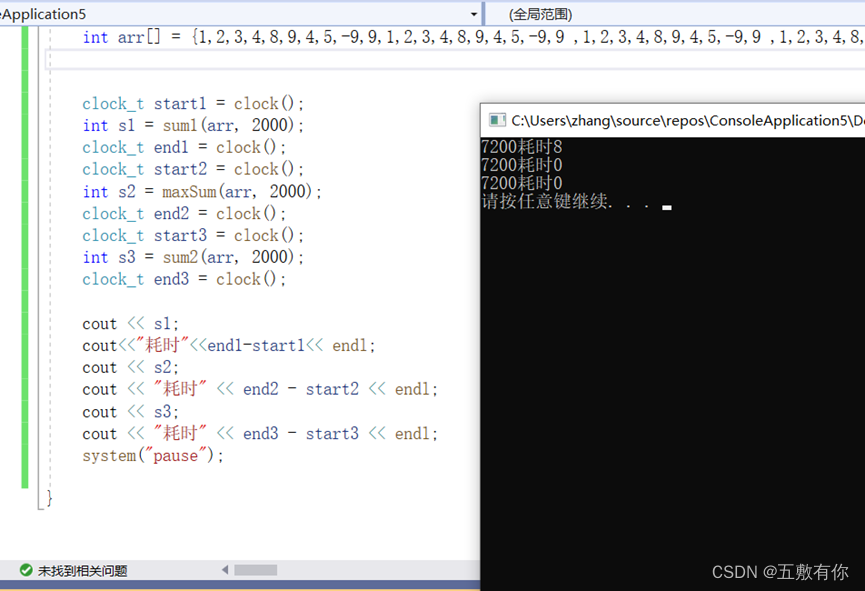
测试了2000个数据，除了暴力破解比较慢用了8ms，其他的都不足1ms。