Frequency-domain MLPs are More EffectiveLearners in Time Series Forecasting

本论文来自于?37th Conference on Neural Information Processing Systems (NeurIPS 2023)
Abstract
? ? ? ? ? ? ?时间序列预测在金融、交通、能源、医疗等不同行业中发挥着关键作用。虽然现有文献设计了许多基于 RNN、GNN 或 Transformer 的复杂架构(注意力机制的计算太占用资源,速度慢),但提出了另一种基于多层感知器(MLP)的方法,其结构简单、复杂度低且性能优越。然而,大多数基于MLP的预测方法都存在点式映射和信息瓶颈,这在很大程度上阻碍了预测性能。为了克服这个问题,我们探索了在频域中应用 MLP 进行时间序列预测的新方向。
点式映射(Pointwise Mapping)
定义:指的是在神经网络中,将输入的每个元素映射到输出中的一个相应元素。具体而言,这是指网络中的某些层(通常是全连接层或1x1卷积层)执行的逐元素操作,而不是跨多个元素的操作。
问题:点式映射可能导致模型在学习时过于注重输入中的每个细节,而缺乏对整体结构和上下文的把握。这可能使模型更容易受到噪声的干扰,丧失对输入数据中潜在结构的抽象能力。
信息瓶颈(Information Bottleneck)
定义:信息瓶颈理论认为,在学习过程中,模型应该保留对输入数据的关键信息,而丢弃冗余信息。这可以通过对网络的某些部分引入约束来实现,以限制信息的传递或压缩信息表示。
问题:当信息瓶颈设置得太紧,模型可能会失去对有用信息的捕捉,导致欠拟合。反之,如果信息瓶颈不足,模型可能过度关注冗余信息,导致过拟合。
本文研究了频域 MLP 的学习模式,发现了它们有利于预测的两个固有特征:
(i)全局视图:频谱使 MLP 拥有完整的信号视图并更容易学习全局依赖性,以及
(ii)能量压缩:频域mlp集中在频率成分的较小关键部分,信号能量紧凑。
然后,我们提出了 FreTS,这是一种基于频域 MLP 的简单而有效的架构,用于时间序列预测。
FreTS主要涉及两个阶段:
(i)域转换,将时域信号转换为频域复数;
(ii) 频率学习,执行我们重新设计的 MLP,以学习频率分量的实部和虚部。
上述在系列间和系列内尺度上运行的阶段进一步有助于通道方面和时间方面的依赖性学习。对 13 个现实世界基准(包括 7 个短期预测基准和 6 个长期预测基准)进行的广泛实验证明了我们相对于最先进方法的一贯优势。
1 Introduction
??时间序列预测在各种现实行业中发挥着关键作用,例如气候条件估计[1,2,3]、交通状态预测[4,5,6]、经济分析[7,8]等早期,已经提出了许多传统的统计预测方法,例如指数平滑[9]和自回归移动平均(ARMA)[10]。近年来,深度学习的新兴发展催生了许多深度预测模型,包括基于循环神经网络的方法(例如 DeepAR [11]、LSTNet [12])、基于卷积神经网络的方法(例如 TCN [13]、 SCINet [14])、基于 Transformer 的方法(例如 Informer [15]、Autoformer [16])和基于图神经网络的方法(例如 MTGNN [17]、StemGNN [18]、AGCRN [19]), ETC。
??虽然这些深度模型在某些场景中取得了有希望的预测性能,但它们复杂的网络架构通常会在训练或推理阶段带来昂贵的计算负担。此外,这些模型的鲁棒性很容易受到大量参数的影响,特别是当可用的训练数据有限时[15, 20]。因此,最近出现了基于多层感知器(MLP)的方法,其结构简单,复杂度低,预测性能优越,例如N-BEATS [21],LightTS [22],DLinear [23]等。然而,这些基于 MLP 的方法依赖于逐点映射来捕获时间映射,这无法处理时间序列的全局依赖性。此外,它们会受到时间序列不稳定和冗余局部动量的信息瓶颈的影响,这在很大程度上阻碍了它们的时间序列预测性能。
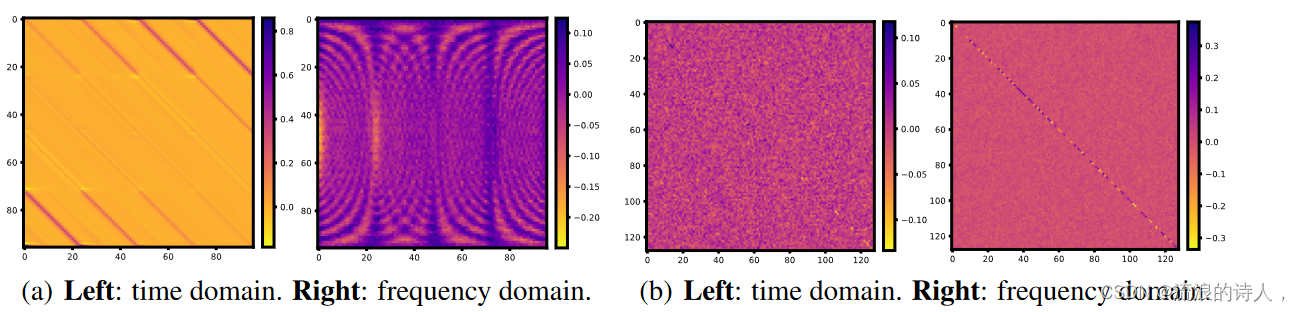
?图 1:时域和频域中 MLP 学习模式的可视化(参见附录 B.4)。
(a) 全局视图:在频域中学习到的模式比时域中表现出更明显的全局周期性模式;
(b)能量压缩:频域学习可以识别比时域更清晰的对角依赖性和关键模式。
??为了克服上述问题,我们探索了在频域中应用 MLP 进行时间序列预测的新方向。我们研究了频域 MLP 在预测中的学习模式,并发现了它们的两个关键优势:
(i)全局视图:对从级数变换获得的频谱分量进行操作,频域 MLP 可以捕获更完整的信号视图,从而使其成为可能。更容易学习全局空间/时间依赖性。
(ii)能量压缩:频域MLP集中于信号能量紧凑的频率分量的较小关键部分,因此可以在滤除噪声影响的同时保留更清晰的模式。通过实验,我们观察到频域 MLP 比图 1(a)中的时域 MLP 捕获了更明显的全局周期模式,这凸显了它们识别全局信号的??能力。此外,从图 1(b) 中,我们很容易注意到,与时域 MLP 学习到的更分散的依赖关系相比,频域 MLP 学习到的权重中存在更清晰的对角依赖关系。这说明了频域 MLP 在处理复杂和噪声信息时识别最重要特征和关键模式的巨大潜力。
??为了充分利用这些优势,我们提出了 FreTS,这是一种用于时间序列预测的简单而有效的频域 MLP 架构。 FreTS的核心思想是学习频域中的时间序列预测映射。具体来说,
FreTS主要涉及两个阶段:
(i)域转换:原始时域序列信号首先在离散傅里叶变换(DFT)[24]之上变换为频域频谱,其中频谱由几个复数组成:频率分量,包括实系数和虚系数。
(ii)频率学习:给定实部/虚部系数,我们通过分别考虑实部映射和虚部映射来重新设计最初用于复数的频域MLP。然后,将两个不同 MLP 学习到的输出的相应实部/虚部进行堆叠,以便从频率分量恢复到最终预测。此外,FreTS 在系列间和系列内尺度上执行上述两个阶段,这进一步有助于频域中的通道和时间依赖性,以获得更好的预测性能。我们在不同设置下对 13 个基准进行了广泛的实验,涵盖 7 个短期预测基准和 6 个长期预测基准,这证明了我们与最先进的方法相比始终具有的优越性。
2 Related Work
Forecasting in the Time Domain
??传统上,已经提出了用于时域预测的统计方法,包括(ARMA)[10]、VAR[25]和ARIMA[26]。最近深度学习基于的方法由于其提取非线性和复杂相关性的能力而被广泛应用于时间序列预测[27, 28]。这些方法已经学习了 RNN(例如,deepAR [11]、LSTNet [12])和 CNN(例如,TCN [13]、SCINet [14])在时域中的依赖性。此外,基于 GNN 的模型由于能够很好地建模时域变量之间的序列依赖关系,因此具有良好的预测性能,例如 TAMP-S2GCNets [5]、AGCRN [19]、MTGNN [17] ,和 GraphWaveNet [29]。此外,基于 Transformer 的预测方法由于其对时域远程依赖建模能力的关注机制而被引入,例如 Reformer [20] 和 Informer [15]。
Forecasting in the Frequency Domain
??最近的几种时间序列预测方法已经提取了频域知识来进行预测[30]。具体来说,SFM[31]通过离散傅里叶变换(DFT)将LSTM的隐藏状态分解为频率。 StemGNN [18] 基于图傅立叶变换(GFT)执行图卷积,并基于离散傅立叶变换计算级数相关性。 Autoformer [16] 通过提出用快速傅立叶变换(FFT)实现的自相关机制来取代自注意力。 FEDformer[32]提出了一种基于DFT的频率增强注意力,通过查询和密钥的频谱获得注意力权重,并计算频域的加权和。 CoST [33] 使用 DFT 将中间特征映射到频域,以实现表示中的交互。 FiLM [34] 利用傅里叶分析来保留历史信息并消除噪声信号。与这些利用频率技术改进 Transformer 和 GNN 等原始架构的努力不同,在本文中,我们提出了一种新的频率学习架构,可以学习频域中的通道依赖性和时间依赖性。
MLP-based Forecasting Models
??一些研究探索了基于 MLP 的网络在时间序列预测中的使用。 N-BEATS [21] 利用堆叠的 MLP 层和双残差学习来处理输入数据以迭代地预测未来。 DEPTS [35] 应用傅立叶变换来提取周期和 MLP,以实现单变量预测的周期性依赖性。 LightTS [22] 使用轻量级面向采样的 MLP 结构来降低复杂性和计算时间,同时保持准确性。 N-HiTS [36] 将多速率输入采样和分层插值与 MLP 结合起来进行单变量预测。 LTSF-Linear [37]提出了一组极其简单的单层线性模型来学习输入和输出序列之间的时间关系。这些研究证明了基于 MLP 的网络在时间序列预测任务中的有效性,并启发了本文中频域 MLP 的开发。
3 FreTS
??在本节中,我们将详细阐述我们提出的新方法 FreTS,该方法基于我们在频域中重新设计的用于时间序列预测的 MLP。首先,我们在3.1节中介绍了FreTS的详细频率学习架构,其中主要包括具有域转换的两倍频率学习器。然后,我们在 3.2 节中详细介绍了上述频率学习器采用的重新设计的频域 MLP。此外,我们还从理论上分析了它们的全球视野和能量压缩的优越性,如第一节所述。
Problem Definition
??设 [X1, X2, ···, XT ] ∈ RN×T 表示具有 N 个序列和 T 个时间戳的定期采样的多元时间序列数据集,其中 Xt ∈ RN 表示 N 个不同序列在时间戳处的多元值t。我们将时间戳 t 处长度为 L 的时间序列回溯窗口视为模型输入,即 Xt = [Xt?L+1, Xt?L+2, · · · , Xt] ∈ RN×L;此外,我们将时间戳 t 处长度为 τ 的水平窗口视为预测目标,表示为 Yt = [Xt+1, Xt+2, · · · , Xt+τ ] ∈ RN×τ 。那么时间序列预测公式是使用历史观测值 Xt 来预测未来值 ? Yt,并且由 θ 参数化的典型预测模型 fθ 是通过 ? Yt = fθ(Xt) 产生预测结果
3.1 Frequency Learning Architecture
??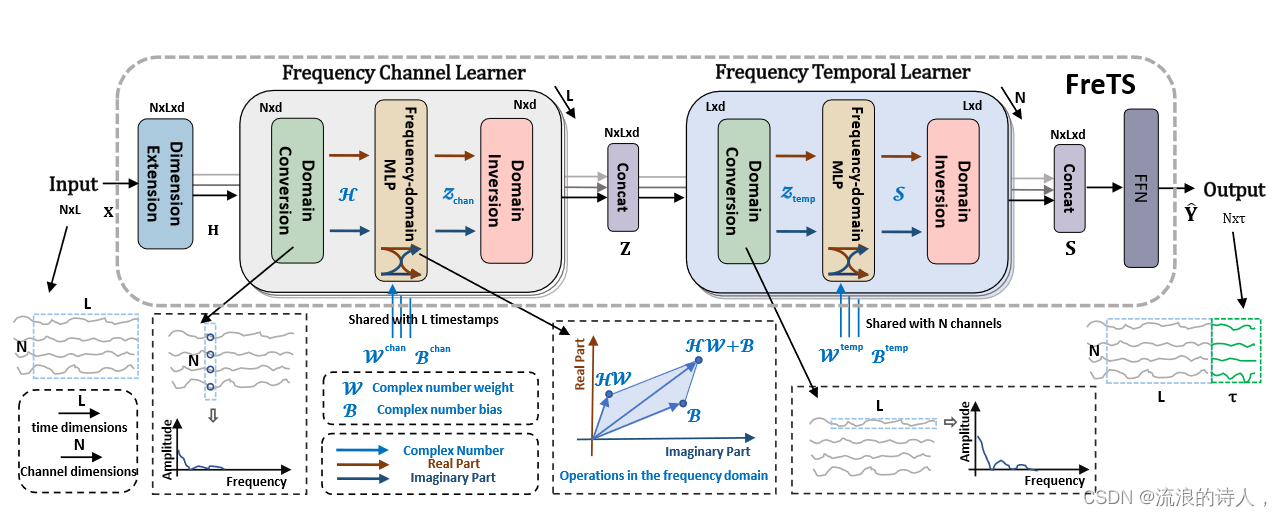
?图 2:FreTS 的框架概述:频率通道学习器侧重于使用在通道维度上操作的频域 MLP 来建模系列间依赖关系;频率时间学习器是通过在时间维度上执行频域 MLP 来捕获时间依赖性。
? ? FreTS的频率学习架构如图2所示,主要涉及域转换/反转阶段、频域MLP以及相应的两个学习器,即频率通道学习器和频率时间学习器。此外,在提供给学习者之前,我们在模型输入上具体应用了维度扩展块来增强模型能力。具体来说,输入回溯窗口 Xt ∈ RN×L 乘以可学习的受词嵌入[38]的启发,权向量 φd ∈ R1×d 以获得更具表现力的隐藏表示 Ht ∈ RN×L×d,产生 Ht = Xt × φd 以带来更多语义信息。
Domain Conversion/Inversion
使用傅立叶变换可以将时间序列信号分解为其组成频率。这对于时间序列分析特别有利,因为它有利于识别数据中的周期性或趋势模式,这在预测任务中通常很重要。如图 1(a) 所示,频谱学习有助于捕获更多的周期性模式。鉴于此,我们通过以下方式将输入H转换为频域H:

?其中我们将频率 f 作为积分变量。事实上,频谱表示为 H 中具有不同频率和幅度的余弦波和正弦波的组合,从而推断出时间序列信号中不同的周期特性。因此,检查频谱可以更好地辨别时间序列中的突出频率和周期性模式。在以下各节中,为了简洁起见,我们使用 DomainConversion 代表方程(1),使用 DomainInversion 代表方程(2)。
Frequency Channel Learner
? ?考虑时间序列预测的通道依赖性很重要,因为它允许模型捕获不同变量之间的相互作用和相关性,从而实现更准确的预测。频道学习器能够实现不同频道之间的通信;它通过在 L 个时间戳之间共享相同的权重来对每个时间戳进行操作,以学习通道依赖性。具体地,频道学习器将Ht ∈ RN×L×d作为输入。给定第 l 个时间戳 H:,(l) t ∈ RN×d,我们通过以下方式执行频率通道学习器:

?
?Frequency Temporal Learner
? ?频率时间学习器旨在学习频域中的时间模式;此外,它是基于在每个通道上进行的频域 MLP 构建的,并且在 N 个通道之间共享权重。具体来说,它以频率通道学习器输出 Zt ∈ RN×L×d 作为输入,对于第 n 个通道 Z(n): t ∈ RL×d,我们通过以下方式应用频率时间学习器:

?3.2 Frequency-domain MLPs
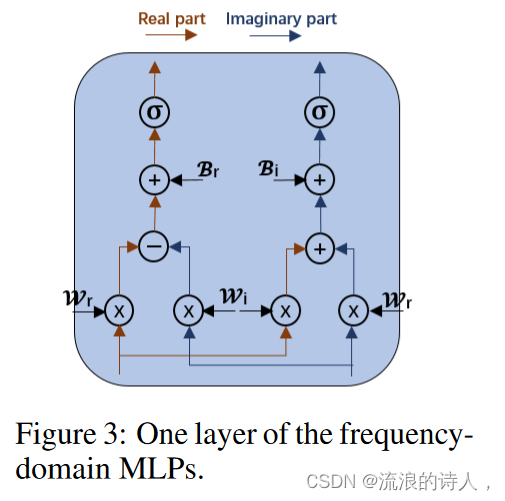
? ?如图 3 所示,我们在 FreTS 中阐述了新颖的频域 MLP,这些 MLP 针对复数频率分量进行了重新设计,以便通过全局视图和能量压缩有效捕获时间序列关键模式,如第 1 节中所述。
定义 1(频域 MLP)。形式上,对于复数输入 H ∈ Cm×d,给定复数权重矩阵 W ∈ Cd×d 和复数偏差 B ∈ Cd,则频域 MLP 可以表示为:
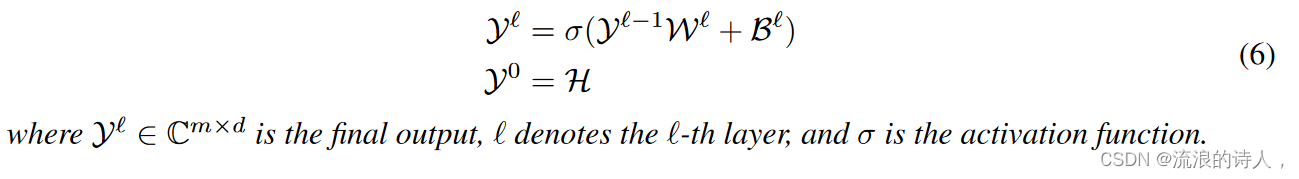 定理1.假设H是原始时间序列的表示,H是频谱的相应频率分量,则时间序列在时域中的能量等于其在频域中表示的能量。正式地,我们可以用上面的符号来表达:?
定理1.假设H是原始时间序列的表示,H是频谱的相应频率分量,则时间序列在时域中的能量等于其在频域中表示的能量。正式地,我们可以用上面的符号来表达:?
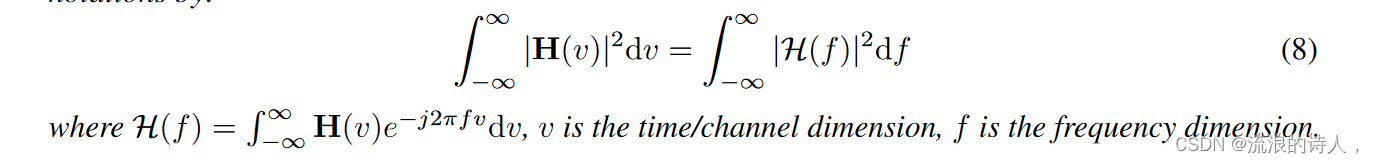
?我们将证明包含在附录 D.1 中。该定理意味着,如果时间序列的大部分能量集中在少数频率分量中,则仅使用这些分量就可以准确地表示时间序列。因此,丢弃其他信号不会显着影响信号的能量。如图1(b)所示,在频域中,能量集中在频率分量的较小部分上,因此频谱中的学习可以有利于保留更清晰的模式。
定理2.给定时间序列输入H及其对应的频域转换H,频域MLP对H的操作可以表示为时域中对H的全局卷积。这可以由下式给出:
?
?
4 Experiments
??为了评估 FreTS 的性能,我们对 13 个现实世界时间序列基准进行了广泛的实验,涵盖短期预测和长期预测设置,以与相应的最先进方法进行比较。
数据集? ? 我们的实证结果是在各个领域的数据集上进行的,包括交通、能源、网络、交通、心电图和医疗保健等。具体来说,对于短期预测的任务,我们采用 Solar 2、Wiki [39]、Traffic [39]、Electricity 3、ECG [18]、METR-LA [40] 和 COVID-19 [5] 数据集,遵循之前的预测文献 [18]。对于长期预测任务,我们采用天气[16]、交易所[12]、交通[16]、电力[16]和ETT数据集[15],继之前的长期时间序列预测工作[15、16、32、 41]。我们预处理[18,15,16]之后的所有数据集,并使用最小-最大归一化对其进行归一化。我们按 7:2:1 的比例将数据集分为训练集、验证集和测试集,但 COVID-19 数据集的比例为 6:2:2。更多数据集详细信息参见附录 B.1。
Baselines??我们将 FreTS 与短期和长期预测的代表性和最先进的模型进行比较,以评估其有效性。对于短期预测,我们将 FreTS 与 VAR [25]、SFM [31]、LSTNet [12]、TCN [13]、GraphWaveNet [29]、DeepGLO [39]、StemGNN [18]、MTGNN [17] 进行比较,和 AGCRN [19] 进行比较。我们还包括 TAMP-S2GCNets [5]、DCRNN [40] 和 STGCN [42],它们需要预定义的图结构,以进行比较。对于长期预测,我们包括 Informer [15]、Autoformer [16]、Reformer [20]、FEDformer [32]、LTSF-Linear [37] 和更新的 PatchTST [41] 进行比较。有关基线的更多详细信息可以在附录 B.2 中找到。
Implementation Details?
我们的模型使用 Pytorch 1.8 [43] 实现,所有实验均在单个 NVIDIA RTX 3080 10GB GPU 上进行。我们以MSE(均方误差)作为损失函数,并报告MAE(平均绝对误差)和RMSE(均方根误差)结果作为评估指标。有关其他实施细节,请参阅附录 B.3。
4.1 Main Results
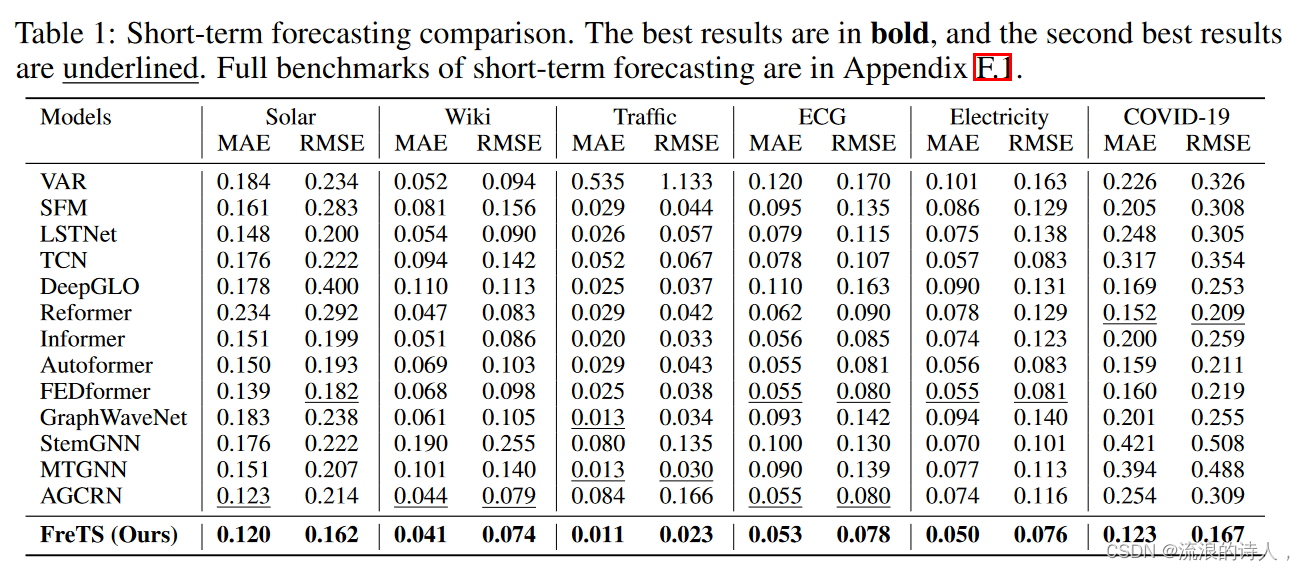
?Short-Term Time Series Forecasting
?表 1 显示了我们的 FreTS 与 6 个数据集上的 13 个基线相比的预测准确性,其中输入长度为 12,预测长度为 12。最好的结果以粗体突出显示,次好的结果用下划线表示。从表中我们观察到,FreTS 在所有数据集上的 MAE 和 RMSE 方面均优于所有基线,平均而言,它在 MAE 上提高了 9.4%,在 RMSE 上提高了 11.6%。我们将此归功于 FreTS 显式地对通道和时间依赖性进行建模,并且它在频域中灵活地统一了通道和时间建模,可以通过全局视图和能量压缩有效地捕获关键模式。我们在附录 F.1 中进一步报告了不同数据集(包括 METR-LA 数据集)上不同步骤下的短期预测的完整基准。
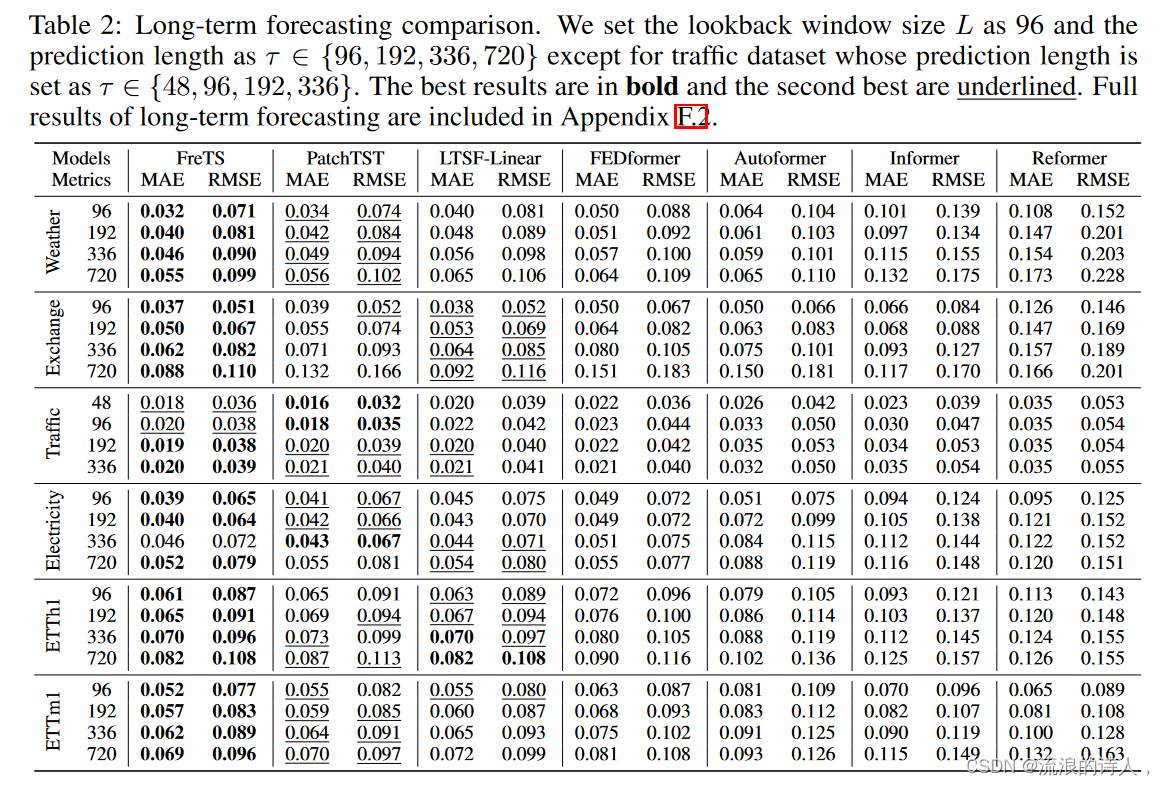
Long-term Time Series Forecasting
??表 2 显示了 FreTS 的长期预测结果,与具有不同预测长度的六个基准上的六个代表性基线相比。对于流量数据集,我们选择 48 作为回溯窗口大小 L,预测长度为 τ ∈ {48, 96, 192, 336}。对于其他数据集,输入回溯窗口长度设置为 96,预测长度设置为 τ ∈ {96, 192, 336, 720}。结果表明 FreTS 在所有数据集上均优于所有基线。定量来看,与基于 Transformer 的模型的最佳结果相比,FreTS 在 MAE 和 RMSE 上平均下降了 20% 以上。与最近的 LSTF-Linear [37] 和 SOTA PathchTST [41] 相比,FreTS 总体上仍然可以胜过它们。此外,我们在附录 F.2 中提供了 FreTS 与其他基线的进一步比较,并报告了不同回溯窗口大小下的性能。结合表1和表2,我们可以得出结论,FreTS在短期和长期预测任务中都取得了有竞争力的表现。
4.2 Model Analysis
Frequency Channel and Temporal Learners
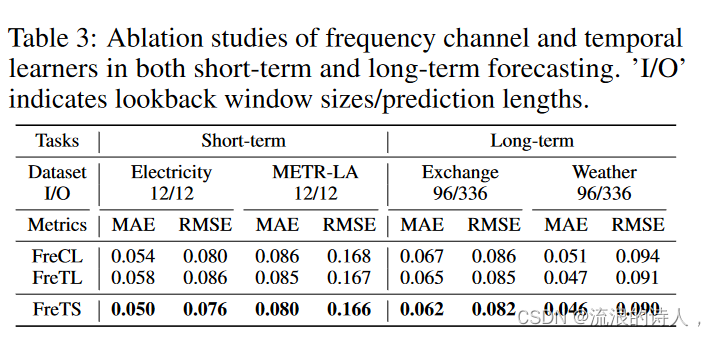
? ?我们分析了表 3 中短期和长期实验设置中频道和时间学习者的影响。我们考虑两种变体:FreCL:我们从 FreTS 中删除频率时间学习器,以及 FreTL:我们从 FreTS 中删除频率通道学习器。从比较中,我们观察到频道学习器在短期预测中发挥着更重要的作用。在长期预测中,我们注意到频率时间学习器比频率通道学习器更有效。在附录 E.1 中,我们还在其他数据集上进行了实验并报告了性能。有趣的是,我们发现通道学习器在某些长期预测情况下会导致性能更差。一个可能的解释是,渠道独立策略[41]为预测带来了更多好处。
FreMLP vs. MLP
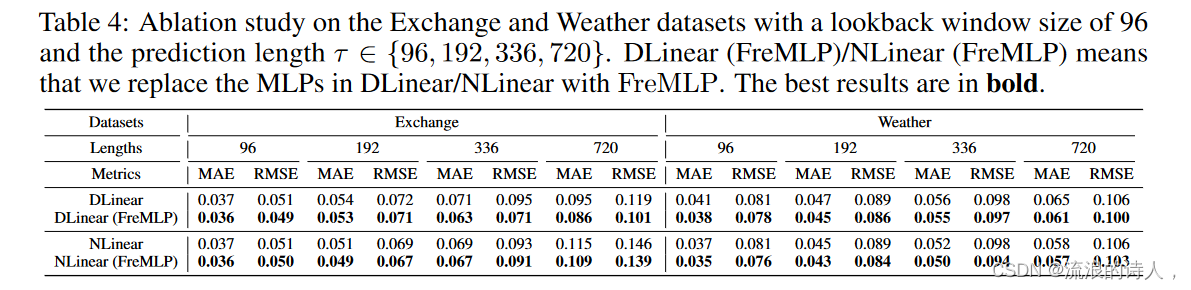
??我们进一步研究 FreMLP 在时间序列预测中的有效性。我们使用 FreMLP 替换现有基于 SOTA MLP 的模型(即 DLinear 和 NLinear [37])中的原始 MLP 组件,并在相同的实验设置下将它们的性能与原始的 DLinear 和 NLinear 进行比较。实验结果如表 4 所示。从表中,我们很容易观察到,对于任何预测长度,用我们的 FreMLP 替换相应的 MLP 组件后,DLinear 和 NLinear 模型的性能都得到了提高。从数量上来说,将 FreMLP 纳入 DLinear 模型后,Exchange 数据集上的 MAE 平均提高了 6.4%,RMSE 平均提高了 11.4%,而 Weather 数据集上的 MAE 平均提高了 4.9%,RMSE 平均提高了 3.5%。根据表 4,两个数据集上的 NLinear 也取得了类似的改进。这些结果再次证实了 FreMLP 相对于 MLP 的有效性,我们在附录 B.5 中包含了更多实现细节和分析。
5 Conclusion Remarks
??在本文中,我们探索了一个新的方向,并做出了将频域 MLP 用于时间序列预测的新尝试。我们在频域中重新设计了 MLP,可以通过全局视图和能量压缩有效捕获时间序列的基本模式。然后,我们通过一个简单而有效的架构 FreTS 验证了该设计,该架构基于频域 MLP 构建,用于时间序列预测。我们对七个短期预测基准和六个长期预测基准的综合实证实验验证了我们提出的方法的优越性。简单的 MLP 具有多种优势,为现代深度学习奠定了基础,具有获得令人满意的高效率性能的巨大潜力。我们希望这项工作能够促进 MLP 在时间序列建模方面的更多未来研究。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!