16.蒙特卡洛积分、路径追踪000000000

1.前置知识：概率论

• 随机变量：可能取很多值的数
• 随机变量的分布：取某个值有个大概率，另外的小概率
• 举例：骰子可能的值是1-6，取到每一个的概率是相等的

• 概率：大于0的，且所有可能的和为1

• 期望（不断取随机变量，取平均）

• 连续情况下的变量和它的分布

pdf：概率密度函数

随机变量函数

2.Monte Carlo Integration—蒙特卡洛积分

蒙特卡洛积分的理解：用一个随机的采样的方法。随意取一个点，对应f(x)为高，a→b为宽，（假设为长方形）来近似线下的面积，重复多次采样，最后平均起来长方形的面积。

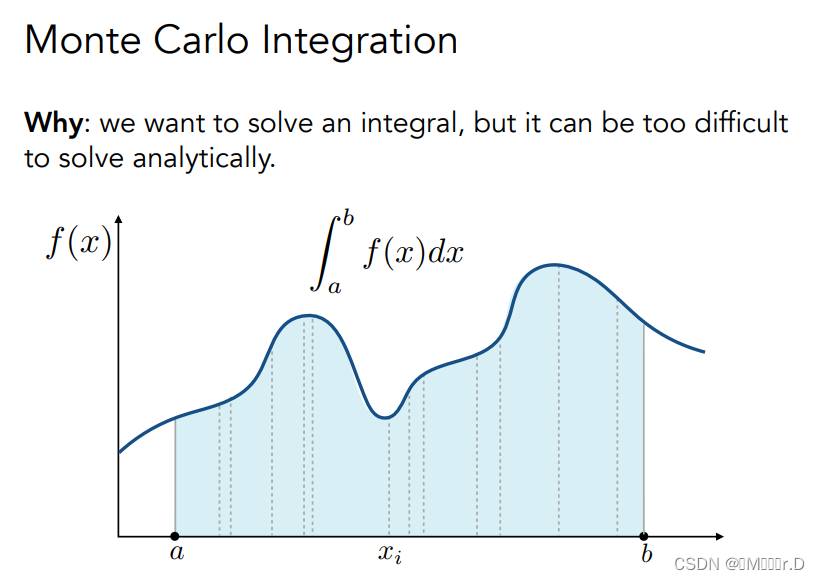
蒙特卡洛积分的定义：

如果在a-b之间均匀采样的话，也就是说每一个x取到的概率都是相同的。那么就可以得到概率密度函数就是1/a-b。其实这也就是近似的长方形的宽度。

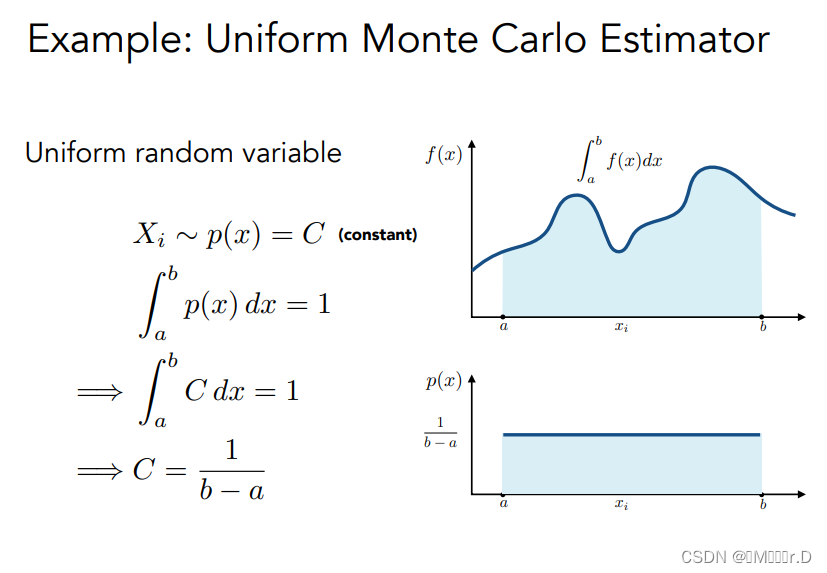
将这个结果带入式子里的结果就是这样：

当然均匀采样的是特殊情况，下面的式子适用于所有的情况，p（xi）就可以理解成近似长方形的宽度

注意：

①采样越多，越准确。

为什么b-a没有了 ： p（x）永远是1/b-a→拿到外边→消掉了（不用关心积分域，pdf中已经体现出）

②定义在x域上，采样也要在x域上（定义和采样要在一个域）

3.Path Tracing-路径追踪?

1.Whitted-style光线追踪的问题

Glossy材质的错误表现

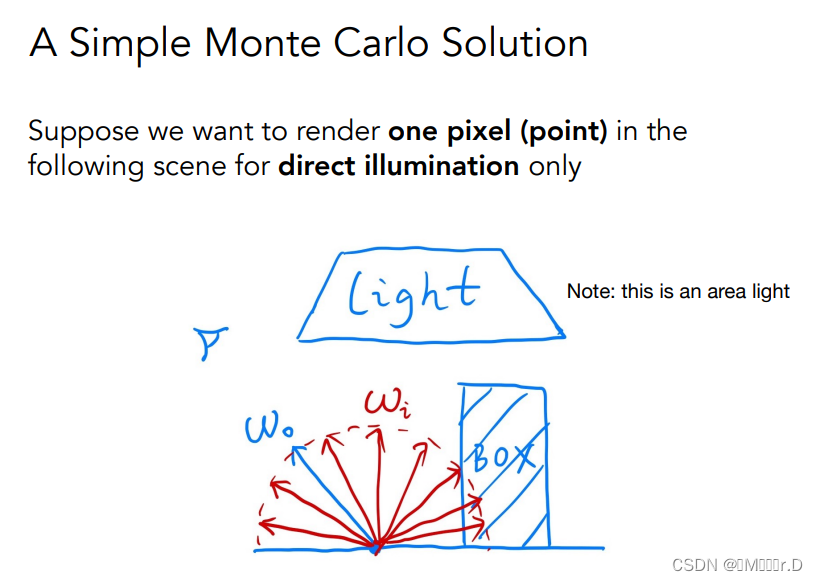
对于Whitted-Style光线追踪，假象了发生的反射都是镜面反射，但是事实上在有些时候并不是这样，如下图右边的Glossy反射，它看上去并不光滑，而是相对模糊，也就说明它反射的时候是对一小片区域进行反射，而不是完美的一条直线。

漫反射材质之间缺少反射

之前在做Whitted-Style光线追踪的过程中，发出eye ray之后打到透明材质折射，反射，但是当打到漫反射材质的时候却没有继续进行下去，这显然是不对的，因为光线在打到漫反射材质的时候还会继续在场景中弹射，上图揭示了这一规律。(左:无全局光照/右:有全局光照)

2.用蒙特卡洛积分来求解渲染方程

先考虑直接光照（光源直接发出的光）并且先不考虑自发光

现在渲染方程就只有一项对半球进行积分

这里函数就是积分后面那一串，pdf就是1/2PI；因为整个球面的立体角是4PI，半球的就是2PI，并且这里使用均匀分布采样

将参数分别带入以后的结果如下，同时下面还有通过蒙特卡洛积分求解渲染方程只计算直接光照的伪码

间接光照

如果我们从摄像机发出一条光线打到上图中P点，和光源连线，那么这计算的是P点的直接光照，但是我们不能忽略Q点对P点的光照的贡献，也就是间接光照。在渲染方程中我们提到，对于一个着色点，我们所作的积分中，并不区分是直接光照还是间接光照，那么直接光照我们前面已经提到了如何求解，Q点的间接光照呢？

很简单，我们想象在P点有一个摄像机沿着Q的反射方向看向Q点，那么P点接收来自Q点的间接光照就相当于Q点接收到光源的直接光照反射后得到的结果。

于是在上面的伪码上我们可以增加一项。如下图，而这恰恰是一种递归算法。

但是这里有一个问题，就是光线在递归之后会越来越多，如果我们设置递归发出的光线是100条，那么在递归的算法下，我们每次弹射都会再反射出100条光线，而我们的弹射点又不止一个，这是一个指数级的增加，会产生指数爆炸。

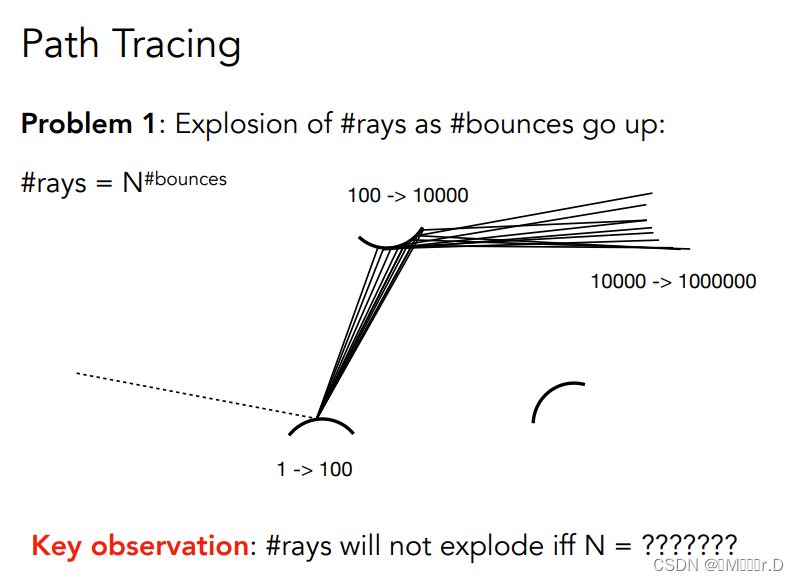
解决方法也很简单，1的多少次方都是1，所以我们不用100根光线，只用一根光线即可解决指数爆炸问题。所以修改一下伪码如下图所示。

这样就得到了一个极其简化的公式(如下面伪码所示)因为我们的采样方向变成了1个，也就是N=1。而N=1的这种方法就叫做路径追踪。而如果N≠1，这是另一种，叫做分布式光线追踪，会产生指数爆炸。

但是我们如果只发出一条光线，会产生非常多的噪点。其实我们在一个像素中会发出很多条光线，而通过这些光线在场景中的不断弹射，最终这个像素会得到这个着色点接收不同弹射点的着色结果之和。

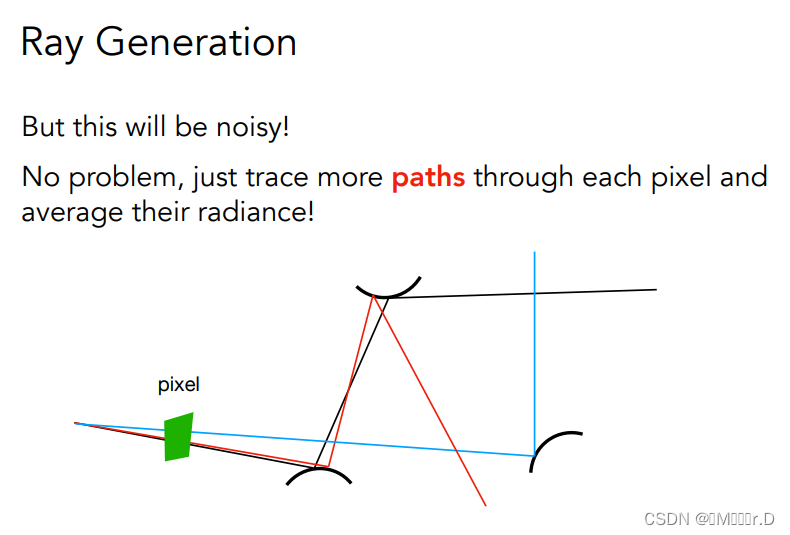
同样的可以写出伪码，如下图：在一个像素里发出N条path，也就是采样，对于每个像素的每个path发出一条光线，如果它打到了场景中的某个点p，该像素的radiance就等于不断累加的着色之和，而这里同样用到了蒙特卡洛积分方法。

但是现在仍然有问题，我们说过这个着色的算法是一个递归的算法，但是递归需要停止条件，而我们写的着色方法就是没有停止条件，它反映了光线弹射无限次，而现实中就是这样，但是这在计算机中是不能实现的，而如果我们把它限制在某一个固定的弹射次数违背了能量守恒，它损失了很多能量的计算，这也是不对的，那该怎么办呢？

俄罗斯轮盘赌，简称RR，假如一把左轮枪里面装2发子弹，(弹匣容量6)，然后朝自己开枪，那么活下来的概率就是4/6。那么这和光线弹射有什么关系呢？

对于每一条发射出的path，到达着色点的时候，我们提前设置一个概率P，让它以P的概率决定它继不继续进行弹射，如果弹射了，那么最终计算的积分结果我们取Lo/P，否则取0。这么做的原因是当我们取期望的时候，我们会发现我们的期望是Lo，也就是正确的。

最后根据这个就可以得到下面的伪代码

但是此时得到的图像效果质量取决于我们的SPP(samples per pixel)，也就是每个像素发出的path数量，也就是采样率。也就说明，我们的算法并不是那么高效。

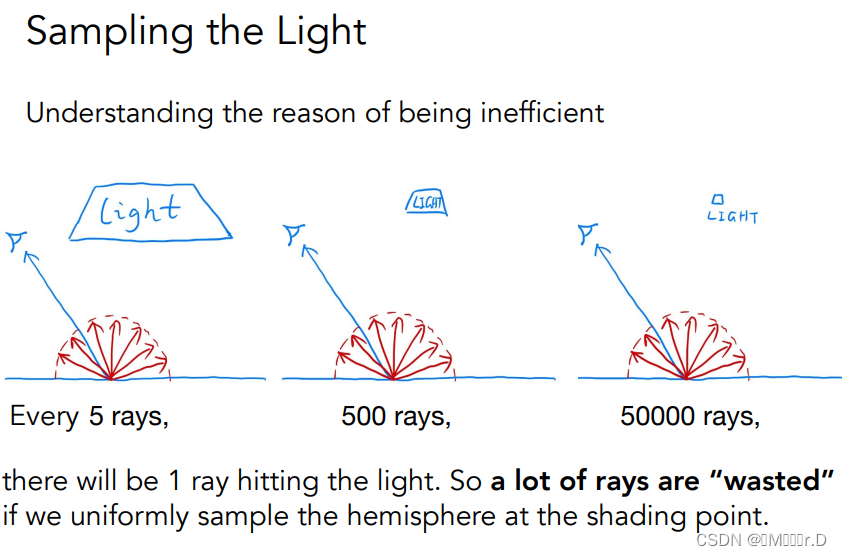
对于每一个着色点，我们是均匀的朝着四面八方采样的，也就是说，我们的光线能否能打到光源完全取决于运气，如果光源小，那么我们就会浪费许多光线，如最右图，我们平均每发射50000条光线才能打中一次光源。也就是说我们需要换一种采样方式。而且我们之前在说蒙特卡洛方法的时候特意提到了，采样分布函数不一定非要用均匀分布函数。

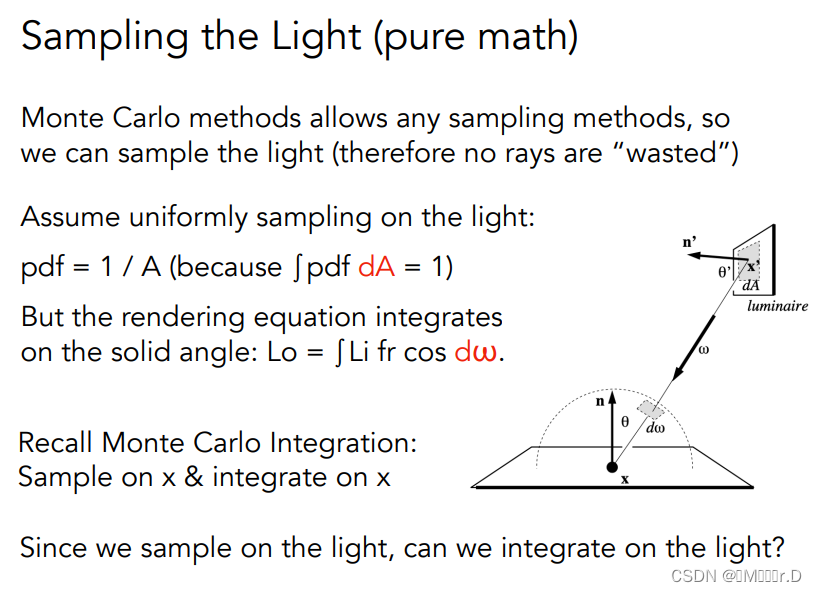
3.改写渲染方程：直接对光源采样

上面说过如果光源小的情况就算发出几万条光线也不一定能打到光线，为了解决这个问题，可以考虑在光源上进行均匀采样。

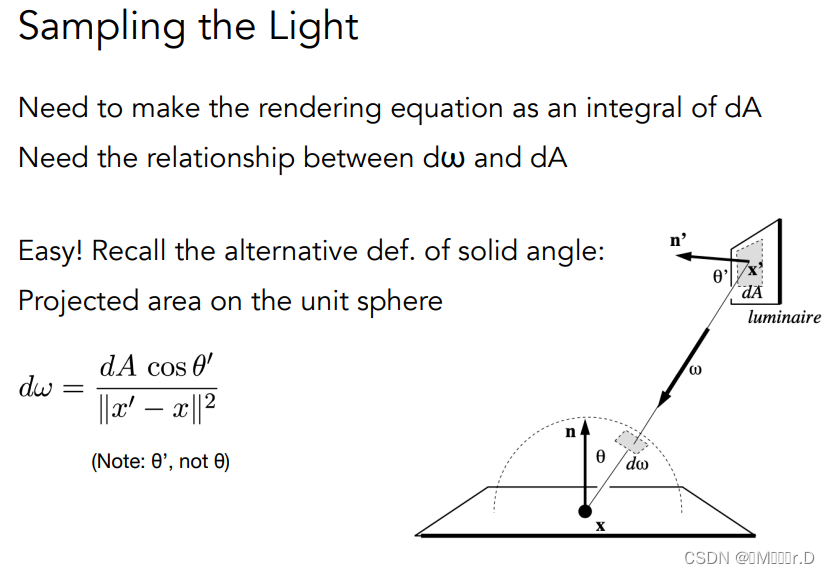
但是之前说过蒙特卡洛积分的采样和积分的对象应该是一样的，因此要把对立体角的积分改写成对光源面积投影到半球面积的积分。也就是从对dω积分改为对dA积分，我们只需要知道dω和dA的关系然后替换即可。

怎么替换？我们想想立体角的定义，面积除以距离平方，那我们只需要把dA这块面积投影到球面上然后除以着色点x和光源处点x'距离的平方即可，面积投影可以用cosθ'求得。而采样分布函数p(X)就是1/A，因为我们在光源上进行均匀的采样。这样一来我们就把渲染方程改为了对光源的积分。

而由此，我们就可以把任何一个着色点接收光的贡献拆成两部分，一部分是光源的直接光照对该着色点的贡献，另一部分则是间接光照的贡献。而光源直接的贡献经过我们改写的渲染方程积分之后可以直接得出，而且只涉及到一次弹射，所以光源这部分不需要用俄罗斯轮盘赌。

接着就可以得到下面的伪代码

但是还有一个问题，我们并没有判断着色点和光源之间是否有遮挡。

从p与光源的连线向光源发出一条光线，如果能到达光源，则说明该点与光源之间没有遮挡，也就是可以计算光源对该着色点的直接贡献，否则只计算间接光照，也就是除光源外的其它贡献。而到此，路径追踪的一整套流程就都完成了，而它基本上是100%正确的。

点光源怎么办：对于路径追踪很难做，建议最好把点光源换成一个很小的面光源

一些不那么重要的事情：

①Path Tracing很难实现

②还是入门吗？？ 算进阶

③Path Tracing 几乎100%正确

4.Ray Tracing：过去的光追VS现在的概念

1.以前

基本都是指Whitted-style 的光线追踪

2.Now（老师自己的定义）

所有光线传播方法的大集合

• (Unidirectional & bidirectional) path tracing
• Photon mapping
• Metropolis light transport
• VCM / UPBP…

5.没有说的问题

1.如何对半球进行采样？——采样理论

2.蒙特卡洛积分所用的pdf可以是任意的PDF，什么样的PDF是最好的？——重要性采样

3.随机数的选取优劣，随机数可以均匀分布在0~1——低差异序列

4.对光源采样和对半球采样可以相结合——多重重要性采样图形学图形学｜Robust：Multiple Importance Sampling 多重重要性采样 - 知乎 (zhihu.com)

5.像素的Radiance真的只是各种path的简单平均吗？还是加权平均？—pixel reconstruction filter

6.我们最终计算的结果是Radiance，而Radiance≠Color，如何将Radiance转化成Color呢？——伽马矫正，曲线，颜色空间
?