变分法:从原理到应用
原文链接:https://zhuanlan.zhihu.com/p/653627629
前言
需了解差分、微分的区别和联系
需了解偏微分和全微分、导数和偏导数、梯度和方向梯度的联系
需了解微分、导数、梯度的关系
需了解偏微分和全微分的表示方法
变分法简介
我们在学习微积分的过程中接触到了微分的概念,它是研究函数的一个非常重要的概念,今天笔者所介绍的变分法是基于微积分的一种更加高阶的数学方法,其主要目的是求解泛函的极值,在数学和物理学等众多领域得到了广泛的应用。
本文从函数的驻点、泛函的定义、变分原理的推导和变分原理的简单应用四个方面对变分法的原理和应用作简要的介绍,以加深对读者变分法的理解。
1.函数的驻点
驻点往往是极值存在的点,在求解函数
f
(
x
)
f(x)
f(x)在定义域内的极值时,我们常会找函数的驻点。下面介绍函数的驻点是如何得到的。
对于一个三维空间域上的函数
f
(
x
)
f(x)
f(x),给定一个位移的增量
Δ
x
=
(
x
1
,
x
2
,
x
3
)
\Delta x=(x1,x2,x3)
Δx=(x1,x2,x3),根据泰勒展开可以得到:
f
(
x
+
Δ
x
)
=
f
(
x
)
+
?
f
?
x
1
Δ
x
1
+
?
f
?
x
2
Δ
x
2
+
?
f
?
x
3
Δ
x
3
+
o
(
x
)
f(x+\Delta x)=f(x)+\frac{\partial f}{\partial x_1}\Delta x_1 +\frac{\partial f}{\partial x_2}\Delta x_2 +\frac{\partial f}{\partial x_3}\Delta x_3 + o(x)
f(x+Δx)=f(x)+?x1??f?Δx1?+?x2??f?Δx2?+?x3??f?Δx3?+o(x)
因此我们可以得到:
Δ
f
=
f
(
x
+
Δ
x
)
?
f
(
x
)
=
?
f
?
x
1
Δ
x
1
+
?
f
?
x
2
Δ
x
2
+
?
f
?
x
3
Δ
x
3
+
o
(
x
)
\Delta f=f(x+\Delta x)-f(x)=\frac{\partial f}{\partial x_1}\Delta x_1 +\frac{\partial f}{\partial x_2}\Delta x_2 +\frac{\partial f}{\partial x_3}\Delta x_3 + o(x)
Δf=f(x+Δx)?f(x)=?x1??f?Δx1?+?x2??f?Δx2?+?x3??f?Δx3?+o(x)
考虑
∣
Δ
x
∣
→
0
|\Delta x|\to0
∣Δx∣→0,忽略高阶项,我们得到:
d
f
=
?
f
?
d
x
df=\nabla f \cdot dx
df=?f?dx
对于任何方向的
d
x
dx
dx,函数的一阶微分
d
f
=
0
df=0
df=0,那么只有:
?
f
=
0
\nabla f=0
?f=0
这表示函数的驻点处梯度为0。
2.泛函的定义
对于函数的定义我们已经比较了解,函数实际上就是一个数集映照到另外一个数集的对应法则。设函数
y
=
y
(
x
)
y=y(x)
y=y(x) 定义在
a
<
x
<
b
a<x<b
a<x<b 上,那么每一个定义域内的都有唯一的与之对应。 现在我们看一下下面的表达式:
F
=
∫
a
b
[
y
(
x
)
]
3
+
y
′
(
x
)
y
′
′
(
x
)
d
x
F=\int_a^b[y(x)]^3+y'(x)y''(x)dx
F=∫ab?[y(x)]3+y′(x)y′′(x)dx
毫无疑问,
F
F
F的值与
x
x
x是无关的,那么与谁有关呢?与
y
y
y这个函数有关!只要
y
y
y这个法则发生变化,它在积分区域所有的值一般都会变化,
F
F
F的值当然也会变化。所以说泛函并不是一个很复杂的概念,泛函就是函数的函数。它只是把普通函数的自变量从数换成了函数,也就是一个法则。当然我们也可以从另一个角度理解泛函,我们知道多元函数具有多个自变量,例如:
g
=
g
(
x
1
,
x
2
,
x
3
)
g=g(x_1,x_2,x_3)
g=g(x1?,x2?,x3?)
这里的
g
g
g 是一个三元函数,其中任意一个自变量变化都会引起函数值改变。不过多元函数的自变量都是有限的,而泛函可以看成是拥有无限个自变量的多元函数,函数
y
y
y 在
a
<
x
<
b
a<x<b
a<x<b 这个区间中的所有函数值构成了它的自变量集合。无论怎么理解泛函,简单的泛函都可以用以下的形式表示:
F
[
y
]
=
∫
a
b
f
(
x
,
y
,
y
′
)
d
x
F[y]=\int_a^bf(x,y,y')dx
F[y]=∫ab?f(x,y,y′)dx
这里说简单泛函是因为只涉及到一阶导数和一重积分,更复杂的泛函可能包含更高阶导数以及多重积分。
3.变分原理的推导
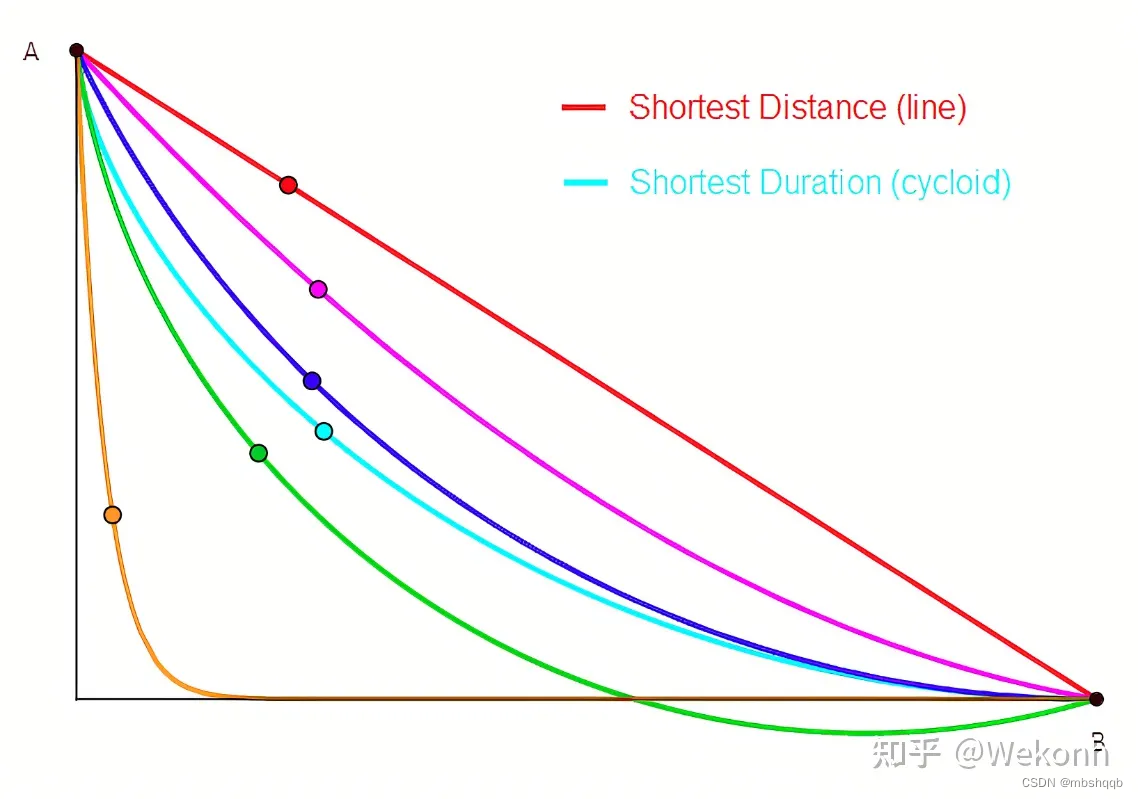
很多物理问题本质上都是求泛函的极值。例如:一个在铅直平面的小球从高点A到达低点B,通过怎样的路径所用的时间最短?直觉上我们可能认为走A到B的线段最短,然而事实并非如此,这就是著名的的最速降线问题(也叫作捷线问题),后面会详细讲述这个问题。
一条两端固定自然悬挂的均质绳索,在重力作用下会呈现怎样的形状?这是有名的悬链线问题,本质上还是使得悬链线的重力势能最小化。光线在连续不均匀介质中的传播路径是怎样的?由于光在宏观上总是沿光程最短的路径传播,所实质上还是求泛函的最小值问题。
泛函相比与函数有很多不同的地方,因此求泛函的极值需要借助新的工具,然而从原理上,我们仍然可以借鉴求驻点的方法。我么考虑一个典型的泛函:
F
[
y
]
=
∫
a
b
f
(
x
,
y
,
y
′
)
d
x
F[y]=\int_a^bf(x,y,y')dx
F[y]=∫ab?f(x,y,y′)dx
并且有:函数
y
y
y在
a
和
b
a和b
a和b两端的值是固定的。
这里我们给定函数 y y y 附近任意一个微小的变化 δ y = y ? ? y \delta y=y^*-y δy=y??y,(类似 Δ x = x ′ ? x \Delta x=x'-x Δx=x′?x),我们称之为变分。考虑到泛函 F F F必须停驻,则泛函的变分 δ F = 0 \delta F=0 δF=0.现在我们推导 δ F \delta F δF的表达式:
δ
F
=
F
[
y
+
δ
y
]
?
F
(
y
)
\delta F=F[y+\delta y]-F(y)
δF=F[y+δy]?F(y)
=
∫
a
b
f
(
x
,
y
+
δ
y
,
y
′
+
δ
y
′
)
d
x
?
∫
a
b
f
(
x
,
y
,
y
′
)
d
x
=\int_a^b f(x,y+\delta y,y'+\delta y')dx-\int_a^bf(x,y,y')dx
=∫ab?f(x,y+δy,y′+δy′)dx?∫ab?f(x,y,y′)dx
泰勒展开保留第一项
=
∫
a
b
[
f
(
x
,
y
,
y
′
)
+
?
f
?
y
d
y
+
?
f
?
y
′
d
y
′
]
d
x
?
∫
a
b
f
(
x
,
y
,
y
′
)
d
x
=\int_a^b[f(x,y,y')+\frac{\partial f}{\partial y}dy+\frac{\partial f}{\partial y'}dy']dx-\int_a^bf(x,y,y')dx
=∫ab?[f(x,y,y′)+?y?f?dy+?y′?f?dy′]dx?∫ab?f(x,y,y′)dx
=
∫
a
b
[
?
f
?
y
d
y
+
?
f
?
y
′
d
y
′
]
d
x
=\int_a^b[\frac{\partial f}{\partial y}dy+\frac{\partial f}{\partial y'}dy']dx
=∫ab?[?y?f?dy+?y′?f?dy′]dx
使用分部积分
=
[
?
f
?
y
′
δ
y
]
∣
a
b
+
∫
a
b
[
?
f
?
y
?
d
d
x
(
?
f
?
y
′
)
δ
y
]
d
x
=[\frac{\partial f}{\partial y'}\delta y]|_a^b+\int_a^b[\frac{\partial f}{\partial y}-\frac{d}{dx}(\frac{\partial f}{\partial y'})\delta y]dx
=[?y′?f?δy]∣ab?+∫ab?[?y?f??dxd?(?y′?f?)δy]dx
=
∫
a
b
[
?
f
?
y
?
d
d
x
(
?
f
?
y
′
)
]
δ
y
d
x
=\int_a^b[\frac{\partial f}{\partial y}-\frac{d}{dx}(\frac{\partial f}{\partial y'})]\delta ydx
=∫ab?[?y?f??dxd?(?y′?f?)]δydx
在
a
a
a 和
b
b
b 两端点处有
δ
y
=
0
\delta y=0
δy=0,是因为在这里函数
y
(
x
)
y(x)
y(x)是固定的。上式中对于任意的可能变分
δ
y
(
x
)
\delta y(x)
δy(x)要使得
δ
F
=
0
\delta F=0
δF=0 ,当且仅当:
?
f
?
y
=
d
d
x
(
?
f
?
y
′
)
\frac{\partial f}{\partial y}=\frac{d}{dx}(\frac{\partial f}{\partial y'})
?y?f?=dxd?(?y′?f?)
这就是欧拉-拉格朗日方程,也是通过变分原理求泛函极值应用最广的方程。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!