【推荐系统】推荐算法数学基础

2023-12-15 12:34:56

【大家好，我是爱干饭的猿，本文重点介绍推荐系统涉及的数学知识、推荐系统涉及的概率统计知识。
后续会继续分享其他重要知识点总结，如果喜欢这篇文章，点个赞👍，关注一下吧】

上一篇文章：《【推荐系统】了解推荐系统的生态（重点：推荐算法的主要分类）》

2. 推荐算法数学基础

本章回顾并梳理了学习算法必需的数学知识和统计学知识，帮助大家巩固基础，平滑过渡，为后面学习推荐算法做铺垫。

汗流浃背了吧老弟，全是大学高数和概率论知识！！！

2.1 推荐系统涉及的数学知识

向量

  • 既有长度又有方向
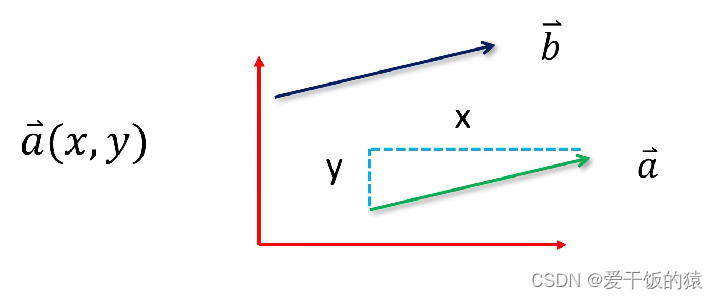
    在这里插入图片描述

向量和矩阵的关系

  • 由有限个向量组可以构成一个矩阵
  • 向量是矩阵的—部分

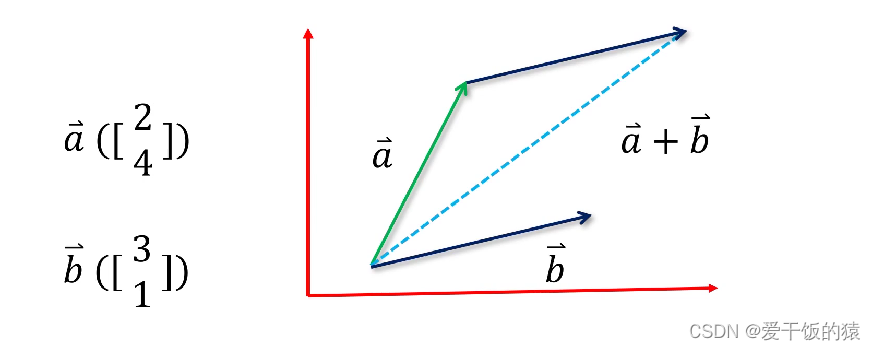
在这里插入图片描述

向量的和

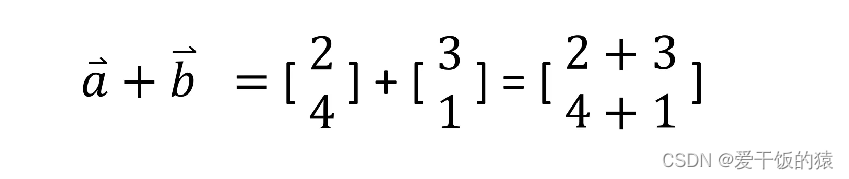
在这里插入图片描述
在这里插入图片描述

向量和常量的乘法

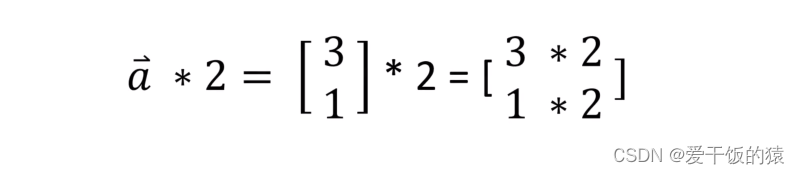
在这里插入图片描述
在这里插入图片描述

向量乘积

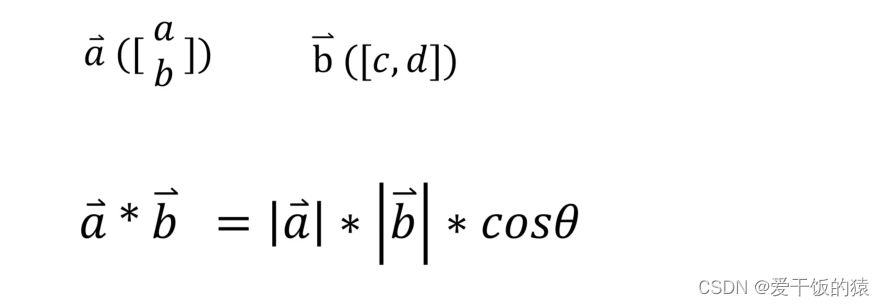
在这里插入图片描述

矩阵与矩阵相乘

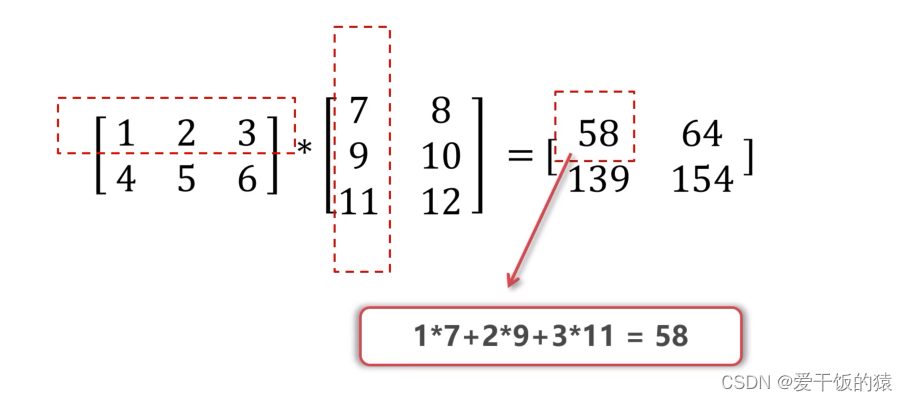
在这里插入图片描述

  • 第一个矩阵的列数必须等于第二个矩阵的行数
  • 相乘获得的矩阵行数是第一个矩阵的行数，列数是第二个矩阵的列数

矩阵

  • 方阵，单位矩阵
  • 矩阵的转置:A^T
  • 矩阵的逆矩阵:A^-1
  • 矩阵的秩

导数

  • 导数是用来分析变化的
  • 一次函数（直线)的求导，得到的是斜率
  • 二次函数（曲线)的求导，得到的是各点切线的斜率

偏导数

  • 当存在多个自变量和一个因变量
  • 假设其他自变量不变
  • 当只有一个自变量变化时，因变量也会随之变化

方向导数

  • 一个函数沿指定方向的变化率

梯度

  • 梯度是偏导向量的方向
  • 沿着偏导向量的方向导数能够取得最大值
  • 梯度就是变化最快的方向

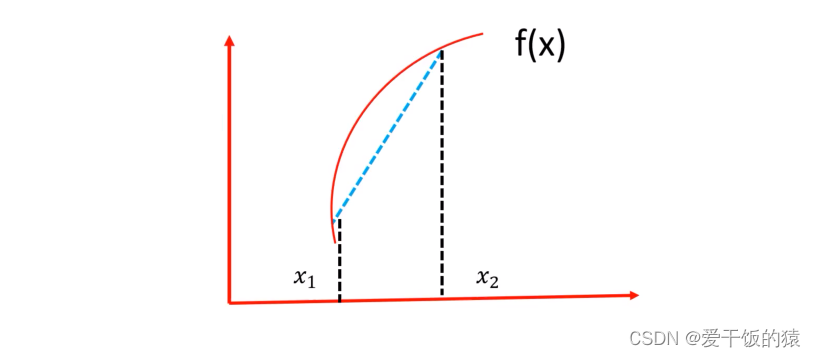
凸函数和凹函数

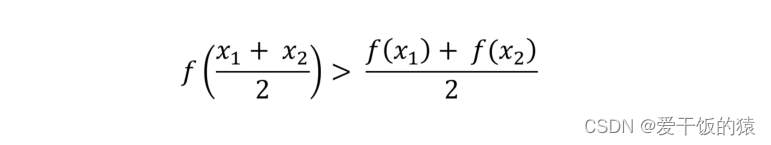
在这里插入图片描述

在这里插入图片描述

2.2 推荐系统涉及的概率统计知识

均值

  • 反映一组数据集中趋势的统计量
  • 算术平均数、加权平均数、中位数

数学期望

  • 掷骰子游戏，规定掷出1点得到1元，2点得到2元，以此类推
  • 求:掷一次它的期望值
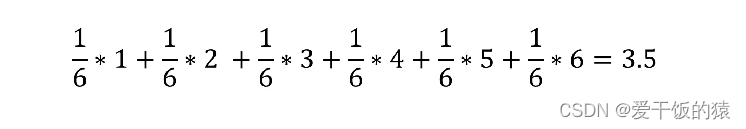
    在这里插入图片描述

方差

  • 方差是一种特殊的期望
  • 是衡量源数据和期望值相差的度量值
  • 方差是计算每一个观察值和总体均数之间的差异
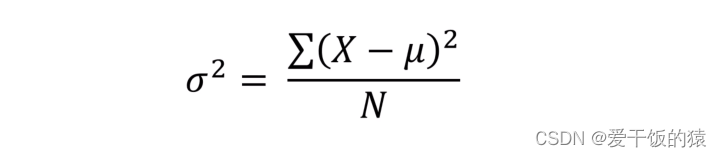
    在这里插入图片描述
  • A: 40,100,120,70,30。平均成绩=72
  • B: 73,70,72,75,70。平均成绩= 72

样本标准差

  • 样本标准差=方差的算术平方根
  • 方差是数据的平方，与检测值本身相差太大，难以直观的衡量

协方差

  • 协方差是度量两个随机变量关系的统计量
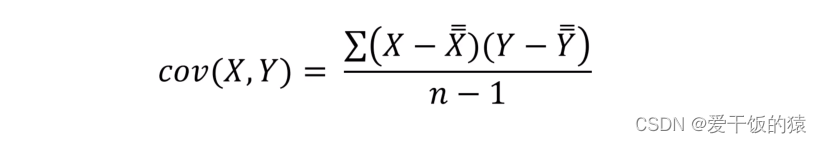
    在这里插入图片描述

相关系数

  • X、Y的协方差除以X的标准差和Y的标准差的乘积
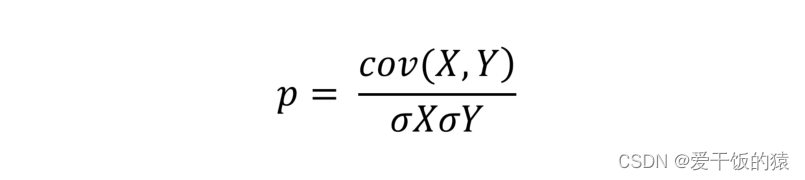
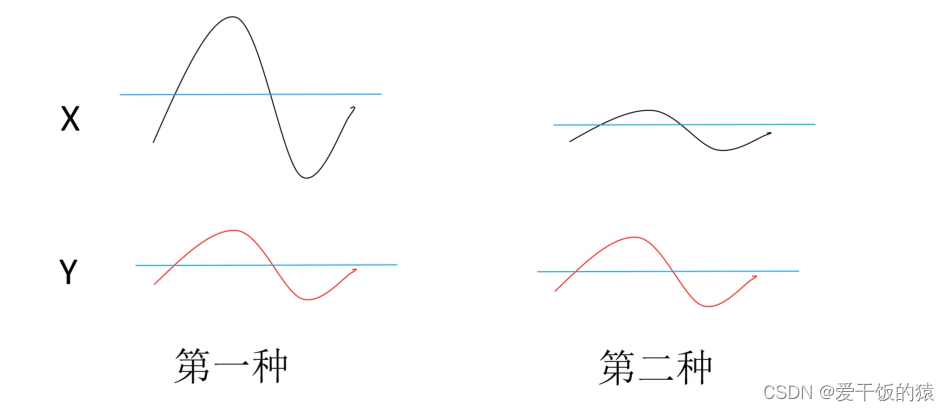
    在这里插入图片描述
    在这里插入图片描述

概率密度函数

  • 离散型变量:取值可以——列出，且总数确定

  • 连续型变量:取值无法——列出，且总数不确定

  • 概率分布:给出了所有值及其概率，只对离散型变量有意义

  • 概率函数:是对概率分布的描述，只对离散型变量有意义

  • 概率分布函数:给出了x落在某区间内的概率

  • 概率密度函数:给出了x落在某区间内的概率变化快慢

均匀分布

  • 任意相同间隔所对应的概率分布都相等
    在这里插入图片描述

正态分布（高斯分布）

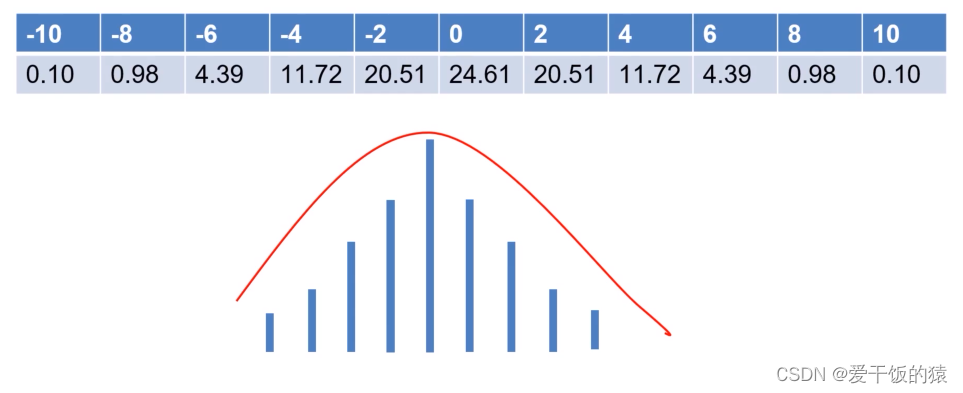
在这里插入图片描述

中心极限定理

  • 正太分布为什么常见，原因是中心极限定理
  • 大量相互独立的随机变量，当采样次数足够大
  • 不管随机变量呈现什么分布，抽取样本的均值接近正太分布

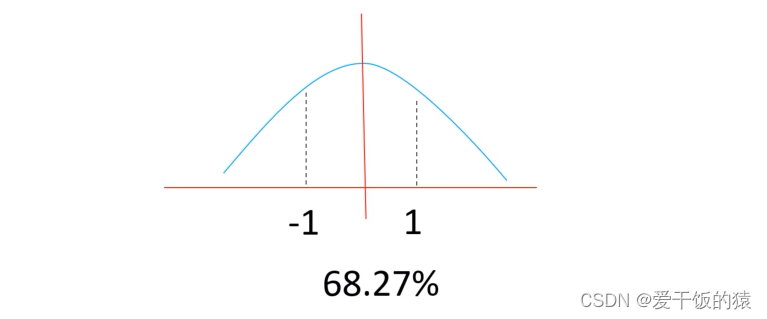
置信区间

  • 标准正太分布是均值为0，标准差为1
    在这里插入图片描述

条件概率公式

  • A，B是两个事件，在B发生的条件下，A发生的概率
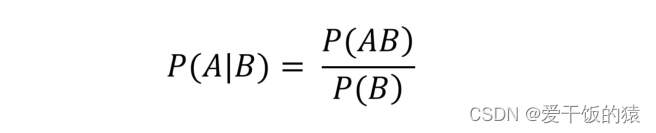
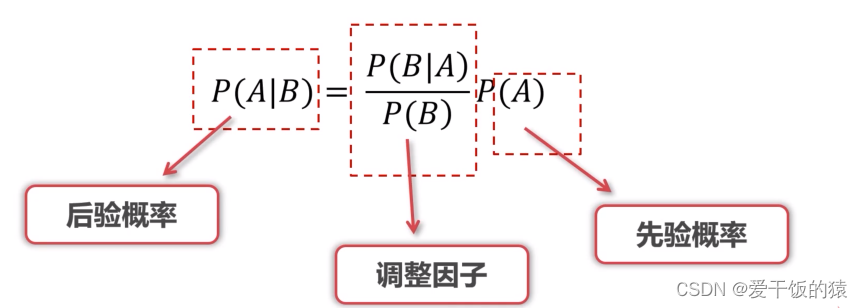
    在这里插入图片描述

贝叶斯公式

  • 贝叶斯公式就是建立在条件概率基础上寻找事件发生的原因
    在这里插入图片描述

文章来源:https://blog.csdn.net/m0_62218217/article/details/134870202
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。