Time-series forecasting with deep learning: a survey

??

? 人们开发了许多深度学习架构来适应不同领域的时间序列数据集的多样性。在本文中，我们调查了一步前进和多水平时间序列预测中使用的常见编码器和解码器设计，描述了如何将时间信息纳入每个模型的预测中。接下来，我们重点介绍混合深度学习模型的最新发展，该模型将经过充分研究的统计模型与神经网络组件相结合，以改进任一类别的纯方法。最后，我们概述了深度学习也可以通过时间序列数据促进决策支持的一些方法。本文是主题“天气和气候建模的机器学习”的一部分。

1. Introduction?

??时间序列建模历来是学术研究的一个关键领域，是气候建模 [1]、生物科学 [2] 和医学 [3] 以及零售业商业决策等主题应用不可或缺的一部分 [ 4] 和金融 [5] 等等。虽然传统方法侧重于由领域专业知识提供的参数模型，例如自回归 (AR) [6]、指数平滑 [7,8] 或结构时间序列模型 [9]，但现代机器学习方法提供了一种学习时间动态的方法以纯粹数据驱动的方式[10]。随着近年来数据可用性和计算能力的不断提高，机器学习已成为下一代时间序列预测模型的重要组成部分。受图像分类[11]、自然语言处理[12]和强化学习[13]。通过结合反映底层数据集细微差别的定制架构假设（或归纳偏差 [14]），深度神经网络能够学习复杂的数据表示 [15]，从而减轻了手动特征工程和模型设计的需要。开源反向传播框架[16,17]的可用性也简化了网络训练，允许定制网络组件和损失函数。

? ??鉴于各个领域的时间序列问题的多样性，出现了许多神经网络设计选择。在本文中，我们总结了使用深度神经网络进行时间序列预测的常见方法。首先，我们描述了可用于常见预测问题的最先进技术，例如多水平预测和不确定性估计。其次，我们分析了混合模型新趋势的出现，该模型将特定领域的定量模型与深度学习组件相结合以提高预测性能。接下来，我们概述了神经网络可用于促进决策支持的两种关键方法，特别是通过可解释性和反事实预测的方法。最后，我们总结了时间序列预测深度学习的一些有前景的未来研究方向——特别是连续时间和分层模型的形式。

? ?虽然我们努力提供深度学习现代方法的全面概述，但我们注意到我们的调查绝不是包罗万象的。事实上，关于时间序列预测的自动化方法存在丰富的文献，包括自动参数模型选择[18]，以及传统的机器学习方法，例如核回归[19]和支持向量回归[20]。此外，高斯过程[21]已广泛用于时间序列预测，最近的扩展包括深度高斯过程[22]，以及通过神经过程进行深度学习的并行[23]。此外，旧的神经网络模型历史上一直用于时间序列应用，如[24]和[25]中所示。

?2. Deep learning architectures for time-series forecasting

??时间序列预测模型预测给定实体 i 在时间 t 的目标 yi,t 的未来值。每个实体代表时间信息的逻辑分组，例如气候学中不同气象站的测量值，或医学中不同患者的生命体征，并且可以同时观察。在最简单的情况下，一步领先的预测模型采用以下形式

其中 ? yi,t+1 是模型预测，yi,t?k:t ={yi,t?k, ..., yi,t}, xi,t?k:t ={xi,t?k , ..., xi,t} 分别是在回溯窗口 k 上对目标输入和外源输入的观察，si 是与实体关联的静态元数据（例如传感器位置），f (.) 是学习的预测函数通过模型。虽然我们在本次调查中重点关注单变量预测（即一维目标），但我们注意到相同的组件可以扩展到多变量模型而不失一般性[26-30]。为了符号简单起见，除非明确要求，否则我们在后续部分中省略实体索引 i。

(a) Basic building blocks

??深度神经网络通过使用一系列非线性层构建中间特征表示来学习预测关系[15]。在时间序列设置中，这可以视为将相关历史信息编码到潜在变量 zt 中，并单独使用 zt 生成最终预测

其中genc(.)、gdec(.)分别是编码器和解码器函数，并回顾方程(2.1)中的下标i被删除以简化符号（例如，yi,t被yt替换）。因此，这些编码器和解码器构成了深度学习架构的基本构建块，可以选择网络确定我们的模型可以学习的关系类型。在本节中，我们将研究编码器的现代设计选择（如图 1 所示），以及它们与传统时间模型的关系。此外，我们还探讨了时间序列预测应用程序中使用的常见网络输出和损失函数。

(i) Convolutional neural networks

??传统上为图像数据集设计的卷积神经网络（CNN）提取在空间维度上不变的局部关系[11,31]。为了使 CNN 适应时间序列数据集，研究人员使用多层因果卷积 [32-34]，即卷积滤波器旨在确保仅使用过去的信息进行预测。对于隐藏层 l 的中间特征，每个因果卷积滤波器采用以下形式

?其中 hlt ∈ RHin 是第 l 层在时间 t 的中间状态，* 是卷积算子，W(l, τ ) ∈ RHout×Hin 是第 l 层的固定滤波器权重，A(.) 是激活函数，这样作为 sigmoid 函数，代表任何特定于架构的非线性处理。对于总共使用 L 个卷积层的 CNN，我们注意到编码器输出为 zt = htL。

??考虑一维情况，我们可以看到方程（2.5）与数字信号处理中的有限脉冲响应（FIR）滤波器非常相似[35]。这对 CNN 学习的时间关系产生了两个关键影响。首先，与标准 CNN 的空间不变性假设一致，时间 CNN 假设关系是时间不变的——在每个时间步长和所有时间都使用相同的一组滤波器权重。此外，CNN 只能使用其定义的回溯窗口或感受野内的输入来进行预测。因此，需要仔细调整感受野大小 k，以确保模型可以利用所有相关的历史信息。值得注意的是，单个因果 CNN 层相当于 AR 模型。

? ?扩张卷积。在长期依赖性很重要的情况下，使用标准卷积层在计算上可能具有挑战性，因为参数的数量直接随着感受野的大小而变化。为了缓解这个问题，现代架构经常使用扩张的协卷积层[32,33]，它将方程（2.5）扩展如下

?。是楼层运算符，dl 是特定于层的膨胀率。因此，扩张卷积可以解释为下层特征的下采样版本的卷积，降低分辨率以合并来自遥远过去的信息。因此，通过增加随着每层的扩张率，扩张卷积可以逐渐聚合不同时间块的信息，从而允许以有效的方式使用更多历史记录。以 [32] 的 WaveNet 架构为例，膨胀率以 2 的幂增加，相邻时间块在每层中聚合，从而允许在第 l 层使用 2l 个时间步长，如图 1a 所示。

??

(ii) Recurrent neural networks?

??递归神经网络（RNN）历来被用于序列建模[31]，在各种自然语言处理任务上取得了很好的结果[36]。鉴于时间序列数据作为输入和目标序列的自然解释，许多基于 RNN 的架构已被开发用于时间预测应用 [37-40]。 RNN 单元的核心包含一个内部记忆状态，它充当过去信息的紧凑摘要。如图 1b 所示，每个时间步都会用新的观察结果递归更新记忆状态，即

其中 zt ∈ RH 这里是 RNN 的隐藏内部状态，ν(.) 是学习到的记忆更新函数。例如，Elman RNN [41]，最简单的 RNN 变体之一，将采用以下形式

其中 W., b.分别是网络的线性权重和偏差，γy(.)、γz(.)是网络激活函数。请注意，RNN 不需要按照 CNN 的情况明确指定回溯窗口。从信号处理的角度来看，主要的循环层，即方程（2.9）——因此类似于无限脉冲响应（IIR）滤波器的非线性版本。

? ?长短期记忆 由于无限回溯窗口，RNN 的旧变体在学习数据中的长期依赖性方面可能会受到限制 [42,43]——由于梯度爆炸和消失的问题 [31]。直观上，这可以看作是记忆状态共振的一种形式。因此，开发了长短期记忆网络（LSTM）[44]，通过改进网络内的梯度流来解决这些限制。这是通过使用存储长期信息的单元状态 ct 来实现的，并通过一系列门进行调制，如下所示

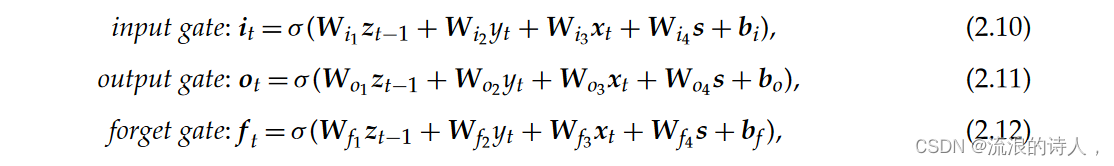
?其中 zt?1 是 LSTM 的隐藏状态，σ (.) 是 sigmoid 激活函数。门修改 LSTM 的隐藏状态和单元状态，如下所示

?其中 是元素级 (Hadamard) 乘积，tanh(.) 是 tanh 激活函数。与贝叶斯过滤的关系 正如 [39] 中所研究的，贝叶斯过滤器 [45] 和 RNN 在维护隐藏状态方面都很相似，隐藏状态会随着时间的推移而递归更新。对于贝叶斯滤波器，例如卡尔曼滤波器[46]，通过使用一系列状态转换和纠错步骤更新潜在状态的足够统计数据来执行推理。由于贝叶斯过滤步骤使用确定性方程来修改足够的统计量，因此 RNN 可以被视为两个步骤的同时近似，其中记忆向量包含预测所需的所有相关信息。

(iii) Attention mechanisms

注意力机制的发展[47??,48]也导致了长期依赖学习的改进——变压器架构在多种自然语言处理应用中实现了最先进的性能[12,49,50]。注意力层使用动态生成的权重聚合时间特征（图 1c），允许网络直接关注过去的重要时间步骤——即使它们在回溯窗口中非常遥远。从概念上讲，注意力是一种基于给定查询的键值查找机制[51]，采用以下形式

其中键 κt、queryqτ 和值 vt?τ 是网络较低层在不同时间步产生的中间特征。此外，α(κt, qτ ) ε [0, 1] 是在时间 t 生成的 t ? τ 的注意力权重，ht 是注意力层的上下文向量输出。请注意，根据 CNN 情况，多个注意力层也可以一起使用，最后一层的输出形成编码的潜在变量 zt。

??最近的工作还证明了在时间序列预测应用中使用注意力机制的好处，其性能优于可比较的循环网络[52-54]。例如，[52]使用注意力来聚合 RNN 编码器提取的特征，注意力权重如下所示

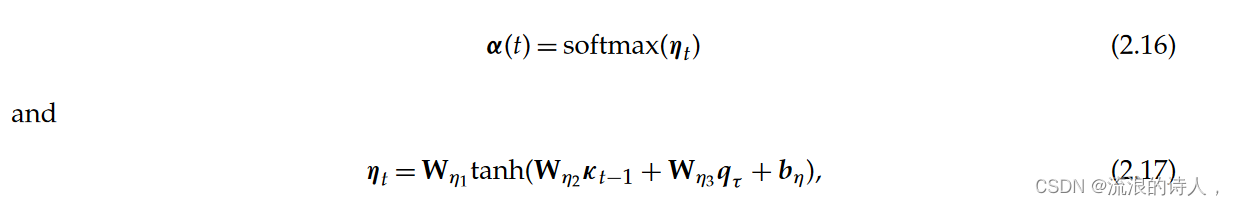
?其中 α(t) = [α(t,0),...α(t, k)] 是注意力权重向量，κt?1, qt 是用于特征提取的 LSTM 编码器的输出，softmax(. ) 是 softmax 激活函数。最近，[53,54]中也考虑了变压器架构，它将标量点积自注意力[49]应用于回溯窗口内提取的特征。从时间序列建模的角度来看，注意力提供了两个主要好处。首先，具有注意力的网络能够直接关注发生的任何重大事件。例如，在零售预测应用中，这包括可能对销售产生积极影响的假期或促销期。其次，如[54]所示，基于注意力的网络还可以通过为每个机制使用不同的注意力权重模式来学习特定于机制的时间动态。

(iv) Outputs and loss functions

? ?鉴于神经网络的灵活性，深度神经网络已被用于对离散[55]和连续[37,56]目标进行建模——通过定制神经网络的解码器和输出层来匹配所需的目标类型。在一步领先的预测问题中，这可以像将编码器输出的线性变换（即方程（2.2））与目标的适当输出激活相结合一样简单。无论目标的形式如何，预测都可以进一步分为两个不同的类别：点估计和概率预测。点估计 预测的常见方法是确定未来目标的预期值。这本质上涉及使用上述编码器将问题重新表述为离散输出的分类任务（例如预测未来事件）和连续输出的回归任务。对于二元分类情况，解码器的最后一层具有带有 sigmoid 激活函数的线性层，允许网络预测给定时间步长事件发生的概率。对于二进制和的一步预测连续目标，分别使用二元交叉熵和均方误差损失函数来训练网络

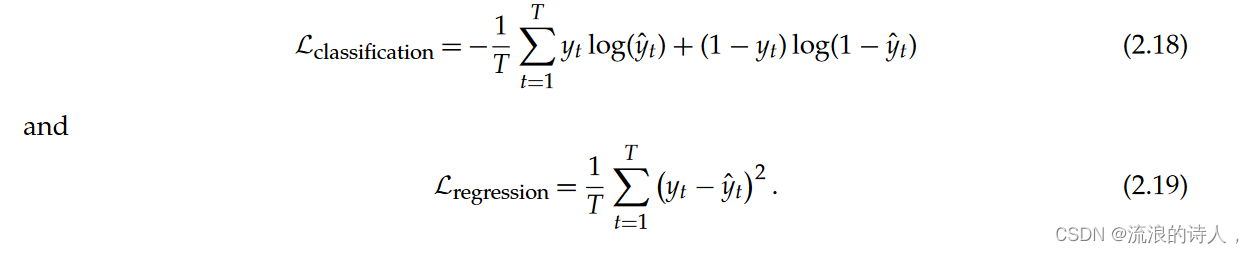
虽然上述损失函数在应用中最常见，但我们注意到神经网络的灵活性也允许采用更复杂的损失，例如分位数回归[56]和多项分类[32]的损失。概率输出虽然点估计对于预测目标的未来价值至关重要，但了解模型预测的不确定性对于不同领域的决策者可能很有用。例如，当预测不确定性很大时，模型用户在将预测纳入决策时可以更加谨慎，或者依赖其他信息来源。在某些应用中，例如金融风险管理，访问完整的预测分布将允许决策者在出现罕见事件（例如，意外事件）时优化其行动。允许风险管理者使投资组合免受市场崩溃的影响。建模不确定性的常见方法是使用深度神经网络生成已知分布的参数[27,37,38]。例如，高斯分布通常用于预测连续目标的问题，网络在每一步输出预测分布的均值和方差参数，如下所示

?其中 htL 是网络的最后一层，softplus(.) 是 softplus 激活函数，以确保标准差仅取正值。

(b) Multi-horizon forecasting models

在许多应用中，在未来的多个点访问预测估计通常是有益的，允许决策者可视化未来范围内的趋势，并在整个路径上优化他们的行动。从统计角度来看，多水平预测可以看作是对一步超前预测问题（即方程（2.1））的轻微修改，如下所示

其中 τ ∈{1, ..., τmax} 是离散预测范围，ut 是整个范围内已知的未来输入（例如日期信息，例如星期几或月份），xt 是可以只能从历史上观察。与传统的计量经济学方法[57,58]一致，用于多水平预测的深度学习架构可以分为迭代方法和直接方法——如图2所示，并在下面详细描述。

?(i) Iterative methods

??多水平预测的迭代方法通常利用 AR 深度学习架构 [37,39,40,53]，通过将目标样本递归地输入到未来的时间步长中来生成多水平预测（图 2a）。通过重复该过程来生成多个轨迹，然后使用每一步目标值的采样分布来生成预测。例如，可以使用蒙特卡罗估计获得预测平均值yt+τ = ΣJ j=1 ? y(j) t+τ /J，其中 ? y(j) t+τ 是根据式（2.20）模型抽取的样本。由于 AR 模型的训练方式与一步预测模型完全相同（即通过时间反向传播），因此迭代方法可以轻松地将标准模型推广到多步预测。然而，由于每个时间步长都会产生少量误差，迭代方法的递归结构可能会导致较长预测范围内的较大误差累积。此外，迭代方法假设除目标之外的所有输入在运行时都是已知的，仅需要将目标的样本输入到未来的时间步骤中。在许多存在观察输入的实际场景中，这可能是一个限制，从而激发了对更灵活方法的需求。

?(ii) Direct methods

??直接方法通过使用所有可用输入直接生成预测来缓解迭代方法的问题。它们通常利用序列到序列架构[52,54,56]，使用编码器来总结过去的信息（即目标、观察到的输入和先验输入），并使用解码器将它们与已知的未来输入相结合——如图所示如图 2b 所示。正如[59]中所述，另一种方法是使用更简单的模型直接生成与所需预测范围匹配的固定长度向量。然而，这确实需要指定最大预测范围（即 τmax），并且仅在预定义的离散间隔内进行预测。

3. Incorporating domain knowledge with hybrid models

??尽管机器学习很受欢迎，但它在时间序列预测方面的有效性历来受到质疑——M-竞赛等预测竞赛就证明了这一点[60]。在 2018 年 M4 竞赛之前 [61]，普遍的观点是复杂的方法不会产生更准确的预测，而具有集成的简单模型往往会做得更好 [59,62,63]。已经确定了两个关键原因来解释机器方法表现不佳的原因。首先，机器学习方法的灵活性可能是一把双刃剑——使它们容易过度拟合[59]。因此，更简单的模型可能在低数据情况下表现更好，这在使用少量历史观察数据（例如季度宏观经济预测）来预测问题时尤其常见。其次，与统计模型的平稳性要求类似，机器学习模型可以对输入的预处理方式敏感[26,37,59]，这确保训练和测试时的数据分布相似。

? ?深度学习的最新趋势是开发解决这些局限性的混合模型，在各种应用中展示出比纯统计或机器学习模型更高的性能[38,64–66]。混合方法将经过充分研究的定量时间序列模型与深度学习相结合——使用深度神经网络在每个时间步生成模型参数。一方面，混合模型允许领域专家使用先验信息来通知神经网络训练——减少网络的假设空间并提高泛化能力。这对于小型数据集 [38] 特别有用，因为深度学习模型过度拟合的风险更大。此外，混合模型允许固定和非固定组件的分离，并避免需要自定义输入预处理。这方面的一个例子是指数平滑 RNN（ES-RNN）[64]，它是 M4 竞赛的获胜者，它使用指数平滑来捕获非平稳趋势并通过 RNN 学习附加效果。一般来说，混合模型以两种方式使用深度神经网络：a）为非概率参数模型编码时变参数[64,65,67]，b）为概率模型生成分布参数[38,40， 66]。

??(a) Non-probabilistic hybrid models

??使用参数时间序列模型，预测方程通常通过分析方式定义，并为未来目标提供点预测。因此，非概率混合模型修改这些预测方程以结合统计和深度学习组件。例如，ES-RNN 使用 Holt–Winters 指数平滑模型 [8] 的更新方程，将乘性水平和季节性分量与深度学习输出相结合，如下所示

其中 hiL,t+τ 是 τ 步提前预测的网络最后一层，li,t 是水平分量，γi,t 是周期性分量，周期??为 κ,β(i) 1 , β( i) 2 是实体特定的静态系数。从上面的方程中，我们可以看到指数平滑分量（li，t，γi，t）处理数据集中更广泛的（例如指数）趋势，减少了额外输入缩放的需要。

(b) Probabilistic hybrid models

概率混合模型还可以用于分布建模很重要的应用中——使用概率生成模型进行时间动态，例如高斯过程[40]和线性状态空间模型[38]。概率混合模型不是修改预测方程，而是使用神经网络在每一步生成预测分布的参数。例如，深度状态空间模型 [38] 对线性状态空间模型的时变参数进行编码，如下所示 - 通过卡尔曼滤波方程 [46] 进行推理

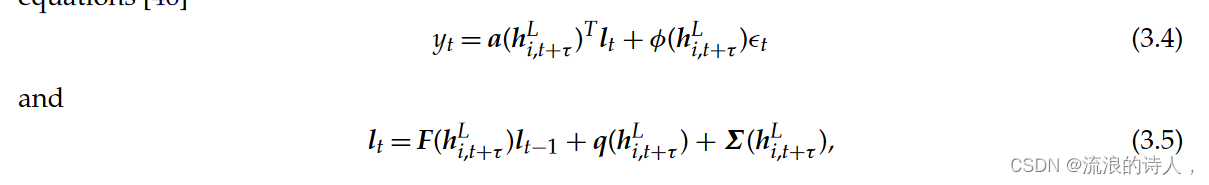
其中 lt 是隐藏的潜在状态，a(.)、F(.)、q(.) 是 hiL 的线性变换，t+τ 、 φ(.)、Σ(.) 是具有 softmax 激活的线性变换，t ～ N(0, 1), Σt ～ N(0, I) 是标准正态随机变量。

4. Facilitating decision support using deep neural networks

尽管模型构建者主要关心预测的准确性，但最终用户通常使用预测来指导他们未来的行动。例如，医生可以利用临床预测（例如疾病发病和死亡的概率）帮助他们确定测试的优先顺序、制定诊断并确定治疗方案。因此，虽然时间序列预测是至关重要的初步步骤，但更好地理解时间动态和模型预测背后的动机可以帮助用户进一步优化他们的行动。在本节中，我们将探讨神经网络扩展以促进时间序列数据决策支持的两个方向——重点关注可解释性和因果推理的方法。

(a) Interpretability with time-series data

随着神经网络在关键任务应用中的部署[68]，越来越需要了解模型如何以及为何做出某种预测。此外，随着近年来数据集的规模和复杂性不断增长，最终用户对其数据中存在的关系几乎没有先验知识。鉴于标准神经网络架构的黑盒性质，在解释深度学习模型的方法方面出现了新的研究主体，我们将在下面深入介绍。

??事后可解释性技术事后可解释模型的开发是为了解释经过训练的网络，并帮助识别重要的特征或示例，而无需修改原始权重。方法主要可以分为两大类。首先，一种可能的方法是在神经网络的输入和输出之间应用更简单的可解释代理模型，并依靠近似模型来提供解释。例如，局部可解释模型不可知的解释（LIME）[69]通过将特定于实例的线性模型拟合到输入的扰动来识别相关特征，其中线性系数提供了重要性的度量。 Shapley 附加解释 (SHAP) [70] 提供了另一种替代方法，该方法使用合作博弈论中的 Shapley 值来识别数据集中的重要特征。接下来，提出了基于梯度的方法，例如显着图[71,72]和影响函数[73]，它们分析网络梯度以确定哪些输入特征对损失函数影响最大。虽然事后可解释性方法可以帮助进行特征归因，但它们通常会忽略输入之间的任何顺序依赖性，从而很难将它们应用于复杂的时间序列数据集。

? ??具有注意力权重的固有可解释性另一种方法是直接设计具有可解释组件的架构，通常采用战略性放置的注意力层的形式。由于注意力权重是作为 softmax 层的输出产生的，因此权重之和被限制为 1，即 Σ τk=0 α(t, τ ) = 1。对于时间序列模型，方程 (2.15) 的输出因此可以也可以解释为时间特征的加权平均值，使用每一步注意力层提供的权重。然后可以使用注意力权重分析来了解每个时间步骤的特征的相对重要性。 [53,55,74]中已经进行了实例方面的可解释性研究，其中作者使用具体示例来展示 α(t, τ ) 的大小如何指示哪些时间点对于预测最重要。通过分析注意力向量随时间的分布，[54] 还展示了如何使用注意力机制来识别数据集中持久的时间关系（例如季节性模式）。

? ?(b) Counterfactual predictions and causal inference over time

??除了了解网络学到的关系之外，深度学习还可以通过在观测数据集之外生成预测或反事实预测来帮助促进决策支持。反事实预测对于场景分析应用程序特别有用，允许用户评估不同的操作集如何影响目标轨迹。从历史角度来看，即确定如果发生不同的情况会发生什么，从预测角度来看，即确定采取哪些行动来优化未来结果，这都是有用的。

? ??虽然存在一大类深度学习方法用于估计静态设置中的因果效应[75-77]，但时间序列数据集的关键挑战是存在与时间相关的混杂效应。当可能影响目标的操作也以对目标的观察为条件时，由于循环依赖而出现这种情况。如果不对时间相关的混杂因素进行任何调整，直接的估计技术可能会导致有偏差的结果，如[78]所示。最近，基于统计技术的扩展和新损失函数的设计，出现了几种训练深度神经网络的方法，同时调整与时间相关的混杂。通过统计方法，[79]扩展了流行病学中边际结构模型的反处理概率加权（IPTW）方法——使用一组网络来估计治疗应用概率，并使用序列到序列模型来学习无偏预测。 [80]中的另一种方法扩展了 G 计算框架，使用深度学习对目标和动作的分布进行联合建模。此外，[81]中提出了新的损失函数，它采用领域对抗训练来学习患者病史的平衡表示。

?5. Conclusion and future directions

??随着近年来数据可用性和计算能力的增长，深度神经网络架构在预测跨多个领域的问题方面取得了巨大成功。在本文中，我们调查了用于时间序列预测的主要架构，重点介绍了神经网络设计中使用的关键构建块。我们研究它们如何结合时间信息进行一步预测，并描述如何扩展它们以用于多水平预测。此外，我们概述了混合深度学习模型的最新趋势，该模型结合了统计和深度学习组件，在任一类别中都优于纯方法。最后，我们总结了深度学习可以扩展以随着时间的推移改善决策支持的两种方法，重点关注可解释性和反事实预测的方法。

? ?尽管已经开发了大量用于时间序列预测的深度学习模型，但仍然存在一些局限性。首先，深度神经网络通常要求时间序列以规则的间隔离散化，这使得预测观测值可能丢失或以随机间隔到达的数据集变得困难。虽然已经通过神经常微分方程完成了一些关于连续时间模型的初步研究[82]，但还需要做更多的工作来将这项工作扩展到具有复杂输入（例如静态变量）的数据集，并将其与现有模型进行基准测试。此外，正如[83]中提到的，时间序列通常具有层次结构，在轨迹之间进行逻辑分组——例如在零售预测中，同一地区的产品销售可能会受到共同趋势的影响。因此，开发明确考虑此类层次结构的架构可能是一个有趣的研究方向，并且有可能提高现有单变量或多变量模型的预测性能