CGAL的主成分分析
????????此软件包提供了分析二维和三维对象集的功能。它提供了所有有界对象的轴对齐边界框、质心和主成分分析的计算,以及加权点集的重心。请注意,与大多数CGAL软件包不同,该软件包使用近似方法(特别是线性最小二乘拟合),并不旨在提供任何意义上的精确规范结果。
1、定义
????????一组对象的边界框是包含该集的长方体。轴对齐的边界框捕获集合中所有对象在其坐标系内的最大范围,即与坐标系的轴对齐的边框。轴对齐的边界框在几何算法中经常被用作数据集的一般位置的指示,用于显示、一次近似空间查询或空间索引目的。
????????一组物体的质心是它们的质心,即通过组成物体的所有点的坐标来计算其坐标的点。请注意,尽管质心的一般定义包含密度函数(因此也包含加权平均值),但当前的实现方式假设了均匀的密度(见下面为加权点定义的重心)。对于点集{X1,X2,…,XN}质心X’计算为
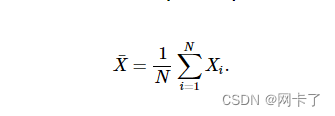
????????对于一组分段{S1,S2,…,SN}质心X’计算为
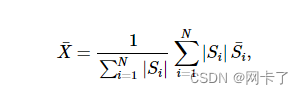
????????其中|Si|代表线段的长度,Si’代表其统一重心(中点)。对于一组三角形{T1,T2,…,TN}
质心X’计算为?

?
????????其中|Ti|表示三角形的面积,Tiˉ表示其均匀重心。对于更一般的对象,这种定义仍然适用,其中Lebesgue测度(1D中的长度,2D中的面积,3D中的体积)用于加权对象重心。质心用于汇总数据集,用于近似、空间查询或空间索引目的。
????????一组加权点的重心是坐标由该组所有加权点的加权坐标计算出来的点。当所有权重相等时,重心与质心重合。给定一组对象,线性最小二乘拟合相当于找到一个线性子空间,该线性子空间使组成该对象集的所有点与其投影到该线性子空间上的距离平方和最小化。这种线性子空间是通过所谓的主成分分析(PCA)获得的。
????????PCA被定义为将对象变换到新坐标系的一种变换,使得对象的正交投影的最大方差位于第一个坐标(称为第一主成分)上,第二个最大方差位于第二个坐标上,依此类推。PCA通常用于几何应用,以将数据集降低到较低的维度进行分析或近似。下图说明了(最小二乘)将一条直线拟合到二维点集,将一条直线和一个平面拟合到三维点集,以及将一个平面拟合到一组三维三角形。
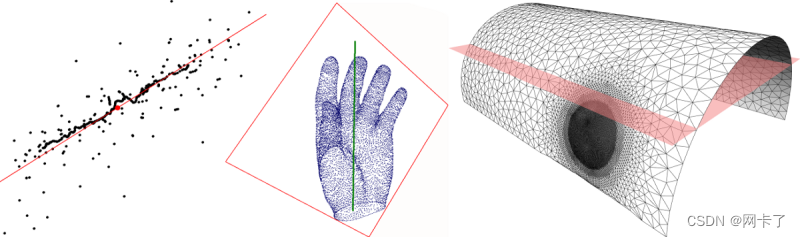
????????左图:将线拟合到二维点集(质心用红色点表示)。中间:将直线和平面拟合到三维点集。右图:将平面拟合到一组三维三角形。?
2、其他
????????在CGAL中,CGAL::centroid函数用于计算给定几何对象的质心。
????????质心是对象重心的数学表示。对于简单的几何对象(如点、线段、三角形等),质心是所有顶点坐标的平均值。对于更复杂的对象,质心是通过加权平均所有顶点坐标来计算的,其中权重通常是与每个顶点相关的体积或面积。
????????CGAL::barycenter 是一个函数,用于计算给定几何对象的重心。在CGAL库中,重心被定义为对象质量中心的加权平均位置。对于三角形,这个函数将返回一个点,该点的坐标是三角形三个顶点坐标的加权平均值。
????????CGAL::linear_least_squares_fitting_2 是一个函数,用于在二维空间中进行线性最小二乘拟合。它通过最小化所有点到拟合直线的垂直距离的平方和来找到最佳拟合直线。
????????质量中心简称质心,指物质系统上被认为质量集中于此的一个假想点。与重心不同的是,质心不一定要在有重力场的系统中。值得注意的是,除非重力场是均匀的,否则同一物质系统的质心与重心通常不在同一假想点上。
????????重心,是在重力场中,物体处于任何方位时所有各组成支点的重力的合力都通过的那一点。规则而密度均匀物体的重心就是它的几何中心。不规则物体的重心,可以用悬挂法来确定。物体的重心,不一定在物体上。另外,重心可以指事情的中心或主要部分。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!