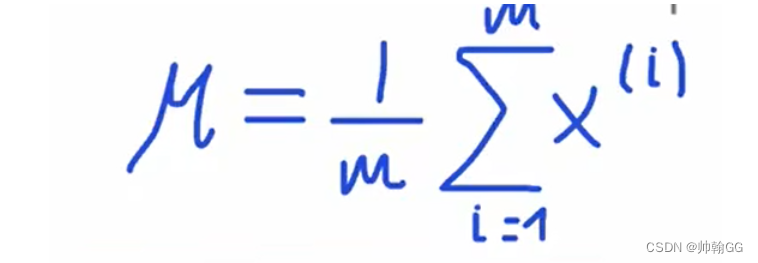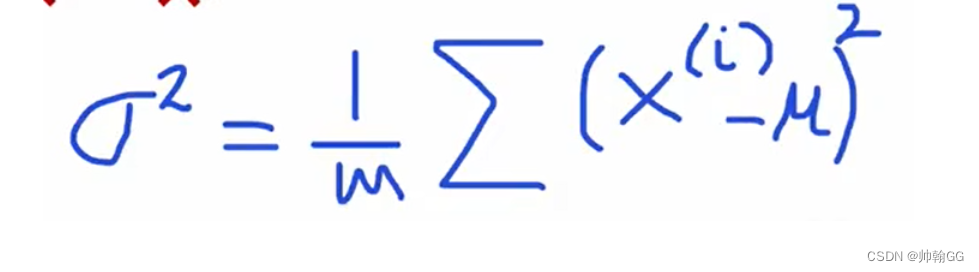C3-1.3.1 无监督学习——异常检测

C3-1.3.1 无监督学习——异常检测

1、举例：异常值检测示例——密度评估法

1.1 举一个例子

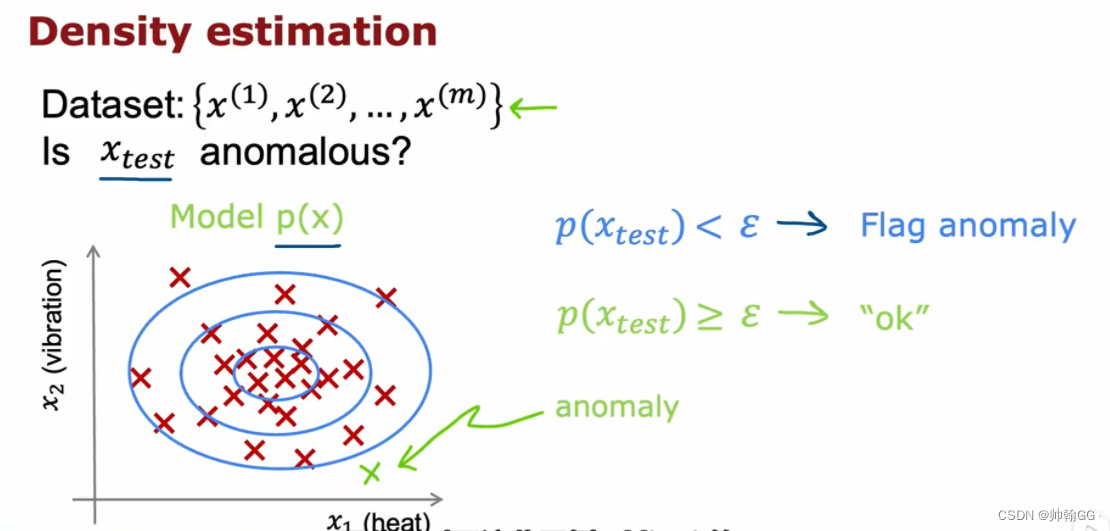
这里做的是 查看飞机发动机 异常检测：

• 左侧：X1 ,X2 … 是 可能会影响发动机状态的特征
• 右侧：
  • Dataset：训练数据集
  • New engine ：利用新发动机的数据来检测新建造出的发动机是否异常

• 这里只拿出来两个特征值（X1 , X2）来举例，为了可视化让我们了解的更加方便，实际应用中 特征的数量可能达到上百 / 上千

• 最外层蓝色圈内的：说明的大概率的，是正常的

• 最外层蓝色圈外的：是小概率发生的事件，要进行进一步的检查

• **P（X）：**这里通过训练集建立完成 模型 P(X)后，用训练集数据 X-test 来判断结果 P（X-test）：是否是状态异常的发动机

• **ε的值：**即最外圈蓝色框的概率的值

1.2 构建过程

• Step1：

  **特征的提取，**找出能够判断是否异常状态的特征——这里用的特征是：飞机发动机的热度X1,发动机震动频率X2

• Step2：

  ? 通过训练集的数据拟合出一个 模型——P(X)。

• Step3：

  ? 通过输入的数据 X （X可能是一组向量），得出概率值 y = P (X)。

  ? 如果：P(X) < ε (设定好的门槛值，这个值通常很小)，就说明发生异常

2、应用的算法：高斯正态分布

※※ 【核心】：高斯正态分布——很好的解释了：

• 上图中三个蓝色圈的由来 ？ / 代表什么？ /为什么要画这三个圈不是四个？
• P(x) Model 怎么拟合出来的？
• ε的值的也由来？

2.1、正态分布函数 / 高斯正态分布

• 3个蓝圈： 在 异常举例中，我们给出了3个蓝圈，其实每一个圈分别代表下面的三个分布的范围**（u± δ、u± 2δ、u± 3δ）**

• **P（x）：**也就是对应的高斯正态分布函数

• **ε的值的也由来：**为什么在 P（X）超过了 u - 3δ < P(X) < u + 3δ 的范围就认为他是异常值，因为在 u - 3δ < P(X) < u + 3δ 的范围（达到了99.7%）之外 的概率确实太小了。 ε =u± 3δ

? u - δ < P(X) < u + δ

? u - 2δ < P(X) < u + 2δ

? u - 3δ < P(X) < u + 3δ

• 均值u 的算法：

  • 

• 方差δ的算法：

  • 

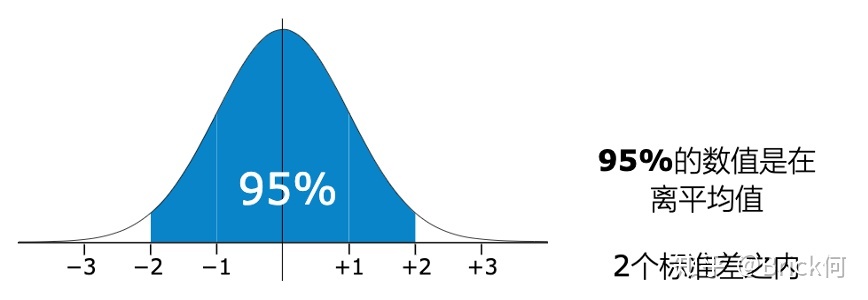
• 这个 “钟形”的概率分布的面积是 1。也就是说：

  • 标准差δ越小，意味着大多数变量值离均数的距离越短，因此大多数值都紧密地聚集在均数周围，图形呈现**“瘦高型”**
  • 相反，标准差δ越大，数据跨度就比较大，分散程度大，所覆盖的变量值就越多（比如1±0.5涵盖[0.5，1.5]），图形呈现**“矮胖型”** ——如图四

  

?

2.2 高斯分布的应用

• Step1 :通过训练集数据，进行散点分布在X轴上（这是训练其中的一个特征）：

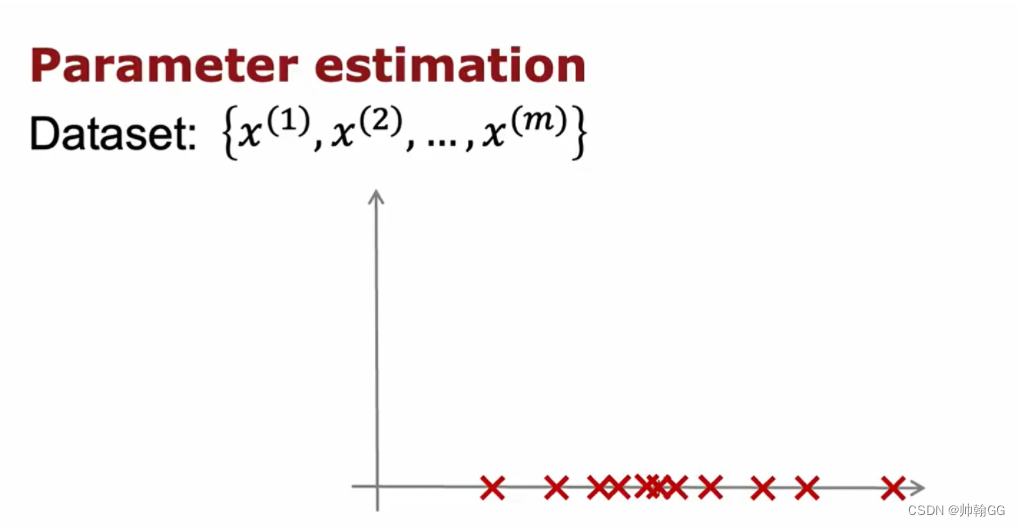
• Step 2 ： 正态分布的使用，进行X -> f(x)的映射：

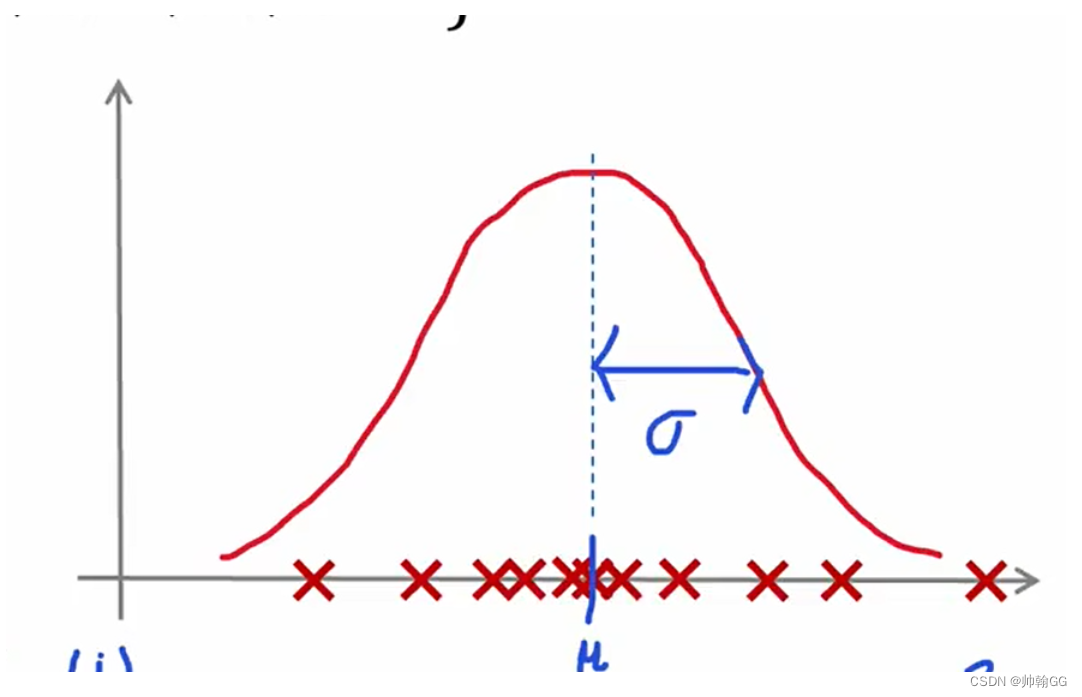
• Step 3 ：利用高斯分布进行 异常值的检测：

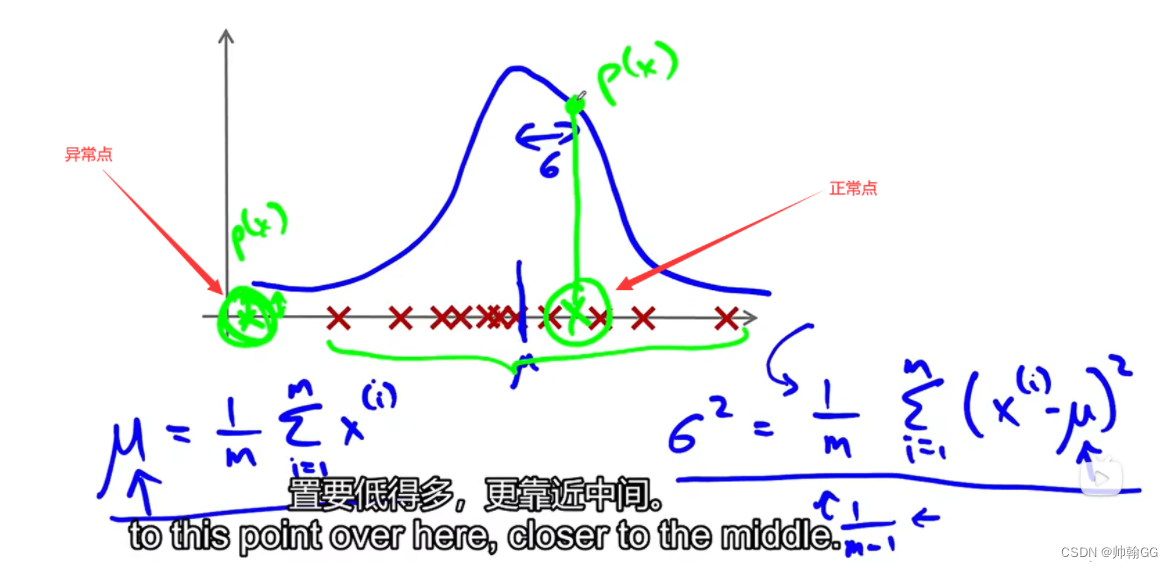
3、实现流程：异常检测算法实现流程

3.1、算法实现步骤

• Step1：
  • 选择可能影响最终结果——是否异常 的特征的选择
• Step 2：
  • **拟合模型，**训练每个特征向量对应的参数 —— u ； δ
• Step 3：
  • 通过输入测试集数据x-i，计算最终结果 P(x)

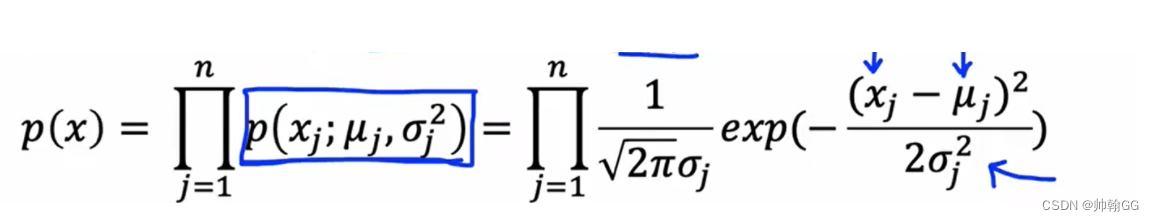
※P（X）是连乘得出的结果，是不同特征的特征值X 对应的P(X-i) 连乘 的结果，是每个特征对结果——异常检测的共同的影响

※P（X-i）中一旦有一个结果是不正常的——导致P(X-i)是特别小的数值——导致最终结果P(X)是特别小的数值——导致P(X)< u± 3δ ——得出结果是 异常点

ra%5Ctypora-user-images%5Cimage-20231101205906650.png&pos_id=img-QDV3Mm35-1704850973901)

【补充】：

• 均值 u的算法：

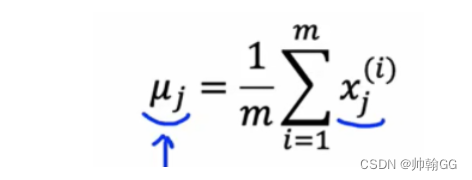
• 方差δ的算法：

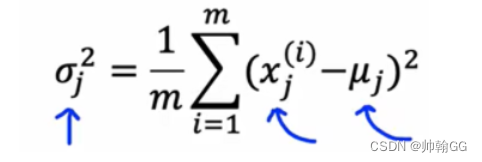
3.2 异常值检测实例

• Step1：
  • 选择可能影响最终结果——是否异常 的特征的选择
    • 这里是做 飞机发动机异常检测，保留了两个特征：
    • X1:发动机热度
    • X2：发动机震动频率
• Step 2：
  • **拟合模型，**训练每个特征向量对应的参数 —— u ； δ
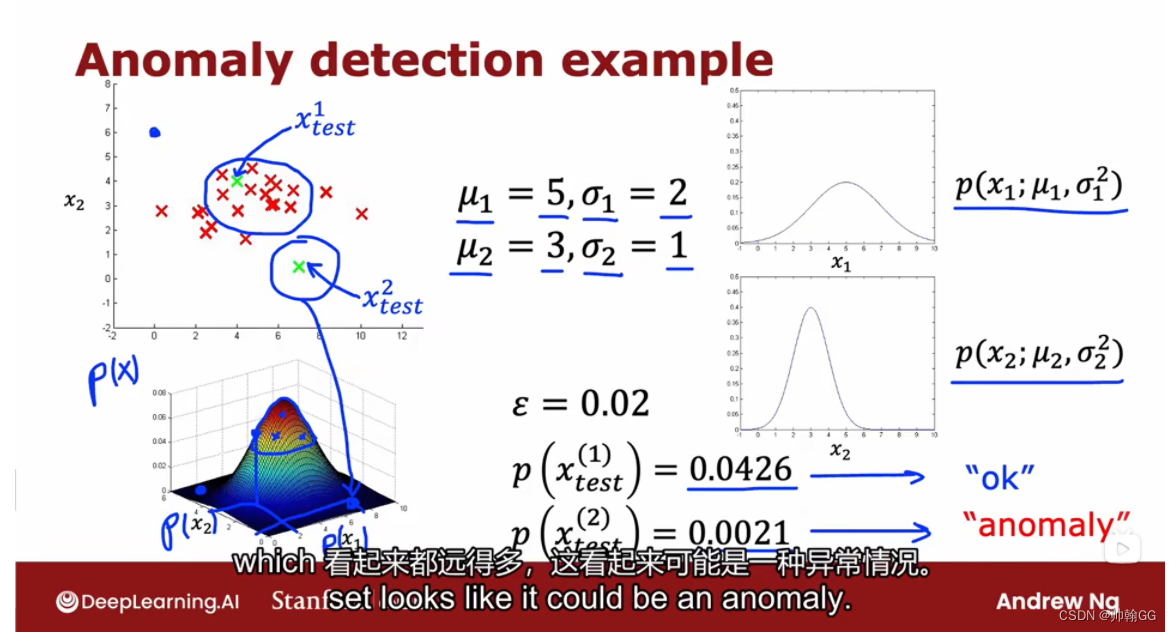
    • 计算得出 阀值 u± 3δ = ε = 0.02
    • 把 X1 ,X2 ，概率P 画在了三维图像上
• Step 3：
  • 通过输入测试集数据x-i，计算最终结果 P(x)
    • 从图中可以看出：
    • X1-test ：是正常值的状态
    • X2-test ：是异常状态，发生概率 P(X) < ε ，需要进一步对发动机做检测

4、模型微调：运用少量标签数据 改进算法的必要性

4.1、文章核心思想

【本节核心句子】： it’s turns out to be **very userful for turning(调整) the algorithm if you have a small number of anomalous examples so that you can create a cross validation set and a test set **,which i’m going to denote (x-cv(1),y-cv(1)) 、(x-cv(2),y-cv(2))，and have a test set of some number example where both the cross validation and test sets hopefully includes a few anomalous examples

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

4.2、应用的例子

• 给出了 10000个正常的数据 和 20个异常 / 瑕疵数据

• 给出两种方法去进行模型的训练

• 方法一：

  • 测试集用：6000个好的
  • 交叉验证集：用2000个好的 和 10 个异常数据——进行模型的微调，调整ε的值和特征的选择
  • 测试集：用2000个好的，和10个异常数据——来判断模型的泛化能力

• 方法二（当数据及其不平衡的时候使用最好）（这时是有10000个好的，2个坏的）：

  • 测试集用：6000个好的
  • 交叉验证集：用4000个好的 和 2 个异常数据——进行模型的微调，调整ε的值和特征的选择。

  缺点：不能测试模型的泛化能力，无法评估

【注释】：

? 这不是监督学习，因为没有进行数据的标记，这里的 好数据6000 和瑕疵数据 20 都是我们假设（原文是 Assume labeled）的

—— 引出了下文，那你都是认为是假设标记了,那为什么直接标记，所以为什么不使用监督学习呢？？？？

5、什么时候使用监督学习，什么时候使用异常检测

5.1 监督学习 VS 异常值检测

• 异常值检测：

  • ※※※应用于检测目标的异常值 可能是以前没有学到的，不像任何 一个训练集给出的异常值例子
  • 适合 具有 少量异常值 和 大量正常值 数据量

• 监督学习：

  • ※※※测试集中的异常值，和我们以前学习的样本有些相似之处
  • 适合 具有 大量异常值 和 大量正常值 的数据量

5.2 举一个例子

• 异常值检测的例子：

  ? 比如说电信诈骗：诈骗手法层出不穷，我们模型学习完以前的诈骗方法，但是他三天 / 几个月之后 又出现了新的咋骗手法，总是和出新的，和以前不同——这个时候就要使用**“异常值检测”**

• 监督学习的例子：

  ? 比如说 垃圾邮件检测，经历了30多年，垃圾邮件无非是那几类：钓鱼网站，推销产品，诱导消费…

  我们可以学习以前的一些例子，然后通过检测测试集的例子，总会发现有一些相似之处——这是就要使用**“监督学习”**法

6、选择使用什么样的特征

• 在监督学习中：就算我们选择了一些额外不相关的特征，我们也不受影响，因为有——特征放缩
• 在异常值检测中：对于未标记的数据，这就显得比监督学习 尤其的重要了

6.1 如何选择

【※※※核心】：

• 选择的特征 或多或少 符合 高斯分布/正态分布

• 如果要不符合高斯分布，就把他改成高斯分布

• 一些异常的数据可能也会有较高的𝑝(𝑥)值，因而被算法认为是正常的——需要进一步分析并找出特征

选择方法一：符合高斯分布的特征情况：

以特征X举例，在画布上画出X特征的分布，这里的X特征就 比较符合 “高斯分布”——这就是一个很好的候选特征

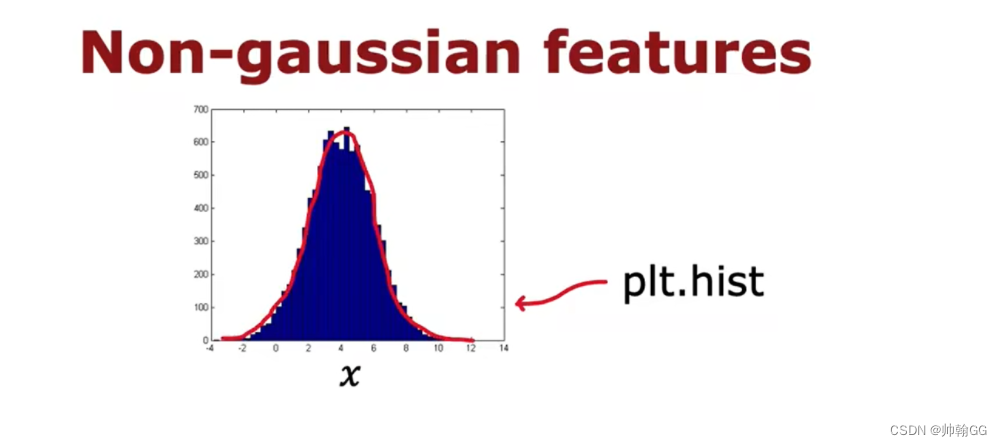
• 不符合高斯分布的特征的情况——变成符合：

  • 首先是判断，我们是否真的需要这个特征变量

  • 如果真的需要，那我们进行进一步的转变，变成符合高斯分布的特征

通过 log（x）函数 ，变成了符合正态分布的情况。

其实还有许多变化的方法：

? 常用的将数据转换成符合高斯分布的方法包括对数变换（log transformation）、平方根变换（square root transformation）、Box-Cox变换等。这些变换可以使数据更加接近正态分布的形态。

? 如果数据中存在明显的异常值，那么将其转换成符合高斯分布的形式可能会使得异常值更加明显，从而更容易被检测到。

[^]: (注：在python 中，通常用np.log1p()函数，𝑙𝑜𝑔1𝑝就是 𝑙𝑜𝑔(𝑥 + 1)，可以避免 出现负数结果，反向函数就是np.expm1())

实例实施过程：

选择方法二： 从学习不好的结果中进行进一步选择特征

【核心】：

一个常见的问题是一些异常的数据可能也会有较高的𝑝(𝑥)值，因而被算法认为是正常的。这种情况下误差分析能够帮助我们 ——我们可以分析那些被算法错误预测为正常的数据，观察能否找出一些问题。

• 正常我们选择完成 交叉验证集 验证，发现有一些数据（这里对应的X蓝色坐标点）看起来很正常（ 有较高的P（x）），但是是异常数据——怎么才能解决这个问题呢？？？

• 这时候就需要找出其他特征，根据其他特征一起来进行判断会更容易——他虽然在X1(这里指发动机 温度)的特征上表现得正常，但是在我们没有选中的X2 （这里指发动机震动频率）的特征上表现得异常。所以还需要选择特征X2，然后结合X1 X2，把X1 X2他们组合起来进行一起来判断。

? 这也是交叉验集微调的过程

6.2 举例