Lang–Kobayashi方程实现混沌python实现混沌序列图像

Lang–Kobayashi方程描述为：

第一部分（Drive laser）是描述的驱动激光器，第二部分（Response laser）描述的是响应激光器。实验结构图如下：

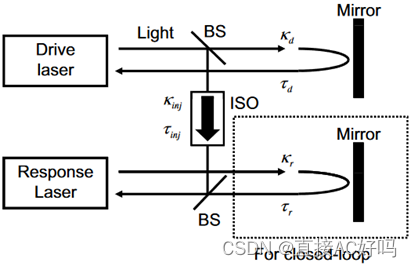
虚线框表示响应激光器中的闭环配置。开环中响应激光器无反馈，产生的时间序列与驱动激光器相同，而闭环配置对于响应激光器添加了反馈，产生的时间序列与驱动激光器不同。
开环配置产生的混沌时间序列如下：

Figure 3开环配置混沌时间序列（蓝色为驱动激光器，红色为响应激光器，黑色为延迟驱动激光）

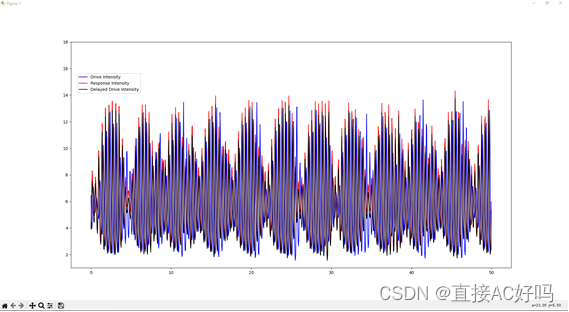
Figure 4开环配置三种混沌时间序列对比

开环配置产生的混沌时间序列如下：

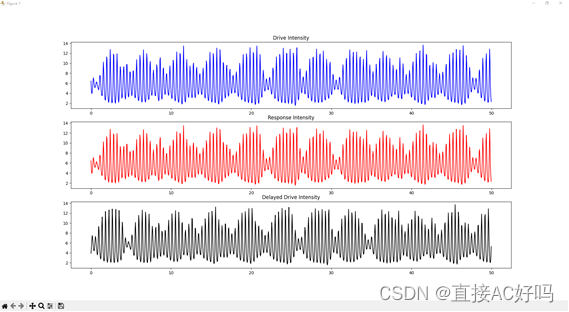
开环配置中驱动与响应和延时之间的对比：

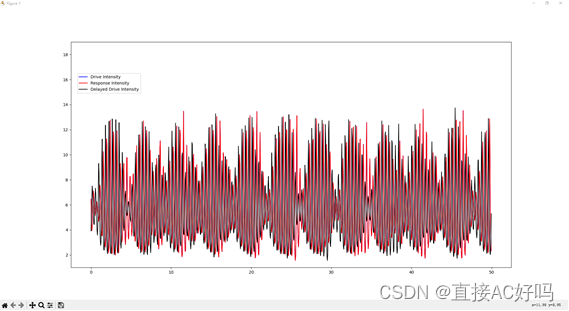
闭环配置产生的混沌时间序列：

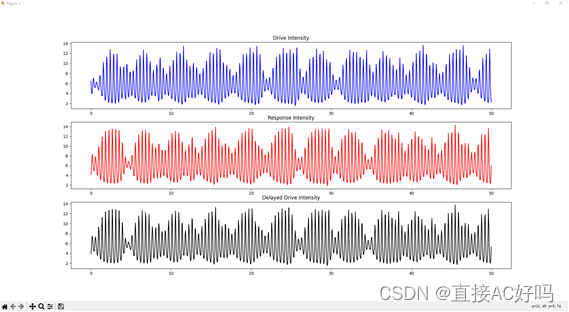
闭环配置中驱动与响应和延时之间的对比：

混沌序列的横坐标为时间序列，点与点之间的间隔为定值。纵坐标为各中电场振幅的平方。混沌与噪声十分相似，又有很大不同：混沌是指非线性动力学系统的复杂演化行为，具有确定性的规律，但对初始条件极其敏感。噪声是指随机性的信号或干扰，以无规律的、随机的成分为特征，会对信号进行干扰和扰动。混沌系统的行为是由特定方程或规则决定的，而噪声是一个随机过程。混沌系统表现出的行为是非周期性的，而噪声通常不具备明确的周期性。

闭环配置数值模拟python代码：

import math
import matplotlib.pyplot as plt
C = 2.99792458e8
M = 6
r3Dri = 0.008
r3Res = 0.008
JRatio = 1.3
LDri = 0.6
LRes = 0.6
LInj = 1.2
detun = -4.0e9
kapInjRatio = 12.5
r2 = 0.556
tauIn = 8.0e-12
lambdaa = 1.537e-6
Gn = 8.4e-13
N0 = 1.4e24
tauP = 1.927e-12
tauS = 2.04e-9
alpha = 3.0
Nth = float
Jth = float
J = float
kapDri = float
kapRes = float
kapInj = float
tauDri = float
tauRes = float
tauInj = float
omega0 = float
phaseShiftDri = float
phaseShiftRes = float
phaseShiftInj = float
DELAY_MAX = 100000
eDelayDri = [0.0]*DELAY_MAX
phiDelayDri = [0.0]*DELAY_MAX
eDelayRes = [0.0]*DELAY_MAX
phiDelayRes = [0.0]*DELAY_MAX
eDelayInj = [0.0]*DELAY_MAX
phiDelayInj = [0.0]*DELAY_MAX
delayDriNum = int
delayResNum = int
delayInjNum = int
delayDriIndex = int
delayResIndex = int
delayInjIndex = int
def calcParameter(h):
    global tauRes, tauInj, J, kapInj, kapDri, kapRes, tauDri, omega0, phaseShiftDri, phaseShiftRes, phaseShiftInj, delayResNum, delayInjNum, delayDriNum
    Nth = N0 + 1.0 / tauP / Gn
    Jth = Nth / tauS
    J = JRatio * Jth
    kapDri = (1 - r2 * r2) * r3Dri / r2 / tauIn
    kapRes = (1 - r2 * r2) * r3Res / r2 / tauIn
    kapInj = kapInjRatio * kapDri
    tauDri = 2.0 * LDri / C
    tauRes = 2.0 * LRes / C
    tauInj = LInj / C
    omega0 = 2.0 * math.pi*C/lambdaa
    phaseShiftDri = math.fmod(omega0 * tauDri, 2.0 * math.pi)
    phaseShiftRes = math.fmod((omega0 - 2.0 * math.pi * detun) * tauRes, 2.0 * math.pi)
    phaseShiftInj = math.fmod(omega0 * tauInj, 2.0 * math.pi)
    delayDriNum = int(tauDri / h)
    delayResNum = int(tauRes / h)
    delayInjNum = int(tauInj / h)

def initializeDelay(a):
    global delayDriIndex,delayInjIndex,delayResIndex,DELAY_MAX
    delayDriIndex = 0
    delayResIndex = 0
    delayInjIndex = 0
    for item in range(DELAY_MAX):
        eDelayDri[item] = a[0]
        phiDelayDri[item] = a[1]
    for item in range(DELAY_MAX):
        eDelayRes[item] = a[3]
        phiDelayRes[item] = a[4]
    for item in range(DELAY_MAX):
        eDelayInj[item] = 0.0
        phiDelayInj[item] = 0.0


def laser(x,b,theta):
    global kapRes,kapInj,kapDri,delayResIndex,delayInjIndex,delayDriIndex,J
    b[0] = 1.0 / 2.0 * (Gn * (x[2] - N0) - 1.0 / tauP) * x[0] + kapDri * eDelayDri[delayDriIndex] * math.cos(theta[0])
    b[1] = alpha / 2.0 * (Gn * (x[2] - N0) - 1.0 / tauP) - kapDri * eDelayDri[delayDriIndex]/ x[0] * math.sin(theta[0])
    b[2] = J - x[2] / tauS - Gn * (x[2] - N0) * x[0] * x[0]
    b[3] = 1.0 / 2.0 * (Gn * (x[5] - N0) - 1.0 / tauP) * x[3] + kapRes * eDelayRes[delayResIndex] * math.cos(theta[1]) + kapInj * eDelayInj[delayInjIndex] * math.cos(theta[2])
    b[4] = alpha / 2.0 * (Gn * (x[5] - N0) - 1.0 / tauP) - kapRes * eDelayRes[delayResIndex] / x[3] * math.sin(theta[1]) - kapInj * eDelayInj[delayInjIndex] / x[3] * math.sin(theta[2])
    b[5] = J - x[5] / tauS - Gn * (x[5] - N0) * x[3] * x[3]

def rungeKutta(a, h, t):
    global delayDriIndex,delayInjIndex,delayResIndex,phaseShiftRes,phaseShiftInj,phaseShiftDri
    x=[0.0]*M
    b=[[0.0]*M]*4
    theta=[0.0]*3
    theta[0] = math.fmod(phaseShiftDri + a[1] - phiDelayDri[delayDriIndex], 2.0 * math.pi)
    theta[1] = math.fmod(phaseShiftRes + a[4] - phiDelayRes[delayResIndex], 2.0 * math.pi)
    theta[2] = math.fmod(phaseShiftInj + a[4] - phiDelayInj[delayInjIndex] - 2.0 * math.pi * detun * t, 2.0 * math.pi)
    for item in range(4):
        for jtem in range(M):
            if item == 0:
                x[jtem] = a[jtem]
            if item == 1:
                x[jtem] = a[jtem] + h * b[0][jtem] / 2.0
            if item == 2:
                x[jtem] = a[jtem] + h * b[1][jtem] / 2.0
            if item == 3:
                x[jtem] = a[jtem] + h * b[2][jtem]
        laser(x, b[item], theta)
    for item in range(M):
        a[item] += h * (b[0][item] + 2.0 * b[1][item] + 2.0 * b[2][item] + b[3][item]) / 6.0
    eDelayDri[delayDriIndex] = a[0]
    eDelayRes[delayResIndex] = a[3]
    eDelayInj[delayInjIndex] = a[0]
    phiDelayDri[delayDriIndex] = a[1]
    phiDelayRes[delayResIndex] = a[4]
    phiDelayInj[delayInjIndex] = a[1]
    delayDriIndex = (delayDriIndex + 1) % delayDriNum
    delayResIndex = (delayResIndex + 1) % delayResNum
    delayInjIndex = (delayInjIndex + 1) % delayInjNum

if __name__ == "__main__":
    a = [0.0]*M
    t = float
    h = 5.0e-12
    transient = 5000.0e-9
    tMax = 50.0e-9
    trans = int(transient / h)
    n = int(tMax / h)
    div = 10
    a[0] = 1.3e10
    a[1] = 0.0
    a[2] = 1.90e24
    a[3] = 1.4e10
    a[4] = 0.0
    a[5] = 1.85e24
    initializeDelay(a)
    calcParameter(h)
    for item in range(trans):
        t = h*item
        rungeKutta(a, h, t)
        pass
    timevalue = []
    DI = []
    RI = []
    DDI = []
    for item in range(n):
        t = h*(trans + item)
        if item % div == 0:
            print(h*item*1e9, end=' ')
            timevalue.append(h*item*1e9)
            print(a[0] * a[0] * 1e-20, end=' ')
            DI.append(a[0] * a[0] * 1e-20)
            print(a[3] * a[3] * 1e-20, end=' ')
            RI.append(a[3] * a[3] * 1e-20)
            print(eDelayDri[delayDriIndex] * eDelayDri[delayDriIndex] * 1e-20)
            DDI.append(eDelayDri[delayDriIndex] * eDelayDri[delayDriIndex] * 1e-20)
        rungeKutta(a, h, t)
plt.subplot(3, 1, 1)
plt.plot(timevalue, DI, color='blue')
plt.title("Drive Intensity")
plt.subplot(3, 1, 2)
plt.plot(timevalue, RI, color='red')
plt.title("Response Intensity")
plt.subplot(3,1,3)
plt.plot(timevalue,DDI,color='black')
plt.title("Delayed Drive Intensity")
plt.show()
plt.plot(timevalue, DI, color='blue', label='Drive Intensity')
plt.plot(timevalue, RI, color='red', label='Response Intensity')
plt.plot(timevalue, DDI, color='black', label='Delayed Drive Intensity')
plt.legend(loc='upper left', bbox_to_anchor=(0.01, 0.87))
plt.ylim(1, 18)
plt.show()

开环配置数值模拟python代码：

import math
import matplotlib.pyplot as plt
C=2.99792458e8#光速
M=6#方程的数量
r3Dri=0.008#驱动器外镜反射率
JRatio=1.3#归一化注入电流
LDri=0.6#驱动器外腔长度
LInj=1.2#驱动器和相应激光器之间的距离
detun=0.0e9#光频失谐频率
kapInjRatio=1.0#注入强度比驱动反馈强度
r2=0.556#内镜反射率
tauIn=8.0e-12#内腔往返时间
lambdaa=1.537e-6#光的波长
Gn=8.4e-13#增益系数
N0=1.4e24#透明载流子密度
tauP=1.927e-12#光子寿命
tauS=2.04e-9#载体寿命
alpha=3.0#参数
DELAY_MAX=100000#延迟的最大数组大小
J=float#注入电流
kapDri=float
kapInj=float
tauDri=float
tauInj=float
delayDriNum=int
delayInjNum=int
delayDriIndex=int
delayInjIndex=int
omega0=float
phaseShiftDri=float
phaseShiftInj=float
eDelayDri=[0]*DELAY_MAX
phiDelayDri=[0]*DELAY_MAX
eDelayInj=[0]*DELAY_MAX
phiDelayInj=[0]*DELAY_MAX
def calcParameter(h):
    global J,kapInj,phaseShiftInj,phaseShiftDri,delayInjNum,delayDriNum,tauS,JRatio,kapInj,kapDri,tauInj,tauDri,omega0,kapInjRatio,lambdaa,C
    Nth = N0 + 1.0 / tauP / Gn#阈值载流子密度
    Jth = Nth / tauS#阈值注入电流
    J = JRatio * Jth#注入电流
    kapDri = (1 - r2 * r2) * r3Dri / r2 / tauIn#驱动反馈强度
    kapInj = kapInjRatio * kapDri#从驱动到响应的注射强度
    tauDri = 2.0 * LDri / C#驱动的外腔往返时间
    tauInj = LInj / C#从驱动到响应的耦合时间
    omega0 = 2.0 * math.pi * C /lambdaa#光角频率
    phaseShiftDri = math.fmod(omega0 * tauDri, 2.0 * math.pi)#驱动的初始相移
    phaseShiftInj = math.fmod(omega0 * tauInj, 2.0 * math.pi)#耦合的初始相移
    delayDriNum = int(tauDri/h)
    delayInjNum = int(tauInj/h)
def initializeDelay(a):
    global delayDriIndex,delayInjIndex,DELAY_MAX
    delayDriIndex = delayInjIndex = 0
    for item in range(DELAY_MAX):
        eDelayDri[item] = a[0]
        phiDelayDri[item] = a[1]
    for item in range(DELAY_MAX):
        eDelayInj[item] = 0.0
        phiDelayInj[item] = 0.0
        pass
    pass
def laser(x,b,theta):
    global delayDriIndex,delayInjIndex,Gn,N0,tauP,kapInj,kapDri,alpha,J,tauS
    b[0] = 1.0 / 2.0 * (Gn * (x[2] - N0) - 1.0 / tauP) * x[0] + kapDri * eDelayDri[delayDriIndex] * math.cos(theta[0])
    b[1] = alpha / 2.0 * (Gn * (x[2] - N0) - 1.0 / tauP) - kapDri * eDelayDri[delayDriIndex] / x[0] * math.sin(theta[0])
    b[2] = J - x[2] / tauS - Gn * (x[2] - N0) * x[0] * x[0];
    b[3] = 1.0 / 2.0 * (Gn * (x[5] - N0) - 1.0 / tauP) * x[3] + kapInj * eDelayInj[delayInjIndex] * math.cos(theta[1])
    b[4] = alpha / 2.0 * (Gn * (x[5] - N0) - 1.0 / tauP) - kapInj * eDelayInj[delayInjIndex] / x[3] * math.sin(theta[1])
    b[5] = J - x[5] / tauS - Gn * (x[5] - N0) * x[3] * x[3];
def rungeKutta(a,h,t):
    global delayDriIndex,delayInjIndex,M,phaseShiftDri,phaseShiftInj,detun,delayDriNum,delayInjNum
    x=[0]*M
    b=[[0]*M]*4
    theta=[0]*2
    theta[0] = math.fmod(phaseShiftDri + a[1] - phiDelayDri[delayDriIndex], 2.0 * math.pi)
    theta[1] = math.fmod(phaseShiftInj + a[4] - phiDelayInj[delayInjIndex] - 2.0 * math.pi * detun * t, 2.0 * math.pi)
    for item in range(4):
        for jtem in range(M):
            if item == 0:
                x[jtem] = a[jtem]
            if item == 1:
                x[jtem] = a[jtem] + h * b[0][jtem] / 2.0
            if item == 2:
                x[jtem] = a[jtem] + h * b[1][jtem] / 2.0
            if item == 3:
                x[jtem] = a[jtem] + h * b[2][jtem]
        laser(x, b[item], theta)
    for item in range(M):
        a[item] += h * (b[0][item] + 2.0 * b[1][item] + 2.0 * b[2][item] + b[3][item]) / 6.0
    #更新延迟数组
    eDelayDri[delayDriIndex] = a[0]
    eDelayInj[delayInjIndex] = a[0]
    phiDelayDri[delayDriIndex] = a[1]
    phiDelayInj[delayInjIndex] = a[1]
    delayDriIndex = (delayDriIndex + 1) % delayDriNum
    delayInjIndex = (delayInjIndex + 1) % delayInjNum
if __name__ == "__main__":
    a = [0] * M
    h = 5.0e-12#计算步长
    transient = 5000.0e-9#瞬态时间
    tMax = 50.0e-9#时间步长
    trans = int(transient / h)
    n = int(tMax / h)
    div = 10#绘图间隔
    a[0] = 1.3e10#驱动的电场振幅
    a[1] = 0.0#用于驱动的电场相位
    a[2] = 1.90e24#驱动载流子密度
    a[3] = 1.4e10#响应的电场振幅
    a[4] = 0.0#响应的电场相位
    a[5] = 1.85e24#响应载流子密度
    time_value=[]#时间序列
    DI=[]#驱动强度
    RI=[]#反应强度
    DDI=[]#延迟驱动强度
    initializeDelay(a)
    calcParameter(h)#过渡过程计算的数学模型
    for item in range(trans):
        t = h * item
        rungeKutta(a, h, t)
    for item in range(n):
        t = h * (trans + item)
        if item % div == 0:
            print(h * item * 1e9, end=' ')
            time_value.append(h * item * 1e9)
            print(a[0] * a[0] * 1e-20, end=' ')
            DI.append(a[0] * a[0] * 1e-20)
            print(a[3] * a[3] * 1e-20, end=' ')
            RI.append(a[3] * a[3] * 1e-20)
            print(eDelayDri[delayDriIndex] * eDelayDri[delayDriIndex] * 1e-20)
            DDI.append(eDelayDri[delayDriIndex] * eDelayDri[delayDriIndex] * 1e-20)
        rungeKutta(a, h, t)
plt.subplot(3,1,1)
plt.plot(time_value,DI,color='blue')
plt.title("Drive Intensity")
plt.subplot(3,1,2)
plt.plot(time_value,RI,color='red')
plt.title("Response Intensity")
plt.subplot(3,1,3)
plt.plot(time_value,DDI,color='black')
plt.title("Delayed Drive Intensity")
plt.show()
plt.plot(time_value,DI,color='blue',label='Drive Intensity')
plt.plot(time_value,RI,color='red',label='Response Intensity')
plt.plot(time_value,DDI,color='black',label='Delayed Drive Intensity')
plt.legend(loc='upper left', bbox_to_anchor=(0.01, 0.87))
plt.ylim(1,19)
plt.show()

运行的代码，依照光通信大书中附件的c语言代码改写成的python代码，运用的积分思想是数学中的四阶龙格库塔的方法，对于上次的模型的代码修改还在进行中。欢迎佬们对上次二阶龙格库塔解混沌方程的方法进行指导！