力扣77. 组合（java 回溯法）

Problem: 77. 组合

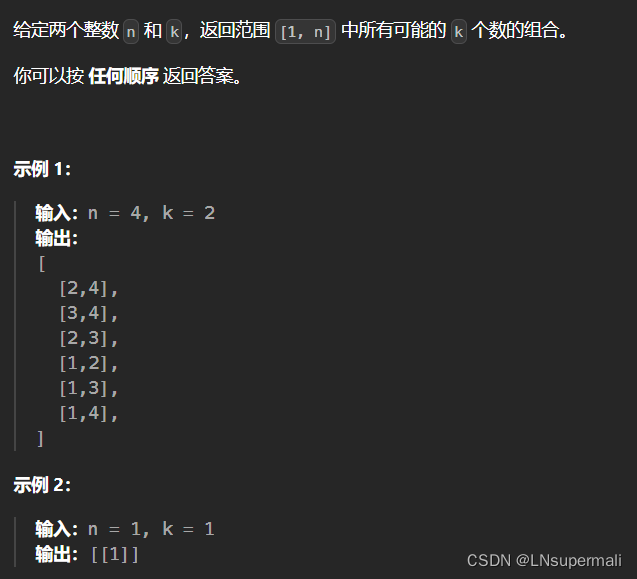
题目描述

思路

题目要求给出1-n中每k个数一组的所有组合，我们可以利用回溯，将其穷举出来，具体的：

1.以数字1-n为回溯的决策阶段，回溯的起始阶段为1
2.回溯函数的结束条件有两个：1.当决策路径的长度等于k时，将当前的路径添加到结果集合中并返回；2.当决策阶段等于k+1时返回（因为等于k+1时表示1-k阶段已经穷举完毕）
3.回溯处理（递归决策树），在每个阶段恢复上一个阶段的状态

解题方法

1.定义二维结果集result
2.调用并编写回溯函数：

2.1当决策路径的长度k时，将当前的路径添加到结果集合中并返回；.当决策阶段等于k+1时返回
2.2先不添加决策到决策路径的递归，再添加决策到决策路径的递归同时还原本决策阶段的决策状态

复杂度

时间复杂度:

$O(C_n^k)$

空间复杂度:

$O(n+C_n^k)$

Code

class Solution {
    //Save the result
    private List<List<Integer>> result = new ArrayList<>();

    /**
     * Get the combination
     * @param n The range of number(1~n)
     * @param k Specifies how many numbers are in a combination
     * @return List<List<Integer>>
     */
    public List<List<Integer>> combine(int n, int k) {
        backtrack(n, k, 1, new ArrayList<Integer>());
        return result;
    }

    /**
     * Backtracking fetch combination
     * @param n The range of number(1~n)
     * @param k Specifies how many numbers are in a combination
     * @param step Decision stage
     * @param path Decision path
     */
    public void backtrack(int n, int k, int step, List<Integer> path) {
        //End condition
        if (path.size() == k) {
            result.add(new ArrayList<>(path));
            return;
        }
        //End condition
        if (step == n + 1) {
            return;
        }
        backtrack(n, k, step + 1, path);
        path.add(step);
        backtrack(n, k, step + 1, path);
        path.remove(path.size() - 1);
    }
}