第四十三篇,点线关系
一、缘起
故事的起源是做AD的插值预瞄发现一个bug,首先放上一维线性插值的代码如下:
template <typename T>
T lerp(const T &x0, const double t0, const T &x1, const double t1,
const double t) {
if (std::abs(t1 - t0) <= 1.0e-6) {
return x0;
}
const double r = (t - t0) / (t1 - t0);
const T x = x0 + r * (x1 - x0);
return x;
}比如在两个轨迹点a和b之间做插值预瞄,正常来说插值点应当落在ab之间,一开始没发现什么问题,只是轨迹跟踪误差有点儿大,就找优化的手段。
二、现象与初步分析
找来找去最后还是通过MATLAB plot做了个动画发现了端倪,有的时段插值后的预瞄距离会莫名其妙地逐渐缩短,换句话说,插值预瞄点会逐渐靠近自车甚至飘到自车后头去。
分析后发现,当自车在线段ab之外时正常,如下面左图所示场景;当自车落在线段ab之间时问题就出现了,如下面右图所示场景(P是期望的插值位置):

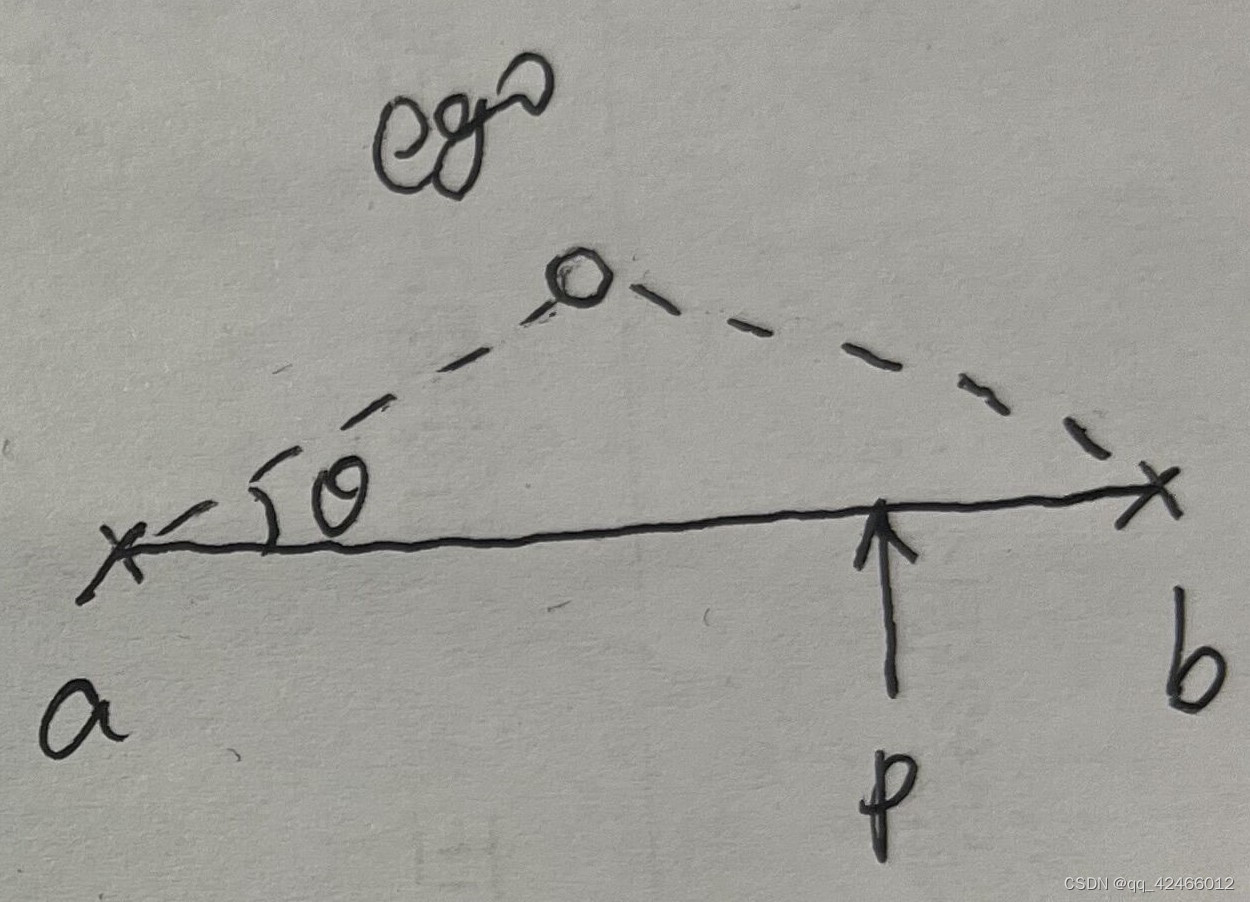
进一步分析发现,当自车落在线段ab之间时,按照插值原理,自车与后方点即a点的距离应置为负值才能保证插值结果的正确性,而代码中未做处理,执行std::hypot()之后就不管了,所以无论何种场景,与任何点的距离都是正值,这种没头脑的不符合数学物理常识的方法是有隐患的。
三、数学抽象
到这里也就明确了,需要对自车与轨迹点连线ab的相对位置做检查,并根据检查结果对自车与a点的距离做正负处理,抽象为数学问题即点线关系。
在本例中,为点在线段区间内还是区间外的问题,如下图所示:
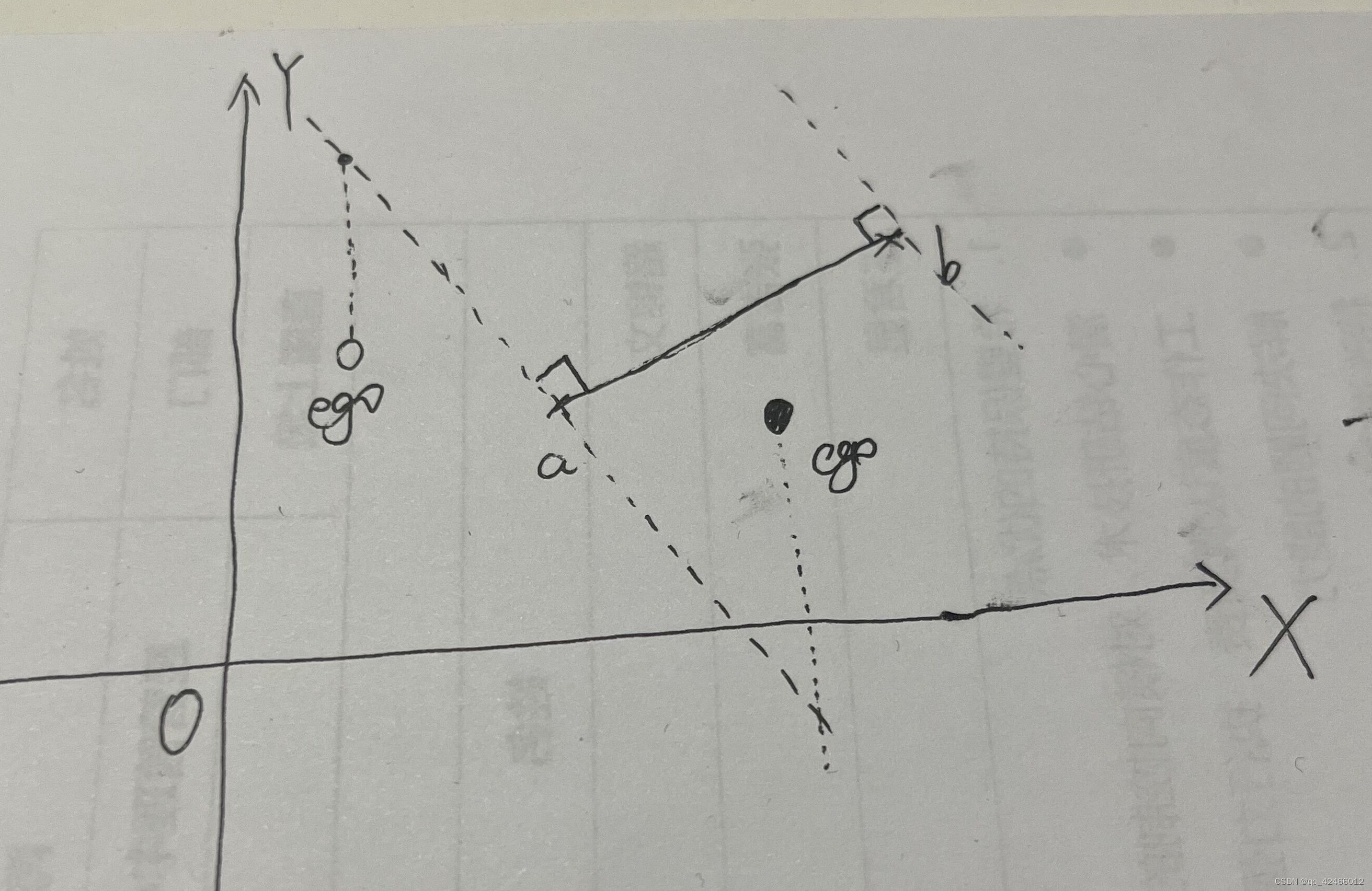
四、方法一
从几何学的角度可知,可以用构造直线方程的方法来做。
首先,我们有ab两点的坐标,很容易构造出它俩所在直线的方程y=kx+m;
然后,经过点a且与线ab垂直的直线Line1、经过点b且与线ab垂直的直线Line2,Line1与Line2所夹形成一个空间,如果自车在此空间外,则与a点的距离为正;如果自车落在此空间内部,则需将与a点的距离置为负;
根据初中数学,很容易可知Line1与Line2的斜率都为-1/k,它们分别经过点a、b,则可以得出完整的直线方程;
关键来了,Line1与Line2的直线方程有了,怎么利用这些信息检查自车是否在区间内?
方法是这样的:将自车坐标的x代入Line1方程,得到位于Line1上的一个y,如果此y大于点a的y则自车在区间外,否则自车在区间内,查看上述示意图可知,代码如下。
double dfDistWith_a = 1; // 假定先前已算出自车与a点的距离绝对值为1m
double dfX, dfY; // 假定自车坐标
double dfX_a, dfY_a; // 假定轨迹点a的坐标
double dfX_b, dfY_b; // 假定轨迹点b的坐标
if (std::abs(dfX_a-dfX_b) > 1E-4)
{
// 这里的处理直接取了倒数,省去一步检查除数为0的操作
double k_perpendicular = (dfY_b-dfY_a) / (dfX_b-dfX_a);
k_perpendicular *= -1.0; // x = k*y + b
double b_perpendicular_a = dfX_a - k_perpendicular * dfY_a;
double b_perpendicular_b = dfX_b - k_perpendicular * dfY_b;
double pseudo_x_a = k_perpendicular * dfY + b_perpendicular_a;
double pseudo_x_b = k_perpendicular * dfY + b_perpendicular_b;
if ((dfX>pseudo_x_a && dfX<pseudo_x_b) ||
(dfX<pseudo_x_a && dfX>pseudo_x_b))
{
dfDistWith_a *= -1.0F;
}
}
else
{
if ((dfY>dfY_a && dfY<dfY_b) ||
(dfY<dfY_a && dfY>dfY_b))
{
dfDistWith_a *= -1.0F;
}
}五、更优解
另外,还有一个更简便代码量也更少的方法,即向量夹角法。
重新观察最上面的左右两个图可以发现这样一个规律,当自车在区间外时,自车与a点所成向量,与向量ab的夹角为钝角,否则为直角或锐角。
有了这一信息,可以想到,将上述两个向量构造出来,做向量点乘(也叫内积),判断点乘结果的正负(钝角为负,否则为0或正),即可得知自车与a点的距离该正还是该负,方便快捷!
代码如下,代码量和逻辑都简洁了很多,并且少了除法、ab是横线竖线等特殊情况的判断,优雅!
如果使用二维向量库Vec2d的话代码量会更少。
double dfDistWith_a = 1; // 假定先前已算出自车与a点的距离绝对值为1m
double dfX, dfY; // 假定自车坐标
double dfX_a, dfY_a; // 假定轨迹点a的坐标
double dfX_b, dfY_b; // 假定轨迹点b的坐标
double dfVector_a_x = dfX - dfX_a; // 构造一个向量
double dfVector_a_y = dfY - dfY_a;
double dfVector_b_x = dfX_b - dfX_a; // 构造另一个向量
double dfVector_b_y = dfY_b - dfY_a;
if (dfVector_a_x*dfVector_b_x + dfVector_a_y*dfVector_b_y > 0) // 向量点乘
{
dfDistWith_a *= -1.0F; // over
}本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!