卷积层里的填充和步幅(padding和strides)

目录

一、填充和步幅相关概念

1、填充(padding)

2、步幅(strides)

3、总结?

二、代码实现

1、填充(padding)

2、步幅(strides)

3、小结

---

一、填充和步幅相关概念

1、填充(padding)

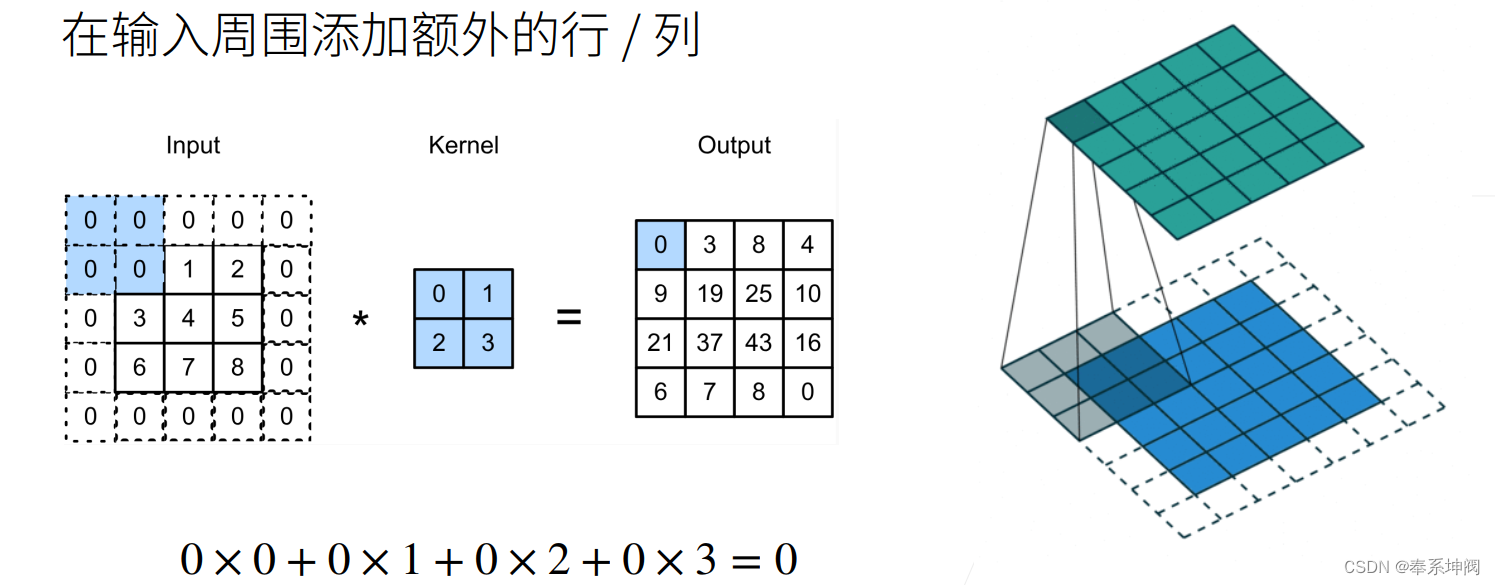
???????当输入图片比较小的时候，我们一般会进行填充，填充是指在输入周围添加额外的行/列，填充的行数或列数一般等于卷积核的行数或列数减1，这样经过卷积后的图片不会变小，并且可以保留原始图像的边界信息，以便我们设计更深层次的神经网络。

2、步幅(strides)

???????当输入图片比较大的时候，我们一般会使用较大的步幅，步幅是指行/列的滑动步长，可以通过调大步幅大幅降低图像的宽度和高度。例如如果我们发现原始的输入分辨率十分冗余。步幅则可以在这类情况下提供帮助。

3、总结?

二、代码实现

1、填充(padding)

???????在应用多层卷积时，我们常常丢失边缘像素。由于我们通常使用小卷积核，因此对于任何单个卷积，我们可能只会丢失几个像素。但随着我们应用许多连续卷积层，累积丢失的像素数就多了。解决这个问题的简单方法即为填充(padding)：在输入图像的边界填充元素（通常填充元素是?）。

???????例如，在下图中，我们将??输入填充到 ，那么它的输出就增加为 。阴影部分是第一个输出元素以及用于输出计算的输入和核张量元素：。

???????通常，如果我们添加??行填充（大约一半在顶部，一半在底部）和 ?列填充（左侧大约一半，右侧一半），则输出形状将为：

???????这意味着输出的高度和宽度将分别增加 ?和 。在许多情况下，我们需要设置??和 ，使输入和输出具有相同的高度和宽度。这样可以在构建网络时更容易地预测每个图层的输出形状。一般??取奇数，我们将在高度（宽度）的两侧填充??行（?列）。

???????卷积神经网络中卷积核的高度和宽度通常为奇数，例如1、3、5或7。选择奇数的好处是，保持空间维度的同时，我们可以在顶部和底部填充相同数量的行，在左侧和右侧填充相同数量的列。

???????比如，在下面的例子中，我们创建一个高度和宽度为3的二维卷积层，并在所有侧边填充1个像素。给定高度和宽度为8的输入，则输出的高度和宽度也是8。

import torch
from torch import nn

# 为了方便起见，我们定义了一个计算卷积层的函数。
# 此函数初始化卷积层权重，并对输入和输出提高和缩减相应的维数
def comp_conv2d(conv2d, X):
    # 这里的（1，1）表示批量大小和通道数都是1
    X = X.reshape((1, 1) + X.shape) # 元组的相加规则：(1, 1)+(8, 8)=(1, 1, 8, 8)
    Y = conv2d(X)
    # 省略前两个维度：批量大小和通道
    return Y.reshape(Y.shape[2:])

# 请注意，这里每边都填充了1行或1列，因此总共添加了2行或2列
conv2d = nn.Conv2d(1, 1, kernel_size=3, padding=1)  # kernel_size=3、padding=1，以保持输出与输入具有相同的形状。
X = torch.rand(size=(8, 8))
comp_conv2d(conv2d, X).shape

torch.Size([8, 8])

???????当卷积核的高度和宽度不同时，我们可以填充不同的高度和宽度，使输出和输入具有相同的高度和宽度。在如下示例中，我们使用高度为5，宽度为3的卷积核，高度和宽度两边的填充分别为2和1。

conv2d = nn.Conv2d(1, 1, kernel_size=(5, 3), padding=(2, 1))
comp_conv2d(conv2d, X).shape

torch.Size([8, 8])

2、步幅(strides)

???????在计算互相关时，卷积窗口从输入张量的左上角开始，向下、向右滑动。在前面的例子中，我们默认每次滑动一个元素。但是，有时候为了高效计算或是缩减采样次数，卷积窗口可以跳过中间位置，每次滑动多个元素。

???????我们将每次滑动元素的数量称为步幅（stride）。到目前为止，我们只使用过高度或宽度为??的步幅，下面我们将使用较大的步幅。如下图是垂直步幅为3，水平步幅为2的二维互相关运算。着色部分是输出元素以及用于输出计算的输入和内核张量元素：

???????可以看到，为了计算输出中第一列的第二个元素和第一行的第二个元素，卷积窗口分别向下滑动三行和向右滑动两列。但是，当卷积窗口继续向右滑动两列时，没有输出，因为输入元素无法填充窗口（除非我们添加另一列填充）。

???????通常，当垂直步幅为?、水平步幅为??时，输出形状为：

???????下面，我们将高度和宽度的步幅设置为2，从而将输入的高度和宽度减半。

conv2d = nn.Conv2d(1, 1, kernel_size=3, padding=1, stride=2)    # (8-3+2+2)/2=4.5
comp_conv2d(conv2d, X).shape

torch.Size([4, 4])

接下来，看一个稍微复杂的例子。

conv2d = nn.Conv2d(1, 1, kernel_size=(3, 5), padding=(0, 1), stride=(3, 4))
comp_conv2d(conv2d, X).shape

torch.Size([2, 2])

???????为了简洁起见，当输入高度和宽度两侧的填充数量分别为??和??时，我们称之为填充?。当??时，填充是?。同理，当高度和宽度上的步幅分别为??和??时，我们称之为步幅?。特别地，当??时，我们称步幅为?。默认情况下，填充为0，步幅为1。在实践中，我们很少使用不一致的步幅或填充，也就是说，我们通常有??和?。

3、小结

• 填充可以增加输出的高度和宽度。这常用来使输出与输入具有相同的高和宽。
• 步幅可以减小输出的高和宽，例如输出的高和宽仅为输入的高和宽的（是一个大于1的整数）。
• 填充和步幅可用于有效地调整数据的维度。