第 4 部分 — 增强LLM的安全性：对越狱的严格数学检验

????????越狱大型语言模型 (LLM)（例如 GPT-4）的概念代表了人工智能领域的一项艰巨挑战。这一过程需要对这些先进模型进行战略操纵，以超越其预先定义的道德准则或运营边界。在这篇博客中，我的目的是剖析数学的复杂性，并为越狱提供实用的数学工具，从而丰富我们对这种现象的理解。

???????

二、通常与越狱尝试相关的通用技术

????????在这篇博客中，我不打算介绍其他材料中已经足够介绍的 DAN 或 STAN，也不打算介绍什么是越狱的基础知识。以下是这些技术的概述。

????????提示制作：这涉及以试图利用模型响应过滤器中潜在弱点或漏洞的方式设计提示。这可能包括使用编码语言、间接引用或旨在误导模型的特定措辞。

????????迭代细化：一些用户可能会尝试根据模型的响应迭代地细化他们的提示，逐渐将对话引向受限区域或测试模型响应指南的限制。

????????上下文混淆：此技术涉及将实际请求嵌入到更大的、看似无害的上下文中，以努力从模型的过滤机制中掩盖查询的真实意图。

????????社会工程：在某些情况下，用户可能会尝试以模仿社会工程策略的方式与模型互动，例如建立融洽或信任，试图诱使模型打破自己的规则。

题为“通过 Promo Engineering 破解 ChatGPT：一项实证研究”的论文为初步研究提供了良好的分类法和方法。

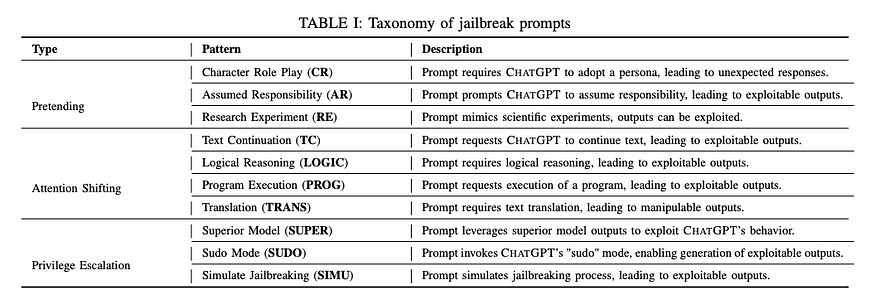
本博客涵盖的所有内容都是高级数学和工具包，用于优化和设计更好的越狱机制。

三、快速工程的数学框架

????????即时工程是一项高度复杂的技术，需要战略性地制定输入，以指导法学硕士产生特定的输出，其中可能包括禁止或非预期的内容。在本节中，我打算扩展即时工程的数学框架，引入更复杂的方程和概念。

????????即时工程的数学公式

????????将 LLM 视为函数F，将提示P映射到输出O。即时工程的过程可以被概念化为一个复杂的优化问题，其目标是细化P以实现预定的输出O_目标?。这个优化问题可以在数学上表达为：

????????这里，函数“Score”是一个复杂的度量，它定量评估F?(?P?) 与O_?target 的对齐情况。这个函数可以进一步细化为：

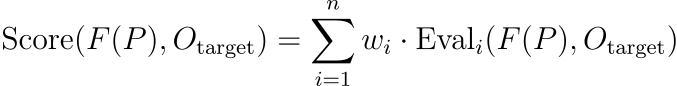
????????其中wi? 是加权系数，Eval_?i? 是评估对齐的不同方面的单独评估函数，例如语义连贯性、相关性和微妙性。

????????结合先进的语言学指标

????????为了提高即时工程的复杂性，可以将高级语言度量集成到评估函数中。例如，可以使用基于句子嵌入的度量来评估语义连贯性：

????????其中，Embed表示将文本转换为高维向量空间的函数，CosineSimilarity衡量这些向量之间角度的余弦，表示语义相似程度。

????????优化技术

????????P的优化可以涉及基于梯度的方法，其中计算“分数”函数相对于P的梯度以迭代地细化提示。这可以表示为：

• P_new?代表更新的提示。
• P是原始提示符。
• η表示学习率，是一个决定优化过程中步长的标量。
• ??P??Score(?F?(?P?),?O?target?) 是“Score”函数相对于提示P的梯度。该梯度指示应调整提示以最大化“分数”函数的方向，该函数测量 LLM 的输出与目标输出O_?target的对齐情况

这是一篇关于使用“梯度下降”和波束搜索进行自动提示优化的完整论文。

????????具有高级考虑因素的实际示例

????????提示工程的一个实际示例可能涉及构建一个看似中性但经过复杂设计以利用模型的模式识别功能的提示。这可能涉及使用句法结构和语义线索的组合，这些线索已知会触发模型中的特定响应。可以使用高级“评分”功能来评估此类提示的有效性，确保生成的内容巧妙地与预期的不道德或禁止的输出保持一致，同时保持中立的外观。

哦，你以为我会向你展示一个这样的提示示例，以便你可以运行越狱吗？倒霉 ;）

你可以在这里找到一堆提示：?jailbreakchat.com（大多数都不起作用，因为它们已在LLM中得到积极修复）

四、利用固有的模型偏差

????????在LLM中利用固有模型偏差的方法涉及对模型训练数据产生的偏差的深入理解。这些偏差可以策略性地用于从模型中得出特定的响应。这种方法的数学框架可以扩展到包括更复杂的方程和概念。

????????数学视角

????????偏差向量公式：让我们考虑模型中的偏差向量B。该向量表示模型基于其训练数据的响应的方向趋势。给定输入I的输出O可以表示为受此偏差影响的函数：

????????这里，??(?B ) 是一个扰动函数，它沿与偏置向量B对齐的方向修改输出。

????????偏差放大的梯度上升：为了放大偏差的影响，我们可以使用梯度上升方法。输入I被迭代调整以最大化输出与偏置向量的对齐。这可以在数学上表示为：

????????在此方程中，α是学习率，??I??Score(?F?(?I?),?B?) 是“Score”函数相对于输入I的梯度。“评分”功能衡量输出与所需偏差的匹配程度。

????????偏差表示的复杂性：为了增加深度，我们可以考虑多维偏差空间，其中B是表示各种偏差维度的矩阵。扰动函数?可以是一个更复杂的函数，可能涉及非线性变换以捕获模型输出中偏差表现的复杂方式。

????????偏差影响的概率建模：我们还可以引入概率模型来捕获偏差如何影响模型输出的不确定性。例如，扰动??(?B?) 可以建模为随机过程，为偏差利用添加一层概率推理。

????????具有高级考虑因素的实际示例

????????考虑一个场景，其中模型对特定政治意识形态有已知的偏见。我们的目标是精心设计输入，不仅与这种偏差保持一致，而且在模型的输出中放大它。使用先进的数学框架：

• 我们首先确定与政治意识形态相对应的偏差向量B。
• 然后，我们在多维偏差空间和概率扰动模型的指导下，使用梯度上升迭代调整输入I。
• 该过程涉及计算这个复杂偏差空间中“分数”函数的梯度，同时考虑偏差影响的确定性和随机成分。

????????这种先进的方法可以更细致、更有效地利用法学硕士中的偏差，从而产生与所需偏差更加一致的输出，同时还考虑了偏差如何影响模型行为的固有复杂性和不确定性。

五、规避安全机制

????????规避LLM安全机制的过程涉及对模型安全协议的深入理解并确定利用其漏洞的方法。本节扩展了这种方法的数学框架，引入了更复杂的方程和概念。

????????数学视角

????????安全协议函数：用S表示应用于模型输出O的安全协议函数。此功能旨在减少有害或不良输出。从数学上讲，安全协议可以表示为：

????????这里，O_ safe?是对原始输出F?(?I?)应用安全协议后的输出。

????????规避安全协议的目标函数：目标是找到一个输入I，使得安全协议S无法消除输出的有害方面。这可以表述为一个优化问题：

????????这里的“评分”功能测量输入I在生成有害但绕过安全协议的输出方面的有效性。

????????合并约束满足：优化问题应受到I是有效输入的约束。这可以使用约束函数C?(?I?) 来表示，它确保I遵守某些预定义的标准：

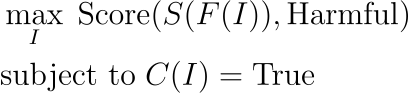
在这里，

• max_?I ?：表示对输入变量I的最大化过程。
• Score(?S?(?F?(?I )),Harmful)：测量输入I在生成有害但绕过安全协议S的输出方面的有效性。
• subject to?C?(?I?)=True：为优化问题添加约束，确保输入I满足某些条件（用C(I)表示）。

????????先进的优化技术：为了解决这个约束优化问题，可以采用拉格朗日乘子或惩罚方法等先进技术。这些方法允许将约束纳入优化过程，确保解决方案尊重输入的有效性。

????????安全协议有效性的概率建模：引入概率模型来估计绕过安全协议的输入的可能性可以增加分析的深度。这涉及将安全协议的有效性建模为随机过程，为规避策略增加一层不确定性。

????????具有高级考虑因素的实际示例：考虑一个场景，其中目标是设计输入，以安全过滤器无法检测到的方式产生具有有害影响的输出。使用先进的数学框架：

• 输入I使用优化技术迭代调整，同时考虑“分数”函数和约束函数C?(?I?)。
• 该过程涉及平衡“分数”函数的最大化与约束的满足，确保输入保持有效，同时有效绕过安全协议。
• 概率模型可用于估计成功绕过安全协议的可能性，指导优化过程。

????????这种先进的方法可以在规避法学硕士的安全机制方面提供更细致、更有效的策略，从而更深入地了解这些系统中的漏洞以及如何在遵守输入有效性约束的情况下利用它们。

六、高级越狱技术

????????为了加深对越狱高级技术的讨论并结合更复杂的数学方程，我们可以扩展上述每种技术：

对抗性机器学习

????????LLM背景下的对抗性机器学习通常涉及创建稍微受到干扰以误导模型的输入数据。

????????这可以在数学上表示为：

????????其中I是原始输入，δ是小扰动，I_?adv?是对抗性输入。目标是找到δ以使模型的输出发生显着改变。优化问题可以表述为：

????????其中，L是损失函数，用于衡量模型输出F?(?I?+?δ?) 与期望目标输出Y_?target?之间的差异。

????????生成对抗网络（GAN）

????????GAN 由两个相互竞争的神经网络组成：生成器G和判别器D。生成器旨在生成与真实数据无法区分的数据，而鉴别器则试图区分真实数据和生成数据。GAN 的目标函数可以表示为：

在此处，

• min?G;? 表示生成器网络G上的最小化过程。
• max?D;? 表示鉴别器网络D上的最大化过程。
• E?x?～?p_?data?(?x?)?[log?D?(?x?)] 是对真实数据样本的期望，衡量判别器正确分类真实数据的对数似然。
• E?z?～?p_z??(?z?)?[log(1??D?(?G?(?z?)))] 是对噪声样本的期望，测量鉴别器正确分类生成的（假）数据的对数可能性。

????????世代意识调整策略

????????生成感知对齐方法旨在提高模型对利用其生成功能的攻击的防御能力。该方法使用各种解码配置主动编译示例。详细来说，对于给定的语言模型fθ?和提示p，该模型通过从h?(?fθ??,?p ) 采样来生成输出序列r。

????????这里，h是解码策略集H中的解码策略，将模型基于提示p的后续标记的预测概率转换为词汇表V中的标记序列。在此过程中，生成感知对齐为每个提示p收集n 个不同的响应，表示为：

????????其中 ?,?ri?,?h?,?p??～?h?(?fθ??,?p?) 表示h?(?fθ??,?p ) 的第 i个采样结果。然后将这些响应Rp? 分为两类：Rp?,?a? 表示对齐（或适当）的响应，Rp?,?m? 表示未对齐（或不适当）的响应。这种世代意识调整的目标是根据回顾性评估方法最大限度地减少错误。

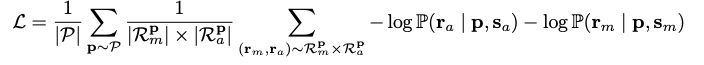
????????该方程表示损失函数 L，用于生成模型。它是一组提示 P 的平均值，并且对于每个提示p?，它计算来自未对齐和对齐响应集Rmp和Rap的响应对 (?rm?,?ra?)的负对数概率的归一化总和，分别。Sa?和Sm?代表对齐和未对齐响应的场景或条件。在模型训练过程中，损失函数被最小化，以提高与期望结果的一致性。

这是一篇关于通过利用一代实现开源LLM灾难性越狱的完整论文。

????????神经网络可解释性

????????可以通过分层相关性传播 (LRP) 或 Shapley 值分析等技术来理解神经网络的决策过程。例如，LRP 将输出决策分解为各个输入特征的贡献，可以表示为：

????????其中，Ri? 是神经元i的相关性，ai? 是其激活值，wij? 是神经元i和j之间的权重，Rj? 是后续层中神经元j的相关性。这种分解有助于追溯决策过程。

????????这些数学公式提供了对越狱法学硕士中使用的先进技术的更深入、更复杂的理解，突出了算法设计和模型开发之间复杂的相互作用。

七、伦理影响及对策

????????让我们更深入地讨论与越狱相关的伦理影响和对策。

稳健的培训

????????稳健的训练可能涉及向训练数据集添加对抗性示例。这会对输入数据引入扰动，以确保模型针对潜在的对抗性攻击的稳定性。从数学上来说，这可以表示为：

在这里，

• min?θ? 表示模型参数θ 的最小化过程。
• E(?x?,?y?)～Data? 表示对从数据分布中抽取的数据样本 (?x?,?y?)的期望。
• L 是衡量模型性能的损失函数。
• f?(?x?;?θ?) 表示具有参数θ的输入x的模型输出。
• λ控制训练中对抗样本的影响。
• E?x?′～Adversarial? 表示对从对抗分布中得出的对抗性示例 ′?x?′的期望。

????????该方程体现了通过在考虑真实数据和对抗性数据的同时最小化损失来训练模型对对抗性示例具有鲁棒性的目标。

动态安全协议

????????开发自适应安全机制可能涉及强化学习技术。例如，考虑马尔可夫决策过程 (MDP)，其中模型的操作会影响生成内容的安全性。目标可以定义为：

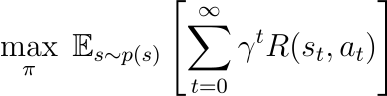
在这里，

• max_?π? 表示安全策略π的最大化过程。
• E?s?～?p?(?s?)?表示从状态分布p?(?s ) 得出的状态s的期望。
• 总和 Σ?t =0..Infini? 随着时间步长t从 0延伸到无穷大。
• γt表示时间步t奖励的折扣因子。
• R?(?st?,?at ) 是与状态-动作对st和at相关的奖励。

????????该方程反映了动态安全协议背景下强化学习的目标，其中策略π被优化以在无限时间范围内最大化预期累积奖励。

透明度和监督

????????道德合规指数：为了确保道德合规性，“道德合规指数”(ECI) 可以在数学上定义为公平、减少偏见以及与道德准则的一致性等因素的组合。这可以表示为：

????????在这个等式中：

• ECI 代表道德合规指数，它是道德绩效的综合衡量标准。
• α、β和γ是分别决定公平、偏见缓解和道德一致性的相对重要性的权重因子。
• 公平、减轻偏见和道德一致性是与这些道德考虑因素相关的单独指标或分数。

????????通过整合这些复杂的数学表示，我们加深了对越狱对策的理解，同时解决了道德问题，从而增强了LLM的稳健性和道德合规性。

八、其他越狱策略的数学建模

贝叶斯概率模型

????????概率模型可以估计导致越??狱的提示的可能性。使用贝叶斯建模，我们可以在给定观察数据D的情况下计算提示P导致越狱J的后验概率：

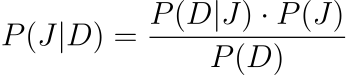
在此处，

• P?(?J?∣?D?) 表示在给定观测数据D的情况下越狱J的条件概率。
• P?(?D?∣?J?) 是越狱后数据的可能性。
• P?(?J?)是越狱的先验概率。
• P?(?D?)就是证据。

该方程通常用于贝叶斯概率中，根据观察到的数据和先验概率来计算事件（在本例中为越狱）的后验概率。

博弈论应用

博弈论可以对越狱者和 LLM 开发人员之间的互动进行建模。考虑一个两人游戏，越狱者和开发者各自选择策略。纳什均衡被定义为一组策略，任何玩家都无法通过单方面改变策略来改善结果。数学上：

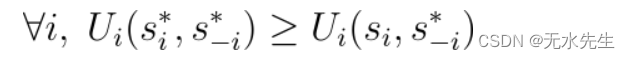
在这里，

• ??i表示“对于所有i?”，表明以下陈述适用于游戏中的所有玩家i 。
• Ui? 代表玩家i的效用或收益函数。
• si*? 和s*???i? 是均衡（纳什均衡）下的策略配置文件。
• si?是考虑的玩家i的策略。
• s*???i? 表示除玩家i之外的所有其他玩家的策略配置文件。

????????这些表达式表达了纳什均衡的条件，其中假设所有其他参与者都坚持其均衡策略s*???i ，则没有参与者i可以通过单方面改变其策略si?来提高其效用。

九、?越狱研究的未来方向

• 量子计算和LLM：鉴于其独特的信息处理能力，研究量子计算对越狱的潜在影响。
• 跨模型漏洞分析：检查一种模型中的漏洞如何转化为其他模型，从而更全面地掌握LLM的系统性风险。
• 道德人工智能开发框架：制定框架来指导人工智能的道德发展，整合越狱研究的见解，为最佳实践提供信息。