Flash Attention(1):背景介绍,与传统Attention对比,前向反向算法解析
0 英文缩写
- FA: Flash Attention
- HBM:High Bandwidth Memory,高带宽显存
0 论文
[2205.14135] FlashAttention: Fast and Memory-Efficient Exact Attention with IO-Awareness
中文:FlashAttention:一种具有 IO 感知,且兼具快速、内存高效的新型注意力算法
科研团队:斯坦福大学计算机系+纽约州立大学布法罗分校
发表时间:20220527
1 背景:
- 背景1:应用广泛:Transformer 模型在图像分类、自然语言处理等分支领域中逐渐成为最为常见的架构
- 背景2:模型扩展:随着技术不断进步,Transformer 模型在尺寸和深度等方面都进一步拓展
- 背景3:算法复杂度特征:核心模块自注意力机制(self attention)的时间复杂度和存储复杂度,均与输入长度(一般即为处理的序列长度)的平方成正比
结合背景123,可以发现更大的模型在更长的上下文背景上还存在着一定的挑战。
-
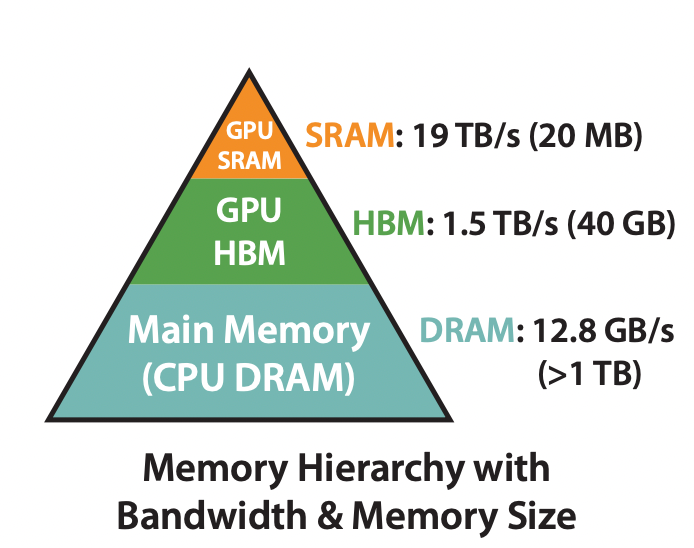
背景4:计算读写开销:论文GPU内不同存储系统的速度举例如下:
- GPU SRAM 读写(I/O)速度19 TB/s
- GPU HBM 读写(I/O)速度 1.5 TB/s
2 相关方案
在此背景之下,有人提出一些近似自注意力的方法,旨在减少注意力计算和内存需求。
- 稀疏近似
- 低秩近似
- 它们的组合
缺点:尽管这些方法可以将计算降低到线性或接近线性,但它们过于关注降低每秒所执行的浮点运算次数(FLops),换句话说更倾向于单纯降低计算复杂度。忽略来自内存访问(IO)的开销。不能实现更高且更有实用价值的计算加速范式。
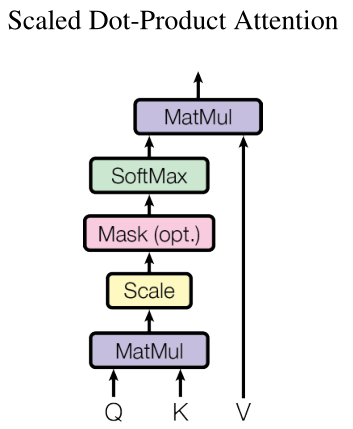
3 传统Attention
(更详细的推导过程和描述可以参考前文)
Attention机制其核心为计算输入向量的相关程度,例如在翻译过程中,不同的英文对中文的依赖程度不同,Attention机制通常可以进行如下描述
3.1 输入输出定义
- 输入1: Q Q Q 序列(query),其中 { Q = ( q 1 q 2 q 3 ? q m ) ? d k } m ∈ R m × d k , q i ∈ R 1 × d k ∣ i ∈ 1 , 2 , … , m } \left\{Q=\underbrace{\left(\begin{array}{c}q_1 \\ q_2 \\ q_3 \\ \vdots \\ q_m \end{array}\right)}_{d_{k}}\} m \in\mathbb{R}^{m\times d_k}, q_{i}\in\mathbb{R}^{1\times d_k} \mid i\in 1,2, \ldots, m\right\} ? ? ??Q=dk? ?q1?q2?q3??qm?? ???}m∈Rm×dk?,qi?∈R1×dk?∣i∈1,2,…,m? ? ??
- 输入2: K K K 序列 (key),其中 { K = ( k 1 k 2 k 3 ? k m ) ? d k } m ∈ R m × d k , k i ∈ R 1 × d k ∣ i = 1 , 2 , … , m } \left\{K=\underbrace{\left(\begin{array}{c}k_1 \\ k_2 \\ k_3 \\ \vdots \\ k_m\end{array}\right)}_{d_{k}}\} m\in\mathbb{R}^{m\times d_k}, k_{i}\in \mathbb{R}^{1\times d_k} \mid i=1,2, \ldots, m\right\} ? ? ??K=dk? ?k1?k2?k3??km?? ???}m∈Rm×dk?,ki?∈R1×dk?∣i=1,2,…,m? ? ??
- 输入3: V V V 序列 (value) ,其中 { V = ( v 1 v 2 v 3 ? v m ) ? d v } m ∈ R m × d v , v i ∈ R 1 × d v ∣ i = 1 , 2 , … , m } \left\{V=\underbrace{\left(\begin{array}{c}v_1 \\ v_2 \\ v_3 \\ \vdots \\ v_m\end{array}\right)}_{d_{v}}\} m\in\mathbb{R}^{m\times d_v}, v_{i}\in \mathbb{R}^{1\times d_v} \mid i=1,2, \ldots, m\right\} ? ? ??V=dv? ?v1?v2?v3??vm?? ???}m∈Rm×dv?,vi?∈R1×dv?∣i=1,2,…,m? ? ??
- 输出为$\text { Attention }(Q, K, V) $ 向量,计算公式:
?Attention? ( Q , K , V ) ∈ R m × d v = softmax ? ( Q K T d k ) V \text { Attention }(Q, K, V) \in\mathbb R^{m \times d_{v}}=\operatorname{softmax}\left(\frac{Q K^{T}}{\sqrt{d_{k}}}\right) V ?Attention?(Q,K,V)∈Rm×dv?=softmax(dk??QKT?)V
3.2 算法解析
第一步:矩阵乘法
为什么可以计算得到不同输入向量之间的得分
矩阵乘法
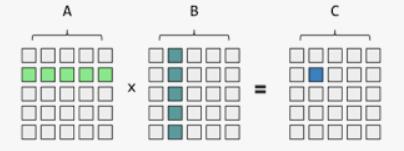
假设共有十个输入向量,每个向量的长度为512,也即为 m = 10 m=10 m=10, d k = 512 d_k=512 dk?=512
Q = ( q 1 [ 0 ] ? q 1 [ d k ] ? ? ? q 10 [ 0 ] ? q 10 [ 511 ] ) = ( q 1 ? ? q 10 ? ) Q=\left(\begin{array}{ccc} q_{1}[0] & \cdots & q_{1}[d_k] \\ \vdots & \cdots & \vdots \\ q_{10}[0] & \cdots & q_{10}[511] \end{array}\right) = \left(\begin{array}{c}\vec{q_{1}}\\\vdots\\ \vec{q_{10}} \end{array}\right) Q= ?q1?[0]?q10?[0]?????q1?[dk?]?q10?[511]? ?= ?q1???q10??? ?
K = ( k 1 [ 0 ] ? k 1 [ 511 ] ? ? ? k 10 [ 0 ] ? k 10 [ 511 ] ) = ( k 1 ? ? k 10 ? ) K=\left(\begin{array}{ccc}k_{1}[0] & \cdots & k_{1}[511] \\\vdots & \cdots & \vdots \\k_{10}[0] & \cdots & k_{10}[511]\end{array}\right) = \left(\begin{array}{c}\vec{k_{1}}\\\vdots\\ \vec{k_{10}} \end{array}\right) K= ?k1?[0]?k10?[0]?????k1?[511]?k10?[511]? ?= ?k1???k10??? ?
相乘结果如下
Q
?
K
T
∈
R
m
×
m
=
(
q
1
?
?
q
10
?
)
?
(
k
1
?
T
?
k
10
?
T
)
(
q
1
?
?
k
1
?
T
?
q
1
?
?
k
10
?
T
?
?
?
q
10
?
?
k
1
?
T
?
q
10
?
?
k
10
?
T
)
=
(
s
1
?
1
?
s
1
?
10
?
?
?
s
10
?
1
?
s
10
?
10
)
Q \cdot K^T \in \mathbf{R}^{m\times m}= \left(\begin{array}{c}\vec{q_{1}}\\\vdots\\ \vec{q_{10}} \end{array}\right) \cdot \left(\vec{k_{1}}^T\cdots \vec{k_{10}}^T\right) \left(\begin{array}{ccc} \vec{q_{1}}\cdot\vec{k_{1}}^T & \cdots & \vec{q_{1}}\cdot\vec{k_{10}}^T \\\vdots & \cdots & \vdots \\\vec{q_{10}}\cdot\vec{k_{1}}^T& \cdots & \vec{q_{10}}\cdot\vec{k_{10}}^T\end{array}\right) =\left(\begin{array}{ccc}s_{1-1} & \cdots & s_{1-10} \\\vdots & \cdots & \vdots \\s_{10-1} & \cdots & s_{10-10}\end{array}\right)
Q?KT∈Rm×m=
?q1???q10???
??(k1??T?k10??T)
?q1???k1??T?q10???k1??T?????q1???k10??T?q10???k10??T?
?=
?s1?1??s10?1??????s1?10??s10?10??
?
矩阵 S S S中的每一个元素通过分别来自于 Q \mathbf{Q} Q 和 K \mathbf{K} K的两个向量的点乘得到的,通过最原始的矩阵定义,可以得知两个向量的点乘意味着一个向量在另一个向量的投影,也可以李继伟表示向量 q i ? \vec{q_{i}} qi??, k j ? \vec{k_j} kj??的相似程度
第二步:scaling与归一化
除以一个数字 d k \sqrt{d_{k}} dk??的意义是:
- 因为如果 d k d_k dk?太大,点乘的值太大,如果不做scaling,结果就没有加法注意力好。
- 为了不让输入太大,导致
softmax函数被推动到非常平缓的区域。
将得到scaling后的相似度进行Softmax操作,假定Scaling之后相似度矩阵为
(
s
1
?
1
′
?
s
1
?
m
′
?
?
?
s
m
?
1
′
?
s
m
?
m
′
)
=
(
s
1
?
1
/
d
k
?
s
1
?
m
/
d
k
?
?
?
s
m
?
1
/
d
k
?
s
m
?
m
/
d
k
)
\left(\begin{array}{ccc}s'_{1-1} & \cdots & s'_{1-m} \\\vdots & \cdots & \vdots \\ s'_{m-1} & \cdots & s'_{m-m}\end{array}\right) = \left(\begin{array}{ccc}s_{1-1}/\sqrt{d_{k}} & \cdots & s_{1-m}/\sqrt{d_{k}} \\\vdots & \cdots & \vdots \\s_{m-1}/\sqrt{d_{k}} & \cdots & s_{m-m}/\sqrt{d_{k}}\end{array}\right)
?s1?1′??sm?1′??????s1?m′??sm?m′??
?=
?s1?1?/dk???sm?1?/dk???????s1?m?/dk???sm?m?/dk???
?
进行归一化
(
s
1
?
1
′
′
?
s
1
?
m
′
′
?
?
?
s
m
?
1
′
′
?
s
m
?
m
′
)
=
(
e
s
1
?
1
′
∑
i
=
1
m
e
s
1
?
i
′
?
e
s
1
?
m
′
∑
i
=
1
m
e
s
1
?
i
′
?
?
?
e
s
m
?
1
′
∑
i
=
1
m
e
s
m
?
i
′
?
e
s
m
?
m
′
∑
i
=
1
m
e
s
m
?
i
′
)
\left(\begin{array}{ccc}s''_{1-1} & \cdots & s''_{1-m} \\\vdots & \cdots & \vdots \\ s''_{m-1} & \cdots & s'_{m-m}\end{array}\right) = \left(\begin{array}{ccc}\frac{e^{s'_{1-1}}} {\sum_{i=1}^{m} e^{s'_{1-i}} } & \cdots & \frac{e^{s'_{1-m}}} {\sum_{i=1}^{m} e^{s'_{1-i}} } \\\vdots & \cdots & \vdots \\ \frac{e^{s'_{m-1}}} {\sum_{i=1}^{m} e^{s'_{m-i}} } & \cdots & \frac{e^{s'_{m-m}}} {\sum_{i=1}^{m} e^{s'_{m-i}} } \end{array}\right)
?s1?1′′??sm?1′′??????s1?m′′??sm?m′??
?=
?∑i=1m?es1?i′?es1?1′???∑i=1m?esm?i′?esm?1′???????∑i=1m?es1?i′?es1?m′???∑i=1m?esm?i′?esm?m′???
?
如此实现一横行的加权和为1,不同的 v i v_i vi? 向量获得的加权综合为1
第三步:加权输出
针对计算出来的权重
α
i
\alpha_{i}
αi?,通过权重对
V
V
V中所有的values进行加权求和计算,得到Attention向量
(
s
1
?
1
′
?
s
1
?
m
′
?
?
?
s
m
?
1
′
?
s
m
?
m
′
)
(
v
1
?
?
v
m
?
)
\left(\begin{array}{ccc}s'_{1-1} & \cdots & s'_{1-m} \\\vdots & \cdots & \vdots \\ s'_{m-1} & \cdots & s'_{m-m}\end{array}\right)\left(\begin{array}{c}\vec{v_{1}}\\\vdots\\ \vec{v_{m}} \end{array}\right)
?s1?1′??sm?1′??????s1?m′??sm?m′??
?
?v1???vm???
?
3.3 读写IO伪代码
#########Standard Attention Implementation
Require: Matrices Q, K, V ∈ R^{N×d} in HBM.
1: Load Q, K by blocks from HBM, compute S = QK^{T}, write S to HBM.
2: Read S from HBM, compute P = softmax(S), write P to HBM.
3: Load P and V by blocks from HBM, compute O = PV, write O to HBM.
4: Return O.
3.3 关于Attention的总结
- 采用点乘注意力,这种注意力机制对于加法注意力而言,更快,同时更节省空间。
- 把
attention抽象为对value的每个表示(token)进行加权,而加权的weight就是attention weight,而attention weight就是根据query和key计算得到,其意义为:为了用value求出query的结果, 根据query和key来决定注意力应该放在value的哪部分。
4 Flash Attention
4.1 背景分析
在标准注意力实现中,注意力的性能主要受限于内存带宽,是内存受限的。频繁地从HBM中读写 R N × N \mathbb{R}^{N \times N} RN×N的矩阵是影响性能的主要瓶颈。稀疏近似和低秩近似等近似注意力方法虽然减少了计算量FLOPs,但对于内存受限的操作,运行时间的瓶颈是从HBM中读写数据的耗时,减少计算量并不能有效地减少运行时间(wall-clock time)。针对内存受限的标准注意力,Flash Attention是IO感知的,目标是避免频繁地从HBM中读写数据。
4.2 解决方案
从GPU显存分级来看,SRAM的读写速度比HBM高一个数量级,但内存大小要小很多。通过kernel融合的方式,将多个操作融合为一个操作,利用高速的SRAM进行计算,可以减少读写HBM的次数,从而有效减少内存受限操作的运行时间。但SRAM的内存大小有限,不可能一次性计算完整的注意力,因此必须进行分块计算,使得分块计算需要的内存不超过SRAM的大小。
问题一:为什么要进行分块计算呢?
内存受限 --> 减少HBM读写次数 --> kernel融合 --> 满足SRAM的内存大小 --> 分块计算
因此分块大小block_size不能太大,否则会导致存储内容踢出。
问题二:分块计算的难点是什么呢?
注意力机制的计算过程是“矩阵乘法 --> scale --> mask --> softmax --> dropout --> 矩阵乘法”,矩阵乘法和逐点操作(scale,mask,dropout)的分块计算是容易实现的,难点在于softmax的分块计算。由于计算softmax的归一化因子(分母)时,需要获取到完整的输入数据,进行分块计算的难度比较大。论文中也是重点对softmax的分块计算进行了阐述。
tiling的主要思想是分块计算注意力。分块计算的难点在于softmax的分块计算,softmax与矩阵 K K K 的列是耦合的,通过引入了两个额外的统计量 m ( x ) m(x) m(x), l ( x ) l(x) l(x)来进行解耦,实现了分块计算。需要注意的是,可以利用GPU多线程同时并行计算多个block的softmax。为了充分利用硬件性能,多个block的计算不是串行(sequential)的, 而是并行的。
4.3 前向算法伪代码:Softmax的IO缩减
一个简单的例子实现分块计算Softmax
对向量 A = [ 1 , 2 , 3 , 4 ] A = [1,2,3,4] A=[1,2,3,4] 计算Softmax,分成两块 A 1 = [ 1 , 2 ] A_1 = [1,2] A1?=[1,2] 和 A 2 = [ 3 , 4 ] A_2 = [3,4] A2?=[3,4] 进行计算。 计算block1和block2:
block1
m
1
=
m
a
x
(
[
1
,
2
]
)
=
2
f
1
=
[
e
1
?
m
1
,
e
2
?
m
1
]
=
[
e
?
1
,
e
0
]
l
1
=
∑
f
1
=
e
?
1
+
e
0
o
1
=
f
1
l
1
=
[
e
?
1
,
e
0
]
e
?
1
+
e
0
=
[
e
?
1
e
?
1
+
e
0
,
e
0
e
?
1
+
e
0
]
m_1 = max([1,2]) = 2\\ f_1 = [e^{1-m_1},e^{2-m_1}] = [e^{-1},e^0]\\ l_1 = \sum f_1 = e^{-1} + e^0\\ o_1 = \frac{f_1}{l_1} = \frac{[e^{-1},e^0]}{e^{-1} + e^0} = \left[ \frac{e^{-1}}{e^{-1} + e^0}, \frac{e^0}{e^{-1} + e^0}\right]
m1?=max([1,2])=2f1?=[e1?m1?,e2?m1?]=[e?1,e0]l1?=∑f1?=e?1+e0o1?=l1?f1??=e?1+e0[e?1,e0]?=[e?1+e0e?1?,e?1+e0e0?]
block2
m
2
=
m
a
x
(
[
3
,
4
]
)
=
4
f
2
=
[
e
3
?
m
2
,
e
4
?
m
2
]
=
[
e
?
1
,
e
0
]
l
2
=
∑
f
2
=
e
?
1
+
e
0
o
2
=
f
2
l
2
=
[
e
?
1
,
e
0
]
e
?
1
+
e
0
=
[
e
?
1
e
?
1
+
e
0
,
e
0
e
?
1
+
e
0
]
m_2 = max([3,4]) = 4\\ f_2 = [e^{3-m_2},e^{4-m_2}] = [e^{-1},e^0]\\ l_2 = \sum f_2 = e^{-1} + e^0\\ o_2 = \frac{f_2}{l_2} = \frac{[e^{-1},e^0]}{e^{-1} + e^0} = \left[ \frac{e^{-1}}{e^{-1} + e^0}, \frac{e^0}{e^{-1} + e^0}\right]
m2?=max([3,4])=4f2?=[e3?m2?,e4?m2?]=[e?1,e0]l2?=∑f2?=e?1+e0o2?=l2?f2??=e?1+e0[e?1,e0]?=[e?1+e0e?1?,e?1+e0e0?]
合并得到完整的softmax结果:
m
=
m
a
x
(
m
a
x
1
,
m
a
x
2
)
=
4
f
=
[
e
m
1
?
m
f
1
,
e
m
2
?
m
?
f
2
]
=
[
e
?
3
,
e
?
2
,
e
?
1
,
e
0
]
l
=
e
m
1
?
m
l
1
,
e
m
2
?
m
?
l
2
=
e
?
3
+
e
?
2
+
e
?
1
+
e
0
o
=
f
l
=
[
e
?
1
,
e
0
]
e
?
1
+
e
0
=
[
e
?
1
e
?
1
+
e
0
,
e
0
e
?
1
+
e
0
]
m = max(max_1,max_2) = 4\\ f = \left[e^{m_1-m}f_1,e^{m_2-m}*f_2\right] = \left[e^{-3},e^{-2},e^{-1},e^0\right]\\ l = e^{m_1-m}l_1,e^{m_2-m}*l_2 = e^{-3}+e^{-2}+e^{-1}+e^0\\ o = \frac{f}{l} = \frac{[e^{-1},e^0]}{e^{-1} + e^0} = \left[ \frac{e^{-1}}{e^{-1} + e^0}, \frac{e^0}{e^{-1} + e^0}\right]
m=max(max1?,max2?)=4f=[em1??mf1?,em2??m?f2?]=[e?3,e?2,e?1,e0]l=em1??ml1?,em2??m?l2?=e?3+e?2+e?1+e0o=lf?=e?1+e0[e?1,e0]?=[e?1+e0e?1?,e?1+e0e0?]
算法伪代码

备注:这是在在忽略mask和dropout的情况下,简化分析Flash Attention算法的前向计算过程
作用分析:
在Flash Attention的前向计算算法中可以看出,FlashAttention实现在不访问整个输入的情况下计算softmax,实现IO的较大缩减,标准Attention算法由于要计算softmax,而softmax都是按行来计算的,即在和 V \mathbf{V} V做矩阵乘之前,需要让 Q \mathbf{Q} Q、 K \mathbf{K} K 的各个分块完成整一行分块的计算得到Softmax的结果后,再和矩阵 V \mathbf{V} V分块做矩阵乘。而在Flash Attention中,将输入分割成块,并在输入块上进行多次传递,从而以增量方式执行softmax缩减。
4.4 后向回传伪代码
将前文的前向计算抽象成如下模型,便于后文的引用
S
=
τ
Q
K
?
∈
R
N
×
N
S
masked?
=
M
A
S
K
(
S
)
∈
R
N
×
N
P
=
softmax
?
(
S
masked?
)
∈
R
N
×
N
P
dropped?
=
dropout
?
(
P
,
p
drop?
)
∈
R
N
×
N
O
=
P
dropped?
V
∈
R
N
×
d
\begin{gathered} S=\tau Q K^{\top} \in \mathbb{R}^{N \times N} \\ S^{\text {masked }}=M A S K(S) \in \mathbb{R}^{N \times N} \\ P=\operatorname{softmax}\left(S^{\text {masked }}\right) \in \mathbb{R}^{N \times N} \\ P^{\text {dropped }}=\operatorname{dropout}\left(P, p_{\text {drop }}\right) \in \mathbb{R}^{N \times N} \\ O=P^{\text {dropped }} V \in \mathbb{R}^{N \times d} \end{gathered}
S=τQK?∈RN×NSmasked?=MASK(S)∈RN×NP=softmax(Smasked?)∈RN×NPdropped?=dropout(P,pdrop??)∈RN×NO=Pdropped?V∈RN×d?
在标准注意力实现中,后向传递计算
Q
\mathbf{Q}
Q,
K
\mathbf{K}
K,
V
\mathbf{V}
V的梯度时,需要用到中间矩阵
S
∈
R
N
×
N
\mathbf{S}\in\mathbb{R}^{N\times N}
S∈RN×N,
P
∈
R
N
×
N
\mathbf{P}\in\mathbb{R}^{N\times N}
P∈RN×N。Flash Attention没有保存这两个矩阵,而是保存了两个统计量
m
(
x
)
m(x)
m(x),
l
(
x
)
l(x)
l(x),在后向传递时进行重计算。
在反向传递过程中, 需要计算损失函数 ? \phi ? 对 O \mathbf{O} O, Q \mathbf{Q} Q, K \mathbf{K} K, V \mathbf{V} V 的梯度。在给定 d O ∈ R N × d d \mathbf{O} \in \mathbb{R}^{N \times d} dO∈RN×d 的情况下, 计算梯度 d Q ∈ R N × d d\mathbf{Q}\in \mathbb{R}^{N \times d} dQ∈RN×d, d K ∈ R N × d d\mathbf{K}\in \mathbb{R}^{N \times d} dK∈RN×d, d V ∈ R N × d d\mathbf{V} \in \mathbb{R}^{N \times d} dV∈RN×d 。其中, d O d\mathbf{O} dO, d Q d\mathbf{Q} dQ, d K d\mathbf{K} dK, d V d\mathbf{V} dV 分别表示为 ? ? ? O \frac{\partial \phi}{\partial \mathbf{O}} ?O???, ? ? ? Q \frac{\partial \phi}{\partial \mathbf{Q}} ?Q???, ? ? ? K \frac{\partial \phi}{\partial \mathbf{K}} ?K???, ? ? ? V \frac{\partial \phi}{\partial \mathbf{V}} ?V???
计算 d V d\mathbf{V} dV
梯度
d
V
d\mathbf{V}
dV 是容易计算的。由
O
=
P
V
\mathbf{O}=\mathbf{P} \mathbf{V}
O=PV,基于矩阵求导算法和链式法则, 得到矩阵形式的梯度
d
V
=
P
?
d
O
d\mathbf{V}=\mathbf{P}^{\top} d \mathbf{O}
dV=P?dO 。在元素形式上,有:
d
v
j
=
∑
i
P
i
j
d
o
i
=
∑
i
e
(
q
i
?
k
j
)
L
i
d
o
i
d \mathbf{v}_j=\sum_i \mathbf{P}_{i j} d \mathbf{o}_i=\sum_i \frac{e^{(\mathbf{q}_i^{\top} k_j)}}{L_i} d \mathbf{o}_i
dvj?=i∑?Pij?doi?=i∑?Li?e(qi??kj?)?doi?
之前已经计算好
L
i
L_i
Li?,就可以通过反复累加的方式计算得到
d
v
j
d \mathbf{v}_j
dvj? 。
计算 d Q d\mathbf{Q} dQ, d K d\mathbf{K} dK
梯度
d
Q
d\mathbf{Q}
dQ,
K
\mathbf{K}
K 的计算是略微复杂的。首先要计算
d
P
d\mathbf{P}
dP,
d
S
d\mathbf{S}
dS 。由
O
=
P
V
\mathbf{O}=\mathbf{P} \mathbf{V}
O=PV,得到矩阵形式的梯度
d
P
=
d
O
V
?
d\mathbf{P}=d\mathbf{O} \mathbf{V}^{\top}
dP=dOV? 。在元素形式上,有:
d
P
i
j
=
d
o
i
?
v
j
d \mathbf{P}_{i j}=d \mathbf{o}_i^{\top} \mathbf{v}_j
dPij?=doi??vj?
有
P
i
:
=
softmax
?
(
S
i
:
)
\mathbf{P}_{i:}=\operatorname{softmax}\left(\mathbf{S}_{i:}\right)
Pi:?=softmax(Si:?) (表示
i
i
i的一整行)。基于
y
=
softmax
?
(
x
)
y=\operatorname{softmax}(x)
y=softmax(x) 的雅各比矩阵为
diag
?
(
y
)
?
y
y
?
\operatorname{diag}(y)-y y^{\top}
diag(y)?yy? 。可以得到:
d
S
i
:
=
(
diag
?
(
P
i
:
)
?
P
i
:
P
i
:
?
)
d
P
i
:
=
P
i
:
°
d
P
i
:
?
(
P
i
:
?
d
P
i
:
)
P
i
:
d \mathbf{S}_{i:}=\left(\operatorname{diag}\left(\mathbf{P}_{i:}\right)-\mathbf{P}_{i:} P_{i:}^{\top}\right) d \mathbf{P}_{i:}=\mathbf{P}_{i:} \circ d \mathbf{P}_{i:}-\left(P_{i:}^{\top} d \mathbf{P}_{i:}\right) \mathbf{P}_{i:}
dSi:?=(diag(Pi:?)?Pi:?Pi:??)dPi:?=Pi:?°dPi:??(Pi:??dPi:?)Pi:?
其中 ° \circ ° 表示逐点相乘。
可以定义:
D
i
=
P
i
:
?
d
P
i
:
=
∑
j
e
q
i
?
k
j
L
i
d
o
i
?
v
j
=
d
o
i
?
∑
j
e
q
i
?
k
j
L
i
v
j
=
d
o
i
?
o
i
D_i=P_{i:}^{\top} d P_{i:}=\sum_j \frac{e^{q_i^{\top} k_j}}{L_i} d o_i^{\top} v_j=d o_i^{\top} \sum_j \frac{e^{q_i^{\top} k_j}}{L_i} v_j=d o_i^{\top} o_i
Di?=Pi:??dPi:?=j∑?Li?eqi??kj??doi??vj?=doi??j∑?Li?eqi??kj??vj?=doi??oi?
将该定义代回到上式中, 可以得到:
d
S
i
:
=
P
i
:
°
d
P
i
:
?
D
i
P
i
:
d S_{i:}=P_{i:} \circ d P_{i:}-D_i P_{i:}
dSi:?=Pi:?°dPi:??Di?Pi:?
因此,梯度
d
S
d\mathbf{S}
dS 可以表示为以下形式:
d
S
i
j
=
P
i
j
d
P
i
j
?
D
i
P
i
j
=
P
i
j
(
d
P
i
j
?
D
i
)
d \mathbf{S}_{i j}=\mathbf{P}_{i j} d \mathbf{P}_{i j}-\mathbf{D}_i \mathbf{P}_{i j}=\mathbf{P}_{i j}\left(d \mathbf{P}_{i j}-\mathbf{D}_i\right)
dSij?=Pij?dPij??Di?Pij?=Pij?(dPij??Di?)
在计算得到
d
P
i
j
d \mathbf{P}_{i j}
dPij?,
d
S
i
j
d \mathbf{S}_{i j}
dSij? 后, 可以计算
d
Q
d\mathbf{Q}
dQ,
d
K
d\mathbf{K}
dK 。有前向计算公式
S
i
j
=
q
i
?
k
j
\mathbf{S}_{i j}=\mathbf{q}_i^{\top} \mathbf{k}_j
Sij?=qi??kj?, 可以得到:
d
q
i
=
∑
j
d
S
i
j
k
j
=
∑
j
P
i
j
(
d
P
i
j
?
D
i
)
k
j
=
∑
j
e
(
q
i
?
k
j
)
L
i
(
d
o
i
?
v
j
?
D
i
)
k
j
d
k
j
=
∑
i
d
S
i
j
q
i
=
∑
i
P
i
j
(
d
P
i
j
?
D
i
)
q
i
=
∑
i
e
(
q
i
?
k
j
)
L
i
(
d
o
i
?
v
j
?
D
i
)
q
i
\begin{gathered} d \mathbf{q}_i=\sum_j d \mathbf{S}_{i j} \mathbf{k}_j=\sum_j \mathbf{P}_{i j}\left(d \mathbf{P}_{i j}-\mathbf{D}_i\right) \mathbf{k}_j=\sum_j \frac{e^{(\mathbf{q}_i^{\top} \mathbf{k}_j)}}{\mathbf{L}_i}\left(d \mathbf{o}_i^{\top} \mathbf{v}_j-\mathbf{D}_i\right) \mathbf{k}_j \\ d \mathbf{k}_j=\sum_i d \mathbf{S}_{i j} \mathbf{q}_i=\sum_i \mathbf{P}_{i j}\left(d \mathbf{P}_{i j}-\mathbf{D}_i\right) \mathbf{q}_i=\sum_i \frac{e^{(\mathbf{q}_i^{\top} \mathbf{k}_j)}}{\mathbf{L}_i}\left(d \mathbf{o}_i^{\top} \mathbf{v}_j-\mathbf{D}_i\right) \mathbf{q}_i \end{gathered}
dqi?=j∑?dSij?kj?=j∑?Pij?(dPij??Di?)kj?=j∑?Li?e(qi??kj?)?(doi??vj??Di?)kj?dkj?=i∑?dSij?qi?=i∑?Pij?(dPij??Di?)qi?=i∑?Li?e(qi??kj?)?(doi??vj??Di?)qi??
与前向计算类似,在计算得到 L i \mathbf{L}_i Li? 后, 就可以通过反复累加的方式计算得到 d q i d \mathbf{q}_i dqi?, d k j d \mathbf{k}_j dkj?, d v j d \mathbf{v}_j dvj? 。避免了实例化矩阵 P \mathbf{P} P, S \mathbf{S} S,节省了显存,后向传递的显存复杂度为 O ( N ) O(N) O(N) 。
作用分析
对比标准Attention算法的实现过程中,其需要将计算中的 S \mathbf{S} S、 P \mathbf{P} P写入到HBM中,而这些中间矩阵的大小与输入的序列长度有关且为二次型;
Flash Attention算法中,其并没有将 S \mathbf{S} S、 P \mathbf{P} P写入HBM中去,而是通过分块写入到HBM中去,存储前向传递的 softmax 归一化因子,在后向传播中快速重新计算片上注意力,这比从HBM中读取中间注意力矩阵的标准方法更快。即使由于重新计算导致 FLOPS 增加,但其运行速度更快并且使用更少的内存(序列长度线性),主要是因为大大减少了 HBM 访问量。
Flash Attention实现了不使用中间注意力矩阵,通过存储归一化因子来减少HBM内存的消耗。
5 总结
- FA尽可能避免从HBM中读取和写入注意力矩阵,做到了:
- 在不访问整个输入的情况下计算softmax函数的IO缩减;
- 在后向传播中不存储中间注意力矩阵
- 通过减少GPU内存读取/写入,FlashAttention的运行速度比PyTorch标准注意力快 2-4 倍,所需内存减少5-20倍。
6 参考文献
[2205.14135] FlashAttention: Fast and Memory-Efficient Exact Attention with IO-Awareness
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!