【Python 零基础入门】函数

2023-12-14 14:27:53

【Python 零基础入门】第五课函数

当我们首次接触到编程时, 我们往往会听到 “函数” 这个概念. 那么问题来了, 函数到底是什么? 为什么函数在编程中如此重要? 简而言之, 函数是一个独立的代码块, 可以帮助我们执行某个特定的任务. 你可以将函数想象成一个机器人, 帮我我们来执行任务. 我们给它输入, 处理后, 返回给我们一个输出. 在代码中使用函数不仅能使得代码有更好的可读性, 而且能帮助我们避免重复 & 减少错误.

Python 零基础入门函数

函数在生活中的类比

想象一下, 每天早晨你都会做同样的事情: 起床, 洗脸, 刷牙, 吃早餐. 现在, 如果每天你都要详细列出这些步骤, 那么一段时间后, 这会变得非常枯燥和重复. 相反, 你可能更倾向于简单地说: “我正在做我的早晨例行公事”. 这就是函数在编程中的作用. 它允许你将一个任务的所有步骤封装在一个定义良好的代码块中, 然后通过一个简单的函数调用来执行它.

函数

函数 (Function) 是一段可以帮助我们实现我们想要功能的代码段. 函数可以重复使用, 我们也可以自定义函数. 在 Python 中, 函数可以帮助我们, 执行单一的, 相关的操作. 函数可以提高应用的模块性, 并提高代码的复用率. Python 为我们提供了许多内置函数, 如print(), 但我们也可以自己创建函数, 这些被称为自定义函数.

在这里插入图片描述

为什么要使用函数

函数 (Function) 提供了一种将复杂问题拆分的方法. 通过定义函数, 我们可以避免重复相同的代码, 提高程序可读性, 以便更好的维护.

函数的格式

在 Python 中, 我们可以使用 “def” 关键字来定义函数. 函数可以带参数也可以不带参数.

格式:

# 定义函数
def 函数名(参数1, 参数2, 参数3...):
	函数主体

定义了函数之后, 我们可以通过函数名来调用函数, 并传递必要的参数:

# 调用函数
函数名(参数1, 参数2, 参数3...)

无参函数

例子:

# 定义无参函数
def func():
    print("祖国你好")

# 调用函数
func()

输出结果:

祖国你好

含参函数

例子:

# 定义函数
def num_compare(num1, num2):
    # 条件判断, 比较数字大小
    if num1 > num2:
        print("第一个数字大")
    elif num1 == num2:
        print("两个数字相同")
    else:
        print("第二个数字大")

# 调用函数
num_compare(1, 2)

输出结果:

第二个数字大

更优的写法:

# 定义函数
def num_compare(num1, num2):
    # 判断传入的参数是否为数字
    if str(num1).isdigit() == False or str(num2).isdigit() == False:
        print("参数必须为数字")
        return  # 跳出函数

    # 条件判断, 比较数字大小
    if num1 > num2:
        print("第一个数字大")
    elif num1 == num2:
        print("两个数字相同")
    else:
        print("第二个数字大")

# 调用函数
num_compare("a", 2)
num_compare("c", "d")
num_compare(1, 2)

输出结果:

参数必须为数字
参数必须为数字
第二个数字大

我们将传入的参数转换为字符串 (String), 然后通过函数isdigit()判断是否为数字, 避免了可能会发生的错误.

参数

参数 (Parameter)

Python 中的参数有两大类:

形式参数
实际参数

在这里插入图片描述

形参

形参 (形式参数), 是在函数定义, 的时候命名的参数.

例子:

# 定义函数
def sum(num1, num2):  # num1, num2为形式参数
    # 返回求和
    return num1 + num2
    
# 获取结果
total = sum(2, 3)  # 2, 3为实际参数
print(total)

输出结果:

实参

实参 (实际参数) 是在实际执行是, 传递给函数的参数. 形参相当于实参的一个副本.

例子:

# 定义函数
def multi(num1, num2):  # num1, num2为形式参数

    # 返回乘积
    return num1 *num2


# 获取结果
total = multi(2, 3)  # 2, 3为实际参数
print(total)

输出结果:

变量

作用域

作用域 (Scope) 是函数中的一个重要概念. 函数内部什么的变量是局部变量 (Local Variable) 仅在函数内有效, 而在函数外部声明的变量属于全局变量 (Global Variable), 作用域为全局.

局部变量

局部变量 (Local Variable) 只能在变量所在的函数内使用. 当我们创建局部变量时, 内存中会临时分配一块空间, 当函数执行完该临时空间就会被回收.

例子:

# 定义函数
def func():
    # 局部变量
    a = 10
    b = 20

    # 调试输出
    print("函数内")
    print(a)
    print(b)

# 调用函数
func()

# 在函数外调用变量 (报错)
print("函数外")
print(a)
print(b)

输出结果:

Traceback (most recent call last):
  File "C:/Users/Windows/Desktop/讲课/第五课 函数/第五课 局部变量.py", line 17, in <module>
    print(a)
NameError: name 'a' is not defined
函数内
10
20
函数外

注意: 局部变量无法在函数外调用

全局变量

例子:

# 在函数体外定义的变量为全局变量
a = 10

# 定义函数
def func():
    # 使用global修饰符在函数内申明变量
    global b
    b = 10

    # 调试输出
    print("函数内")
    print(a)
    print(b)


# 调用函数
func()

# 输出结果
print("函数外")
print(a)
print(b)

输出结果:

函数内
10
10
函数外
10
10

递归函数

递归函数 (Recursive Functions) 是一种自己调用自己的函数. 使用递归函数可以解决很多问题, 例如计算接触货斐波那契数列.

格式:

def 递归函数(参数):
    if 停止条件:  # 也被称为基线条件 (base case)
        return 基线结果
    else:
        # 更新参数，通常是减小问题规模
        新参数 = 更新参数(参数) 
        return 一些操作 + 递归函数(新参数)

基本的递归

阶乘的例子:

5! = 5 × 4 × 3 × 2 × 1 = 120

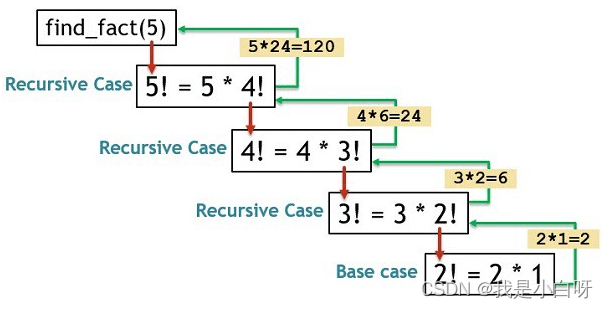
在这里插入图片描述

定义一个递归函数来计算阶乘:

# 定义阶乘函数
def factorial(n):
    if n == 1:
        return 1
    else:
        # 递归
        return n * factorial(n - 1)

print(factorial(5))

输出结果:

斐波那契数列

讲一下递归中讲点的例子, 斐波那契数列 (Fibonacci Sequence) 的前两个数字是 0 和 1, 之后每个数字都是前两个数字的和:

# 定义斐波那契函数
def fibonacci(n):

    # 停止条件
    if n <= 1:
        return n

    # 递归, 前两数相加
    return fibonacci(n-1) + fibonacci(n-2)

print(fibonacci(7))

输出结果:

120
13

Lambda 表达式

Lambda 表达式又被称为匿名函数, 因为 Lambda 表达式没有具体的名字.

例子:

# 基本的算术操作
f = lambda x, y: x + y  # 加法
print(f(2, 3))  # 输出: 5

# 字符串操作
capitalize = lambda s: s.capitalize()  # 大写
print(capitalize('hello'))  # 输出: Hello

# 逻辑操作
is_even = lambda x: x % 2 == 0
print(is_even(4))  # 输出: True

# 列表操作
get_last = lambda x: x[-1]  # 取最后元素
print(get_last([1, 2, 3, 4]))  # 输出: 4

# 条件操作
check_sign = lambda x: 'positive' if x > 0 else 'negative' if x < 0 else 'zero'
print(check_sign(-5))  # 输出: negative

# 函数作为参数
numbers = [1, 2, 3, 4]
squared = map(lambda x: x**2, numbers)
print(list(squared))  # 输出: [1, 4, 9, 16]

高阶函数

下面我们来讲一下 Python 中常用的高阶函数. Python 中的内置函数map(), filter(), reduce()都是高阶函数的例子.

map 函数

map()函数可以将一个函数应用于一个或多个可迭代对象.

格式:

map(function, iterables)

参数:

function: 函数
iterables: 可迭代函数, 比如数组

例子:

# 创建数组
numbers = [1, 2, 3, 4]
squared = map(lambda x: x**2, numbers)  
print(list(squared))

输出结果:

[1, 4, 9, 16]

filter 函数

filter()函数用于过滤可迭代对象, 返回一个迭代器.

# 创建数组
numbers = [1, 2, 3, 4, 5]
even_numbers = filter(lambda x: x % 2 == 0, numbers)  # 使用 Lambda 进行筛选
print(list(even_numbers))

输出结果:

[2, 4]

reduce 函数

reduce()函数连续地应用函数到一个序列上, 从左到右, 以减少该序列一个个的值. 我们可以使用reduce()来对所有元素进行求和.

例子:

from functools import reduce


# 创建数组
numbers = [1, 2, 3, 4]
result = reduce(lambda x, y: x + y, numbers)
print(result)

输出结果:

结合

先使用map()计算每个数字的平方, 然后使用filter()函数过滤出偶数平方.

# 创建数组
numbers = [1, 2, 3, 4, 5]
squared = map(lambda x: x**2, numbers)
even_squares = filter(lambda x: x % 2 == 0, squared)
print(list(even_squares))

输出结果:

[4, 16]

高阶函数的好处:

使用高阶函数可以使得我们的代码更简洁, 易读. 高阶函数允许我们在更高的层次上考虑的的代码逻辑, 而不是深陷于循环和条件语句的细节.

Python 装饰器 (了解)

装饰器 (Decorator) 是 Python 的一个强大工具, 允许我们在不修改原有代码的情况下增加函数或方法.

基础装饰器

下面是一个基础装饰器, 会在函数运行前后都输出一条信息:

# 定义装饰器
def simple_decorator(func):
    """
    基础装饰器
    :param func: 函数作为参数
    :return: 包装函数
    """
    def wrapper():
        print("函数运行前")
        func()
        print("函数运行后")
    return wrapper

# 使用装饰器
@simple_decorator
def hello():
    print("Hello, World!")

# 调用函数
hello()

输出结果:

函数运行前
Hello, World!
函数运行后

参数化装饰器

def repeat(num):
    def decorator(func):
        def wrapper(*args, **kwargs):
            for _ in range(num):
                func(*args, **kwargs)
        return wrapper
    return decorator

@repeat(num=3)
def greet(name):
    print(f"Hello, {name}!")

greet("我是小白呀")

输出结果:

Hello, 我是小白呀!
Hello, 我是小白呀!
Hello, 我是小白呀!

生成器 (了解)

生成器 (Generator) 是 Python 中的一种迭代器, 允许我们在迭代时动态生成值, 而不是预先在内存中存储它们.

基础生成器

通过使用yield关键字, 创建一个简单的生成器.

例子:

def simple_generator():
    yield 1
    yield 2
    yield 3

gen = simple_generator()
print(next(gen))  # 输出: 1
print(next(gen))  # 输出: 2

输出结果:

1
2

生成器表达式

例子:

squared = (x*x for x in range(5))
print(next(squared))  # 输出: 0
print(next(squared))  # 输出: 1

输出结果:

0
1

总结

函数是编程中的核心构建块之一, 它们不仅提供了一种组织和复用代码的方式, 还为代码的模块化提供了一种手段。通过这篇博客, 我们已经探讨了 Python 中函数的各个方面, 从基础的函数定义和调用, 到参数传递, 再到更高级的概念, 如闭包, 装饰器和高阶函数.

我们学习了如何使用默认参数, 关键字参数和可变参数来给函数提供更大的灵活性. 同时, 我们也了解了如何使用返回值来将数据从函数传回给调用者.

在深入研究高阶函数时, 我们发现 Python 的函数是一等公民, 可以像其他对象一样被传递和返回. 这为我们提供了强大的工具, 如 map()、filter() 和 reduce(), 使我们能够编写更简洁和高效的代码.

练习

基础函数练习

练习 1:

编写一个函数，接受两个数字参数并返回它们的和
练习 2:
编写一个函数，接受一个字符串参数并返回其反转字符串
练习 3:
创建一个函数，接受一个整数列表并返回其平均值

递归练习

练习:

设计一个递归函数，检查一个字符串是否是回文

Lambda 表达式

练习 1:

使用 filter() 函数和 lambda 表达式从一个整数列表中筛选出平方数
练习 2:
使用 map() 函数和 lambda 表达式将一个整数列表中的每个数字立方
练习 3:
使用 reduce() 函数和 lambda 表达式计算数字列表的乘积
练习 4:
在不使用切片的情况下, 使用 lambda 表达式反转列表

答案

基础函数练习

练习 1:

"""
@Module Name: 基础函数练习.py
@Author: CSDN@我是小白呀
@Date: October 11, 2023

Description:
基础函数练习
"""


# 定义函数
def add(num1, num2):
    return num1 + num2

# 调用函数
print("两数之和:", add(1, 2))

输出结果:

两数之和: 3

练习 2:

"""
@Module Name: 基础函数练习.py
@Author: CSDN@我是小白呀
@Date: October 11, 2023

Description:
基础函数练习
"""


# 定义函数
def reverse_string(str):
    str_list = list(str)
    result = "".join(str_list[::-1])
    return result

# 调用函数
print("反转字符串:", reverse_string("我是小白呀"))

输出结果:

反转字符串: 呀白小是我

练习 3:

"""
@Module Name: 基础函数练习.py
@Author: CSDN@我是小白呀
@Date: October 11, 2023

Description:
基础函数练习
"""


# 定义函数
def average(array):
    return sum(array) / len(array)

# 调用函数
print("数组平均值:", average([1, 2, 3, 4, 5]))

输出结果:

3.0

递归函数

# 定义函数
def func(str):

    # 停止条件
    if len(str) <=1:
        return True

    if str[0] == str[-1]:
        return func(str[1:-1])

    return False

输出结果:

True
False

Lambda 表达式

练习 1:

"""
@Module Name:  Lambda表达式.py
@Author: CSDN@我是小白呀
@Date: October 11, 2023

Description:
Lambda表达式
"""


# 定义列表
array = [1, 2, 3, 4, 5, 6, 7, 8, 9]
print("原始数组:", array)

# Lambda表达式
array_even = list(filter(lambda x:x**0.5 % 1 == 0, array))
print("筛选平方数:", array_even)

输出结果:

原始数组: [1, 2, 3, 4, 5, 6, 7, 8, 9]
筛选平方数: [1, 4, 9]

练习 2:

"""
@Module Name:  Lambda表达式.py
@Author: CSDN@我是小白呀
@Date: October 11, 2023

Description:
Lambda表达式
"""


# 定义列表
array = [1, 2, 3, 4, 5, 6, 7, 8, 9]
print("原始数组:", array)

# Lambda表达式
array_cube = list(map(lambda x:x**3, array))
print("数组立方:", array_cube)

输出结果:

原始数组: [1, 2, 3, 4, 5, 6, 7, 8, 9]
数组立方: [1, 8, 27, 64, 125, 216, 343, 512, 729]

练习 3:

"""
@Module Name:  Lambda表达式.py
@Author: CSDN@我是小白呀
@Date: October 11, 2023

Description:
Lambda表达式
"""


from functools import reduce


# 定义列表
array = [1, 2, 3, 4, 5, 6, 7, 8, 9]
print("原始数组:", array)

# Lambda表达式
result = reduce(lambda x, y:x*y, array)
print("数组乘积:", result)

输出结果:

原始数组: [1, 2, 3, 4, 5, 6, 7, 8, 9]
数组立方: 362880

练习 4:

"""
@Module Name:  Lambda表达式.py
@Author: CSDN@我是小白呀
@Date: October 11, 2023

Description:
Lambda表达式
"""


from functools import reduce


# 定义列表
array = [1, 2, 3, 4, 5, 6, 7, 8, 9]
print("原始数组:", array)

# Lambda表达式
result = reduce(lambda x, y:[y] + x, array, [])
print("反转后的数组:", result)

输出结果:

原始数组: [1, 2, 3, 4, 5, 6, 7, 8, 9]
反转后的数组: [9, 8, 7, 6, 5, 4, 3, 2, 1]

文章来源:https://blog.csdn.net/weixin_46274168/article/details/133765626
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：veading@qq.com进行投诉反馈，一经查实，立即删除！

【Python 零基础入门】 函数

【Python 零基础入门】第五课 函数

【Python 零基础入门】第五课 函数

函数在生活中的类比

函数

为什么要使用函数

函数的格式

无参函数

含参函数

参数

形参

实参

变量

作用域

局部变量

全局变量

递归函数

基本的递归

斐波那契数列

Lambda 表达式

高阶函数

map 函数

filter 函数

reduce 函数

结合

Python 装饰器 (了解)

基础装饰器

参数化装饰器

生成器 (了解)

基础生成器

生成器表达式

总结

练习

基础函数练习

递归练习

Lambda 表达式

答案

基础函数练习

递归函数

Lambda 表达式

【Python 零基础入门】函数

【Python 零基础入门】第五课函数

【Python 零基础入门】第五课函数