Leetcode 40 组合总和 II

题意理解：

1. ????????每个数字在每个组合中只能使用?一次?
2. ????????数字可以重复——>难点（如何去重）
3. ????????每个组合和=target

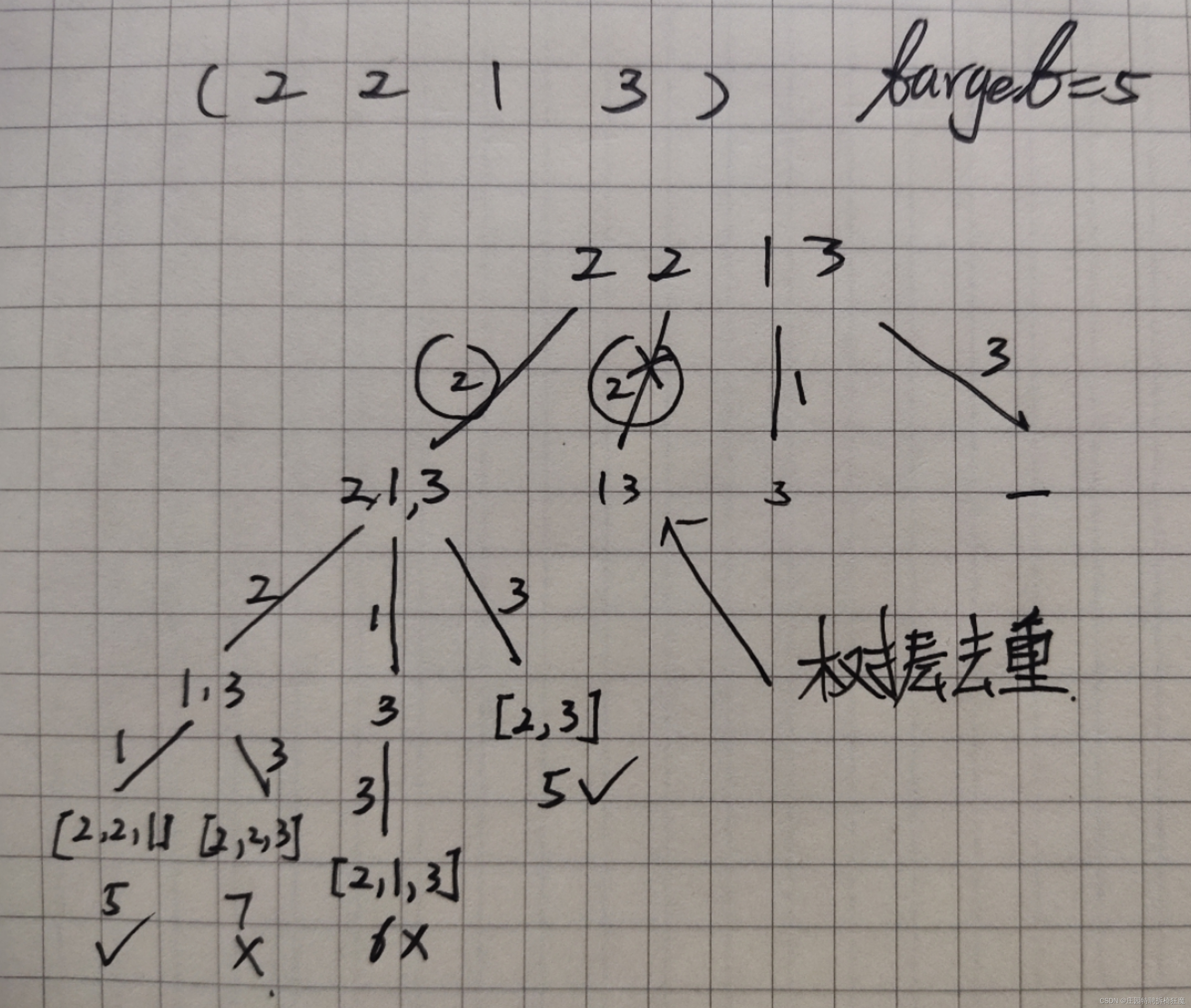
? ? ? ? 求组合，对合限制，考虑回溯的方法。——将其抽象为树结构。

? ? ? ? 树的宽度——分支大小

? ? ? ? 树的深度——最长的组合（和=target）

??去重难点：

????????根据《代码随想录》关于树层去重的引入：

? ? ? ? 第一个位置选2，再次选2的话，下面的分支回出现重复的[2,3]组合。

? ? ? ? 实际上保留第一个分支，之后同一位置相同的数值选项可以剪除。

? ? ? ? 用used[]数组来维护是否被访问的状态。

????????

回溯的方法：

? ? ? ? 1.确定返回值+参数列表

? ? ? ? 2.确定终止条件|剪枝条件

? ? ? ? 3.单层逻辑|回溯操作

1.暴力回溯+剪枝优化

考虑返回值一般为void, 参数包含数组，和目标值，当前数值指示下标

终止条件： sum>=4,特别的sum==4时收集结果。

单层递归逻辑：一定要对sum和path、used数组做好回溯操作。

数层剪枝：candidates[i-1]==candidates[i]遇到重复值

? ? ? ? used[i-1]=true:表示上一个重复的值，在该组合内被用到。

? ? ? ? used[i - 1] == false：表示上一个重复值在该组合内没有用到，应该是同一树层用到——即数层重复，剪枝。

List<List<Integer>> result=new ArrayList<>();
    LinkedList<Integer> path=new LinkedList<>();
    int sum=0;
    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        boolean[] used=new boolean[candidates.length];
        Arrays.sort(candidates);
        Arrays.fill(used, false);
        backtrackig(candidates,target,0,used);
        return result;
    }
    public void backtrackig(int[] candidates, int target,int startIndex,boolean[] used){

        //终止|剪枝
        if(sum>target) return;
        else if (sum==target) {
            result.add(new ArrayList<>(path));
            return;
        }
        //单层递归逻辑
        for(int i=startIndex;i<candidates.length;i++){
            //数层剪枝
            if(i!=0&&candidates[i-1]==candidates[i]&&used[i-1]==false) continue;
            path.add(candidates[i]);
            sum+=candidates[i];
            used[i]=true;
            backtrackig(candidates,target,i+1,used);
            path.removeLast();
            sum-=candidates[i];
            used[i]=false;
        }
    }

注意两个特殊的地方：

Arrays.sort(candidates);//数组排序

Arrays.fill(used, false);//数组填充，实际上该数组默认也是false.

2.分析

时间复杂度：O()

空间复杂度：O(n)