推荐算法：HNSW【推荐出与用户搜索的类似的/用户感兴趣的商品】

HNSW算法概述

HNSW（Hierarchical Navigable Small Word）算法算是目前推荐领域里面常用的ANN（Approximate Nearest Neighbor）算法了。其目的就是在极大量的候选集当中如何快速地找到一个query最近邻的k个元素。

要找到一个query的k个最近邻元素，一个朴素的思想就是我去计算这个query和所有的总量N 个候选元素的距离，然后选择其中的前k 个最小元素，这个经典算法的算法复杂度是O(Nlog(k))，显然这个算法复杂度实在是太高了，无法适用于实际的使用场景。

而要解决这个问题，可以有多种实现方法，这里所要说的HNSW算法就是目前比较常用的一种搜索算法，它算是其前作NSW算法的一个升级版本，但是两者的本质都是基于一个朴素的思路，就是通过图连接的方式给所有的N 个候选元素事先地定义好一个图连接关系，从而可以将前述的算法复杂度当中的N 的部分给减小掉，从而优化整体的检索效率。

其整体的一个图结果可以用下图进行表达：

解决的问题：做高效率相似性查找。推荐系统中，如何找到与用户query最相近的几个item，然后推荐出去【也就是推荐出与用户搜索的类似的/用户感兴趣的商品】。

解决方法有：Annoy，KD-Tree， LSH， PQ，NSW， HNSW等。

近似最近邻搜索算法（Approximate Nearest Neighbor Search，ANNS）发展：近邻图(Proximity Graph)–> NSW --> Skip List --> HNSW

近似最近邻搜索算法（Approximate Nearest Neighbor Search，ANNS）

1. 近邻图(Proximity Graph)

近邻图(Proximity Graph)： 最朴素的图算法

思路： 构建一张图， 每一个顶点连接着最近的 N 个顶点。 Target （红点）是待查询的向量。在搜索时， 选择任意一个顶点出发。 首先遍历它的友节点， 找到距离与 Target 最近的某一节点， 将其设置为起始节点， 再从它的友节点出发进行遍历， 反复迭代， 不断逼近， 最后找到与 Target 距离最近的节点时搜索结束。

存在的问题：

1. 图中的K点无法被查询到。
2. 如果要查找距离Target （红点）最近的topK个点， 而如果点之间无连线， 将影响查找效率。
3. D点有这么多友节点吗？ 增加了构造复杂度。谁是谁的友节点如何确定？
4. 如果初始点选择地不好（比如很远），将进行多步查找。

2. NSW算法原理

NSW，即没有分层的可导航小世界的结构（Navigable-Small-World-Graph ）。

针对上面的问题，解决办法：

1. 某些点无法被查询到 -> 规定构图时所有节点必须有友节点。
2. 相似点不相邻的问题 -> 规定构图时所有距离相近到一定程度的节点必须互为友节点。
3. 关于某些点有过多友节点?-> 规定限制每个节点的友节点数量。
4. 初始点选择地很远 -> 增加高速公路机制。

2.1 NSW构图算法

图中插入新节点时，通过随机存在的一个节点出发查找到距离新节点最近的m个节点（规定最多m个友节点，m由用户设置），连接新节点到这最近的m个节点。节点的友节点在新的节点插入的过程中会不断地被更新。

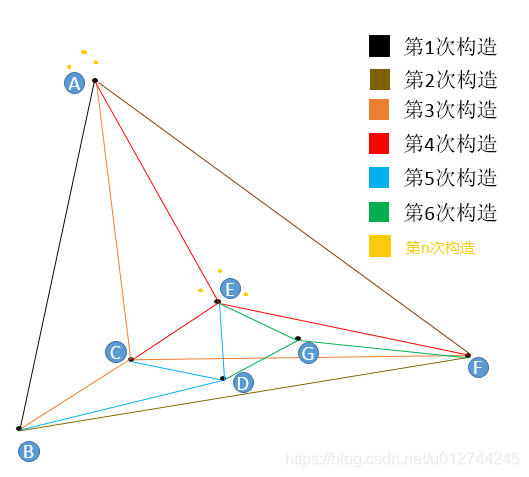
m=3（每个点在插入时找3个紧邻友点）。

第1次构造：图为空，随机插入A，初始点为A。图中只有A，故无法挑选友节点。插入B，B点只有A点可选，所以连接BA。

第2次构造：插入F，F只有A和B可以选，所以连接FA，FB。

第3次构造：插入C，C点只有A，B，F可选，连接CA，CB，CF。

第4次构造：插入E，从A，B，C，F任意一点出发，计算出发点与E的距离和出发点的所有“友节点”和E的距离，选出最近的一点作为新的出发点，如果选出的点就是出发点本身，那么看我们的m等于几，如果不够数，就继续找第二近的点或者第三近的点，本着不找重复点的原则，直到找到3个近点为止。找到了E的三个近点，连接EA，EC，EF。

第5次构造：插入D，与E点的插入一模一样，都是在“现成”的图中查找到3个最近的节点作为“友节点”，并做连接。

第6次构造：插入G，与E点的插入一模一样，都是在“现成”的图中查找到3个最近的节点作为“友节点”，并做连接。

在图构建的早期，很有可能构建出“高速公路”。

第n次构造：在这个图的基础上再插入6个点，这6个点有3个和E很近，有3个和A很近，那么距离E最近的3个点中没有A，距离A最近的3个点中也没有E，但因为A和E是构图早期添加的点，A和E有了连线，我们管这种连线叫“高速公路”，在查找时可以提高查找效率（当进入点为E，待查找距离A很近时，我们可以通过AE连线从E直接到达A，而不是一小步一小步分多次跳转到A）。

结论：一个点，越早插入就越容易形成与之相关的“高速公路”连接，越晚插入就越难形成与之相关的“高速公路”连接。

这个算法设计的妙处就在于扔掉德劳内三角构图法，改用“无脑添加”（NSW朴素插入算法），降低了构图算法时间复杂度的同时还带来了数量有限的“高速公路”，加速了查找。

2.2 NSW查找算法

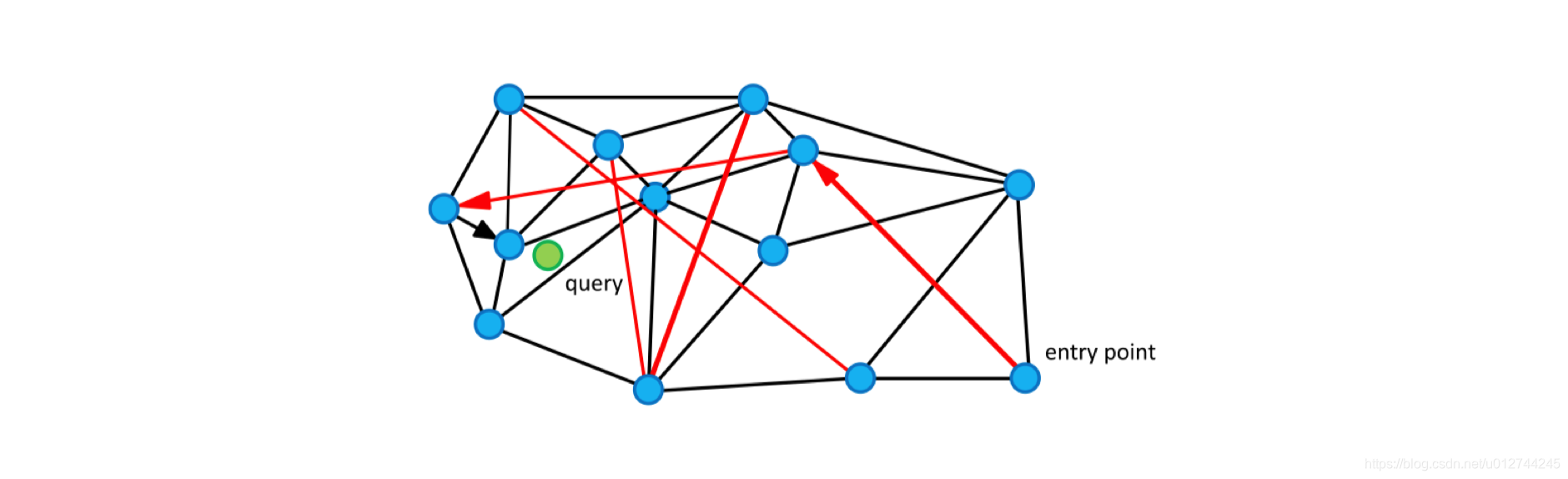
图中的边有两个不同的目的：

1. Short-range edges，用作贪婪搜索算法所需的近似 Delaunay 图。
2. Long-range edges，用于贪婪搜索的对数缩放。负责构造图形的可导航小世界（NSW）属性。

优化查找：

1. 建立一个废弃列表visitedSet，在一次查找任务中遍历过的点不再遍历。
2. 建立一个动态列表result，把距离查找点最近的n个点存储在表中，并行地对这n个点进行同时计算“友节点”和待查找点的距离，在这些“友节点”中选择n个点与动态列表中的n个点进行并集操作，在并集中选出n个最近的友点，更新动态列表。

推荐算法：HNSW算法简介-CSDN博客

检索模型-粗排HNSW_hnsw模型-CSDN博客