【计算机视觉】SIFT

?在边缘提取的时候，用高斯一阶导对信号进行卷积，响应值最大的就是边界如果用高斯二阶导对信号进行卷积，0点就是边界点（二阶导等于0的点，对应一阶导的极值点）

如果用高斯二阶导在不同的信号上进行卷积，当信号宽度与高斯滤波核匹配的时候，就能得到绝对值最大的信号，这样就建立了尺度和滤波核之间的联系。

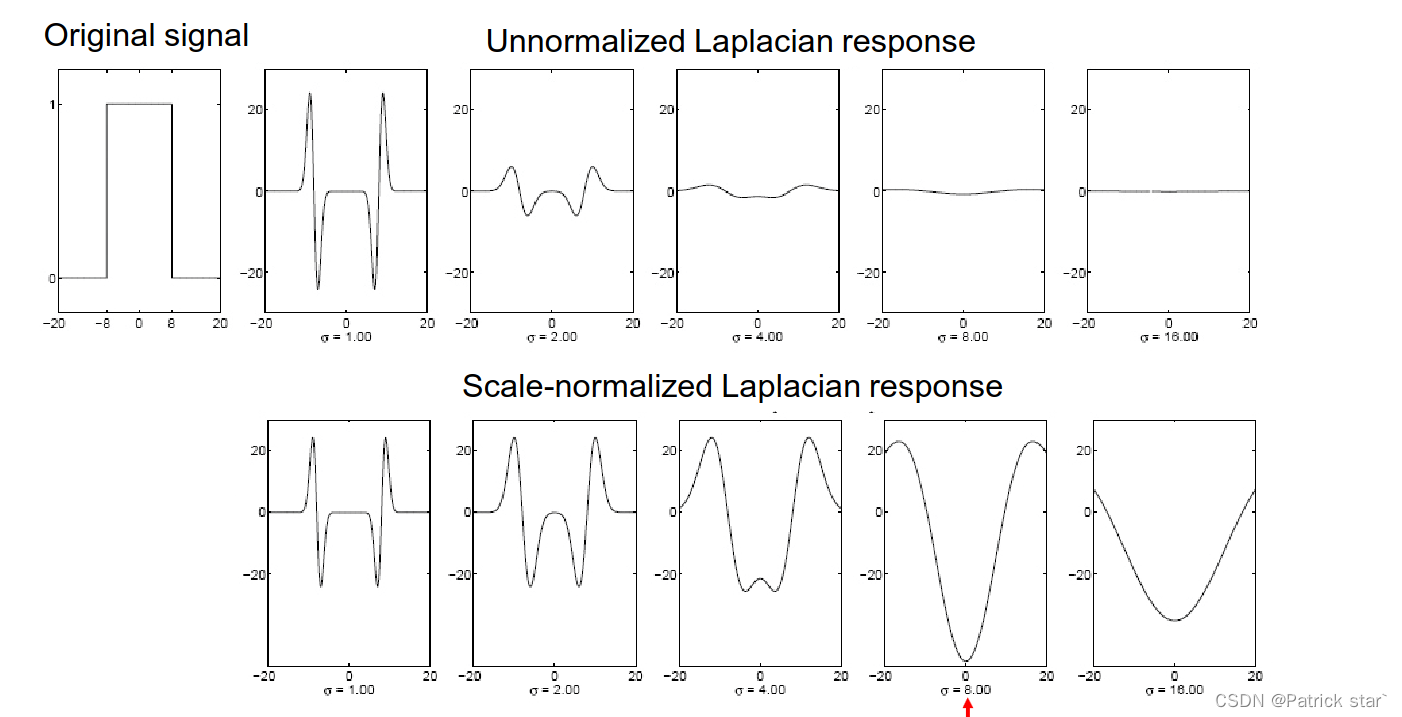
用不同的Laplacian对同一个信号进行卷积的时候，随着的增大，响应值会越来越不明显。

因为作为分母，越来越大，卷积后的信号值就会越来越小 ，对于一阶偏导需要对卷积后的信号补偿，对于二阶偏导需要对卷积后的信息补偿 ，将响应值固定在一个尺度上。

补偿之后，就能用反映尺度

二维Laplacian高斯卷积核如下图所示

当半径值正好与Laplacian为0的值匹配上的时候，响应值最大

假设这个圆是二进制的，简单来说就是让laplacian小于0的部分权值为0，laplacian大于0的部分权值为1

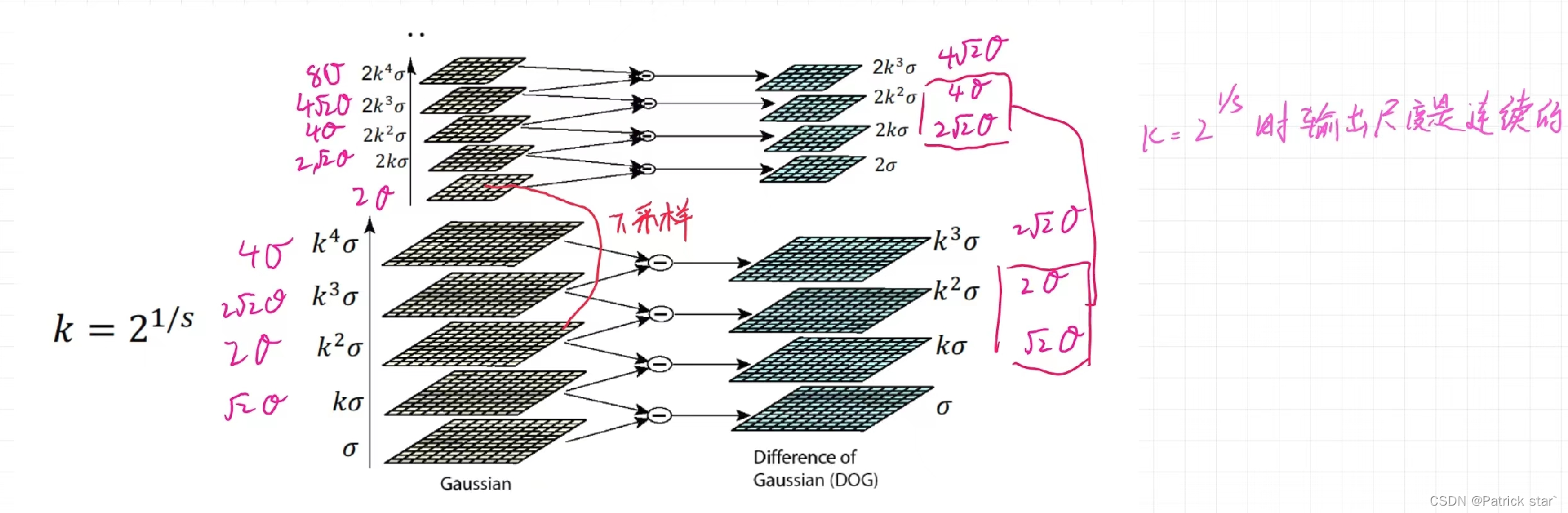
SIFT使用的是DoG模版（两个高斯模版的差分），拥有和Laplacian类似的特性

一般而言，随着的增大，窗口也会变大，Laplacian每一次都会在原图进行卷积，卷积的成本就会增大。而DoG是利用高斯卷积核来做的，可以通过对较小的卷积核卷积得到较大的卷积核，减小卷积成本。

在SIFT算法中，当你需要更大的尺度时候，不是改变，而是按比例缩小原图，用小的进行卷积，然后再将卷积的结果乘以对应比例，只用一套滤波核就能得到多个尺度空间。