【图的应用三:拓扑排序】- 用 C 语言实现拓扑排序
目录
?
一、AOV-网
一个无环的有向图称作有向无环图(Directed Acycline Graph),简称 DAG 图。
有向无环图是描述一项工程或系统的进行过程的有效工具。通常把计划、施工过程、生产流程、程序流程等都当成一个工程。除了很小的工程外,一般的工程都可分为若干个称做活动(Activity)的子工程,而这些子工程之间,通常受着一定条件的约束,如其中某些子工程的开始必须在另一些子工程完成之后。
例如,一个软件专业的学生必须学习一系列课程,其中有些课程是基础课,独立于其他课程,如《高等数学》;而另一些课程必须在学完作为其基础的先修课程才能开始,比如,在《程序设计基础》和《离散数学》学完之前就不能开始学习《数据结构》。这些先决条件定义了课程之间的领先(优先)关系。这个关系可以用有向图更清楚地表示,图中顶点表示课程,有向弧表示先决条件,若课程 i 是课程 j 的先决条件,则图中有弧 <i, j>。
这种用顶点表示活动,用弧表示活动间的优先关系的有向图称为顶点表示活动的网(Activity On Vertex Network),简称 AOV-网。
注意:在 AOV-网中,不应该出现环,即 AOV-网应该是 DAG 图,因为存在环意味着某些活动应以自己为先决条件,显然这是荒谬的。因此,对于给定的 AOV-网应首先判定网中是否存在环,检测的办法是对有向图的顶点进行拓扑排序,若网中的顶点都在它的拓扑有序序列中,则该 AOV-网中必定不存在环。
所谓拓扑排序就是将 AOV-网中所有顶点排成一个线性序列,该序列满足:若在 AOV-网中由顶点 vi 到顶点 vj 有一条路径,则在该线性序列中的顶点 vi 必定在顶点 vj 之前。学生必须按照拓扑有序的顺序来安排学习,这样才能保证学习任一门课程时其先修课程已经学过。
二、拓扑排序的过程
-
在有向图中选择一个无前驱的顶点且输出它。
-
在图中删除该顶点和所有以它为尾的弧。
重复上述两步,直至不存在无前驱的顶点。若此时输出的顶点数小于有向图的顶点数,则说明有向图中存在环,否则输出的顶点序列即为一个拓扑序列。
注意:拓扑序列可能不唯一。
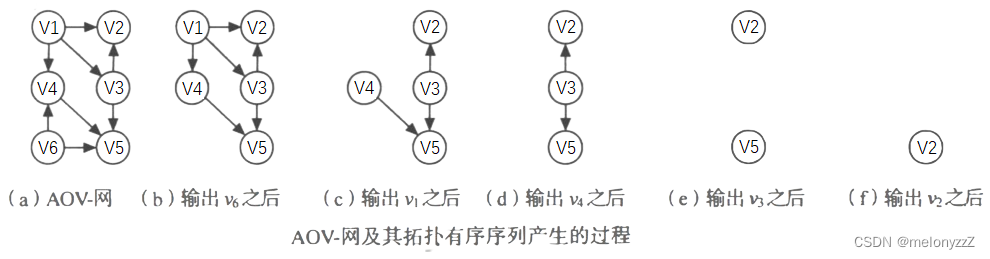
以下图 (a) 中所示的有向图为例,v1 和 v6 没有前驱,则可任选一个。假设先输出 v6,在删除 v6 及弧 <v6, v4>,<v6, v5> 之后,只有顶点 v1 没有前驱,则输出 v1 且删除 v1 及弧 <v1, v2>、<v1, v3> 和 <v1, v4>,之后 v3 和 v4 都没有前驱。依次类推,可从中任选一个继续进行。整个拓扑排序的过程如下图所示,最后得到该有向图的拓扑有序序列为:v6, v1, v4, v3, v2, v5。
三、拓扑排序的实现
针对上述拓扑排序的过程,可采用邻接表做有向图的存储结构。
算法的实现要引入以下辅助的数据结构:
-
一维数组 indegree:存放各顶点入度,没有前驱的顶点就是入度为零的顶点。
-
栈 st:暂存所有入度为零的顶点序号。
删除顶点及以它为尾的弧的操作,可不必真正对图的存储结构进行改变,可以通过栈 st 和对弧头顶点的入度减 1 的办法来实现。
-
一维数组 topo:记录拓扑序列的顶点序号。
算法步骤:
-
求出各顶点的入度存入数组 indegree 中,并将入度为 0 的顶点序号入度。
-
只要栈不空,则重复以下操作:
(1) 将栈顶顶点 vi 的序号出栈,并保存在拓扑序列数组 topo 中;
(2) 对顶点 vi 的每个邻接点 vj 的入度减 1,如果 vj 的入度变为 0,则将 vj 的序号入栈。
-
如果输出顶点个数少于 AOV-网的顶点个数,则网中存在有向环,无法进行拓扑排序,否则拓扑排序成功。
3.1 - ALGraph.h
#pragma once
?
#include <stdbool.h>
?
typedef char VertexType;
?
#define DEFAULT_CAPACITY 2
?
typedef struct ArcNode
{
int adjVexPos;
struct AcrNode* nextArc;
}ArcNode;
?
typedef struct VertexNode
{
VertexType vertex;
ArcNode* firstArc;
}VertexNode;
?
typedef struct ALGraph
{
VertexNode* vertices;
int vSize;
int aSize;
int capacity;
}ALGraph;
?
void ALGraphInit(ALGraph* pg);
?
void ShowAdjList(ALGraph* pg);
?
int GetVertexPos(ALGraph* pg, VertexType v);
?
void InsertVertex(ALGraph* pg, VertexType v);
void InsertArc(ALGraph* pg, VertexType v1, VertexType v2);
?
void ALGraphDestroy(ALGraph* pg);
?
// 拓扑排序
bool TopologicalSort(ALGraph* pg, int* topo);3.2 - ALGraph.c
#include "ALGraph.h"
#include <assert.h>
#include <stdlib.h>
#include <stdio.h>
#include "Stack.h"
?
void ALGraphInit(ALGraph* pg)
{
assert(pg);
pg->vSize = pg->aSize = 0;
pg->capacity = DEFAULT_CAPACITY;
?
pg->vertices = (VertexNode*)malloc(sizeof(VertexNode) * pg->capacity);
assert(pg->vertices);
for (int i = 0; i < pg->capacity; ++i)
{
pg->vertices[i].firstArc = NULL;
}
}
?
void ShowAdjList(ALGraph* pg)
{
assert(pg);
for (int i = 0; i < pg->vSize; ++i)
{
printf("%d %c:>", i, pg->vertices[i].vertex);
ArcNode* cur = pg->vertices[i].firstArc;
while (cur)
{
printf("%d-->", cur->adjVexPos);
cur = cur->nextArc;
}
printf("NULL\n");
}
}
?
int GetVertexPos(ALGraph* pg, VertexType v)
{
assert(pg);
for (int i = 0; i < pg->vSize; ++i)
{
if (pg->vertices[i].vertex == v)
return i;
}
return -1;
}
?
void InsertVertex(ALGraph* pg, VertexType v)
{
assert(pg);
// 考虑是否需要扩容
if (pg->vSize == pg->capacity)
{
VertexNode* tmp = (VertexNode*)realloc(pg->vertices, sizeof(VertexNode) * 2 * pg->capacity);
assert(tmp);
pg->vertices = tmp;
for (int i = pg->capacity; i < 2 * pg->capacity; ++i)
{
pg->vertices[i].firstArc = NULL;
}
pg->capacity *= 2;
}
// 插入顶点
pg->vertices[pg->vSize++].vertex = v;
}
?
void InsertArc(ALGraph* pg, VertexType v1, VertexType v2)
{
assert(pg);
int pos1 = GetVertexPos(pg, v1);
int pos2 = GetVertexPos(pg, v2);
if (pos1 == -1 || pos2 == -1)
return;
// 插入 <v1, v2>
ArcNode* p = (ArcNode*)malloc(sizeof(ArcNode));
assert(p);
p->adjVexPos = pos2;
// 头插
p->nextArc = pg->vertices[pos1].firstArc;
pg->vertices[pos1].firstArc = p;
?
++pg->aSize;
}
?
void ALGraphDestroy(ALGraph* pg)
{
assert(pg);
for (int i = 0; i < pg->vSize; ++i)
{
ArcNode* cur = pg->vertices[i].firstArc;
while (cur)
{
// 头删
pg->vertices[i].firstArc = cur->nextArc;
free(cur);
cur = pg->vertices[i].firstArc;
}
}
free(pg->vertices);
pg->vertices = NULL;
pg->vSize = pg->aSize = pg->capacity = 0;
}
?
// 拓扑排序的实现
bool TopologicalSort(ALGraph* pg, int* topo)
{
assert(pg);
int* indegree = (int*)malloc(sizeof(int) * pg->vSize);
assert(indegree);
for (int i = 0; i < pg->vSize; ++i)
{
indegree[i] = 0;
}
for (int i = 0; i < pg->vSize; ++i)
{
ArcNode* cur = pg->vertices[i].firstArc;
while (cur)
{
++indegree[cur->adjVexPos];
cur = cur->nextArc;
}
}
?
Stack st;
StackInit(&st);
for (int i = 0; i < pg->vSize; ++i)
{
if (indegree[i] == 0)
StackPush(&st, i);
}
?
int cnt = 0;
while (!StackEmpty(&st))
{
int i = StackTop(&st);
StackPop(&st);
topo[cnt++] = i;
?
ArcNode* cur = pg->vertices[i].firstArc;
while (cur)
{
if (--indegree[cur->adjVexPos] == 0)
StackPush(&st, cur->adjVexPos);
cur = cur->nextArc;
}
}
StackDestroy(&st);
?
if (cnt == pg->vSize)
return true;
else
return false;
}3.3 - Test.c
#include "ALGraph.h"
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
?
int main()
{
ALGraph g;
ALGraphInit(&g);
InsertVertex(&g, 'A');
InsertVertex(&g, 'B');
InsertVertex(&g, 'C');
InsertVertex(&g, 'D');
InsertVertex(&g, 'E');
InsertVertex(&g, 'F');
InsertArc(&g, 'A', 'B');
InsertArc(&g, 'A', 'C');
InsertArc(&g, 'A', 'D');
InsertArc(&g, 'C', 'B');
InsertArc(&g, 'C', 'E');
InsertArc(&g, 'D', 'E');
InsertArc(&g, 'F', 'D');
InsertArc(&g, 'F', 'E');
ShowAdjList(&g);
printf("\n");
?
int* topo = (int*)malloc(sizeof(int) * g.vSize);
assert(topo);
if (TopologicalSort(&g, topo))
{
for (int i = 0; i < g.vSize; ++i)
{
printf("%c ", g.vertices[topo[i]].vertex);
}
printf("\n");
}
else
{
printf("网中存在有向环!\n");
}
free(topo);
?
ALGraphDestroy(&g);
return 0;
}
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!