【C++进阶03】二叉搜索树

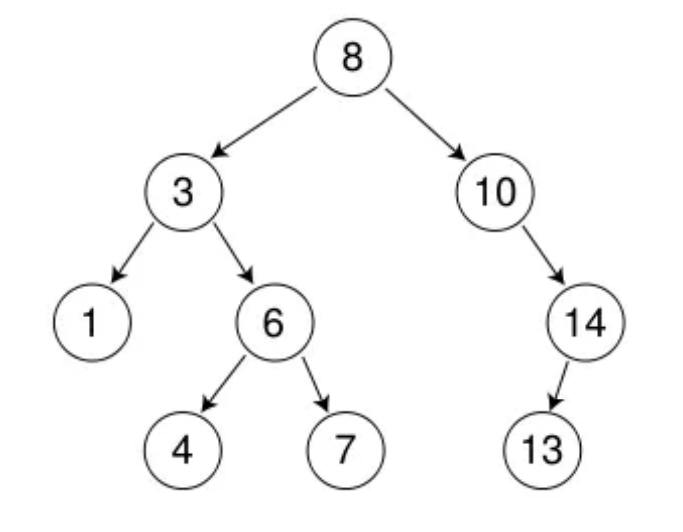
一、二叉搜索树的概念和性质

中序遍历二叉搜索树会得到一个有序序列
所以二叉搜索树又称二叉排序树
它可以是一棵空树
也可以是具有以下性质的二叉树：

• 若它的左子树不为空
则左子树上所有节点的值都小于根节点的值
• 若它的右子树不为空
则右子树上所有节点的值都大于根节点的值
• 它的左右子树也分别为二叉搜索树

二叉搜索树没有相同值的节点
二叉搜索树支持增删查，不支持改
修改会破坏二叉搜索树跟节点比左子树大
右子树小的结构

如图：

二、二叉搜索树的模拟实现

二叉搜索树节点

// BSTree.h
#pragma once

// BinarySearchTree --- BSTree
template<class K>
struct BSTreeNode
{
	BSTreeNode<K>* _left;
	BSTreeNode<K>* _right;
	K _key;

	BSTreeNode(const K& key)
		:_left(nullptr)
		, _right(nullptr)
		, _key(key)
	{}
};

二叉搜索树的插入、中序遍历和查找

template<class K>
class BSTree
{
	typedef BSTreeNode<K> Node; // 名字过长在类里面再typedef，类里受类域限制不会名字冲突
public:
	bool Insert(const K& key) // 要插入节点内容重复，插入失败返回false
	{
		if (_root == nullptr)
		{
			_root = new Node(key); // 没写构造函数会导致无法将参数 1 从“const K”转换为“const BSTreeNode<K> &”，new的时候会以为你要调转换
			return true;
		}

		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key < key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_key > key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				return false;
			}
		}

		cur = new Node(key);
		// 链接
		if (parent->_key < key)
		{
			parent->_right = cur;
		}
		else
		{
			parent->_left = cur;
		}
		
		return true;
	}

	bool Find(const K& key)
	{
		Node* cur = _root;

		while (cur)
		{
			if (cur->_key > key)
			{
				cur = cur->_left;
			}
			else if (cur->_key < key)
			{
				cur = cur->_right;
			}
			else
			{
				return true;
			}
		}
		return false;
	}

	void InOrder() // 中序需要传_root根节点，在类外无法直接访问，所以再套一层。不能用缺省值解决
	{
		_InOrder(_root);
	}

	// void _InOrder(Node* root = _root) // 缺省值必须是全局变量或是常量，访问_root得用this，而this只能在函数内部使用
	void _InOrder(Node* root) // 中序
	{
		if (root == nullptr)
			return;

		_InOrder(root->_left);
		cout << root->_key << " ";
		_InOrder(root->_right);
	}

private:
	Node* _root = nullptr;
};

插入的递归实现

bool _InsertR(Node*& root, const K& key) // 用&解决链接问题，最后走到nullptr的位置是上一个节点的别名，很巧妙的链接上
{
	if (root == nullptr)
	{
		root = new Node(key);
		return true;
	}

	if (root->_key < key)
	{
		return _InsertR(root->_right, key);
	}
	else if (root->_key > key)
	{
		return _InsertR(root->_left, key);
	}
	else
	{
		return false;
	}
}

bool InsertR(const K& key)
{
	return _InsertR(_root, key);
}

查找的递归实现

bool _FindR(Node* root, const K& key) 
{
	if (root == nullptr)
		return false;

	if (root->_key == key)
		return true;

	else if (root->_key < key)
		return _FindR(root->_right, key);
	else
		return _FindR(root->_left, key);

	return false;
}

bool FindR(const K& key) // 递归查找
{
	return _FindR(_root, key);
}

二叉搜索树的难点在于删除
分别有三种情况

1. 被删的节点没有孩子节点
2. 被删的节点只有左孩子或右孩子

第一种情况直接删不用特殊处理
第二种情况将被删节点的孩子节点
连接到他的父节点即可

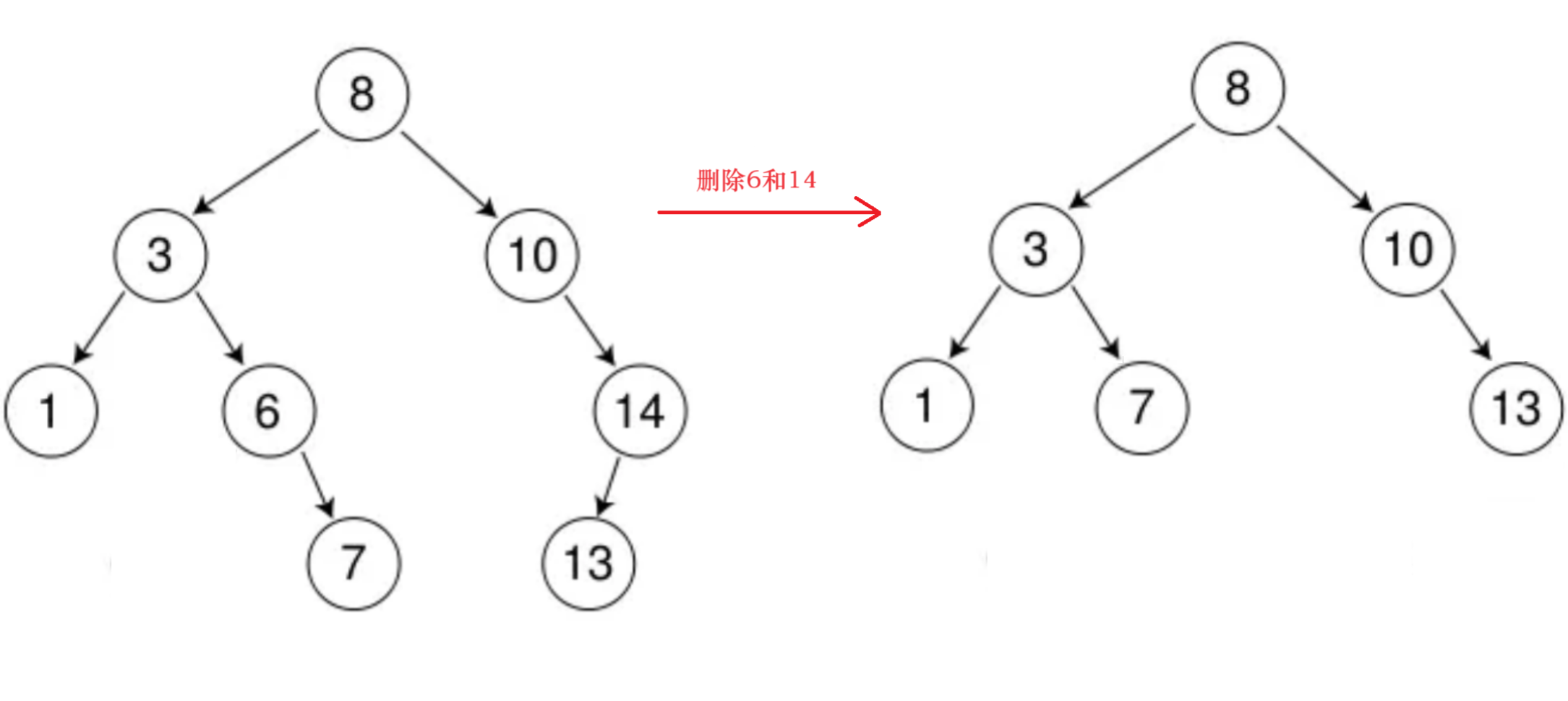
3. 被删的节点有两个孩子节点

这时被删的节点的父节点
无法接管他的两个孩子节点
解决方法：
请一个节点替自己接管自己的两个孩子
这个节点可以是左子树最大的节点 or
右子树最小节点

删除接口代码实现

bool Erase(const K& key)
{
	Node* parent = nullptr;
	Node* cur = _root;

	while (cur)
	{
		if (cur->_key < key)
		{
			parent = cur;
			cur = cur->_right;
		}
		else if (cur->_key > key)
		{
			parent = cur;
			cur = cur->_left;
		}
		else
		{
			// 删除
			// 1. 左为空
			if (cur->_left == nullptr)
			{
				if (cur == _root) // 解决根节点没有父节点的问题
				{
					_root = _root->_right;
				}
				else
				{
					if (parent->_left == cur)
					{
						parent->_left = cur->_right;
					}
					else
					{
						parent->_right = cur->_right;
					}
				}
				delete cur;
			}
			// 2. 右为空
			else if (cur->_right == nullptr)
			{
				if (cur == _root) // 解决根节点没有父节点的问题
				{
					_root = _root->_left;
				}
				else
				{
					if (parent->_left == cur)
					{
						parent->_left = cur->_left;
					}
					else
					{
						parent->_right = cur->_left;
					}
				}
				delete cur;
			}
			// 3. 左右都不为空
			else
			{
				// 找右树最小节点替换被删节点，也可以是左树最大节点
				Node* pMinRight = cur;
				Node* MinRight = cur->_right;
				while (MinRight->_left)
				{
					pMinRight = MinRight;
					MinRight = MinRight->_left;
				}

				cur->_key = MinRight->_key;
				if (pMinRight->_left == MinRight)
				{
					pMinRight->_left = MinRight->_right;
				}
				else
				{
					pMinRight->_right = MinRight->_right;
				}

				delete MinRight;
			}
			return true;  
		}
	}

	return false;
}

删除递归实现

bool _EraseR(Node*& root, const K& key)
{
	if (root == nullptr)
		return false;

	if (root->_key < key)
	{
		return _EraseR(root->_right, key);
	}
	else if (root->_key > key)
	{
		return _EraseR(root->_left, key);
	}
	else
	{
		// 删除节点
		Node* del = root; // 保存要删的节点
		if (root->_right == nullptr)
			root = root->_left;
		else if (root->_left == nullptr)
			root = root->_right;
		else
		{
			Node* MaxLeft = root->_left;
			while (MaxLeft->_right)
			{
				MaxLeft = MaxLeft->_right;
			}

			swap(root->_key, MaxLeft->_key);

			return _EraseR(_root->_left, key); // 转换成子树去删除
		}

		delete del;
		return true;
	}
}

????????
本篇博客完，感谢阅读🌹
如有错误之处可评论指出
博主会耐心听取每条意见
????????