油漆面积（暴力算法 + 扫描线法 + 线段树lazy标记详解）

油漆面积问题

前言

对于求面积问题，尤其是像接下来题目描述的那样多个二维矩形，并且存在重叠情况下的问题，我们往往会感到束手无策，但是，在这里我要为大家介绍一种方法能够帮助大家熟练地解决这类麻烦的题目—扫描线法，同时也会为大家给出暴力解法【当然是为了在比赛过程更好地拿分】，由于该方法还包含线段树的基础与高级应用，在后文当中我也会给出详细的介绍和讲解，喜欢的小伙伴可以点个关注喽。

知识预备

线段树的基本操作

1.线段树构建

2.线段树单点修改

3线段树查询

详见我的另外一篇博客，这里面有保姆级的教程
链接: https://blog.csdn.net/2302_77698668/article/details/132686808

线段树的lazy标记

定义【官方解释】

线段树的lazy标记是一种优化技术，用于延迟更新操作。在线段树中，当需要对某个区间进行更新时，通常需要更新该区间上的所有节点。然而，这样的更新操作可能会导致不必要的重复计算，降低效率。

为了解决这个问题，引入了lazy标记。当进行更新操作时，不立即更新区间的节点，而是将更新操作标记为"lazy"，并将更新的值保存在相应的节点中。只有当需要查询或进一步更新该区间时，才会将lazy标记的更新操作应用到节点上。

通过使用lazy标记，可以减少不必要的节点更新操作，提高线段树的效率。特别是在处理大规模的区间查询问题时，lazy标记可以显著降低时间复杂度。

自定义【图像解释】

线段树在进行修改和查询操作时，会按照递归依次向下搜索，一直检索到叶子结点后返回，这就会造成大量的浪费。
举一个线段树的例子分析，看图
下面是一个线段树

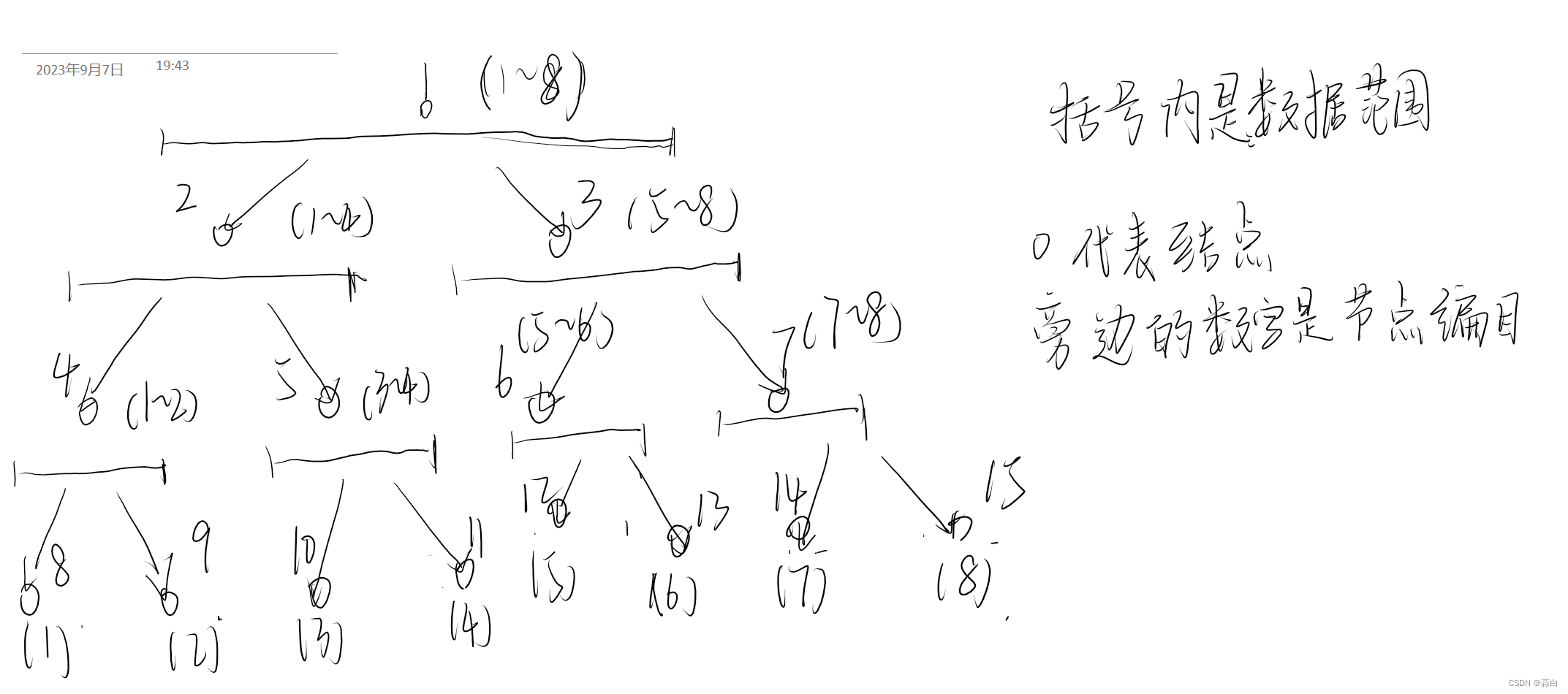
假设要进行多次修改，查询，首先进行对（1~4）进行增加 66 操作
按理来说只要找到 （1~4）区间就可以了，但是线段树的递归性质会造成（1,4）下面的 （1-2）、（3-4）区间发生改变，接着就是 （1） （2）（3）（4）自区间发生改变，这样做是没必要的。
如图

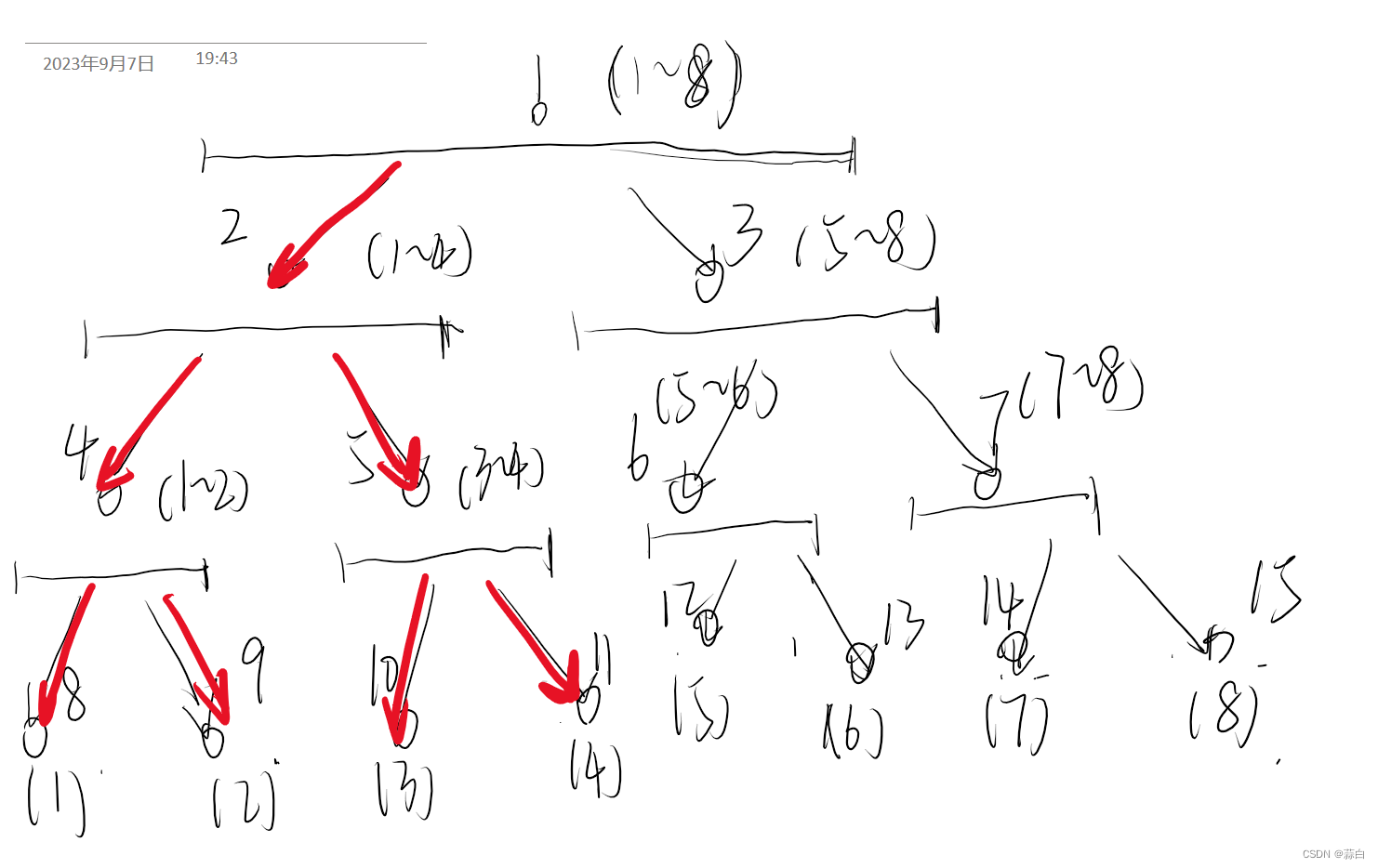
而lazy标记则是可以减少这一不必要操作
使用lazy标记的法则如下：
1.如果修改的区间完全覆盖当前区间，直接更新当前区间，打上lazy标记
2.如果没有完全覆盖，且当前区间有lazy标记，先下传lazy标记到自区间，再清除当前区间lazy标记
3.如果搜索区间和左儿子有交集，则对左儿子进行搜索
4.右儿子的操作同理与左儿子

举例，我们还是按照上面的例子

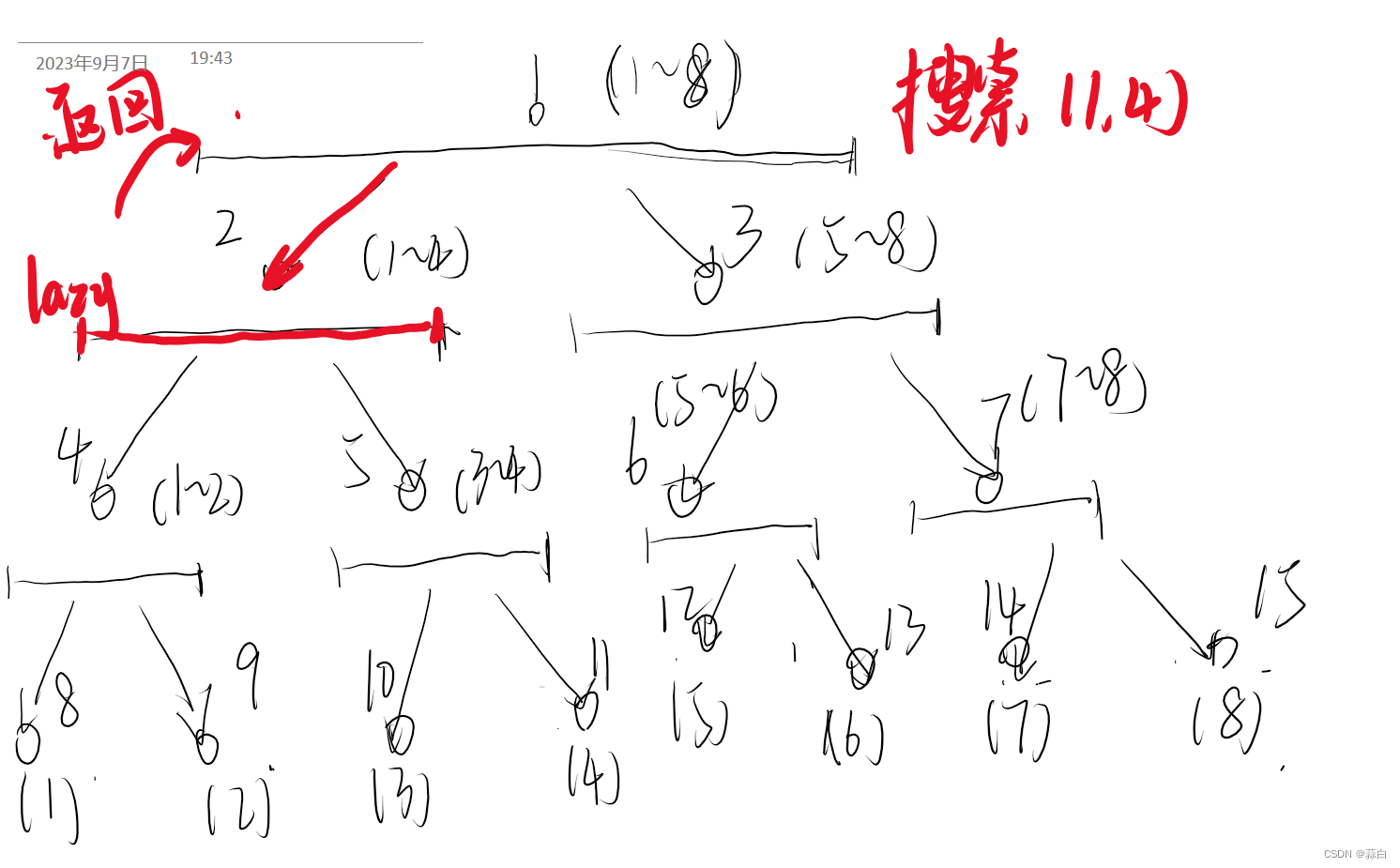
这个例子比较特殊，我们在举一个，看图

struct Node{
    int l,r;//l,r 分别记录节点代表的区间的范围
    int lazy;//这个是lazy标记
    int max;//这里可以是min,max,sum
}

扫描线法介绍

往往我们会遇到求面积的困境，繁杂的坐标，重复的面积，等等、、、
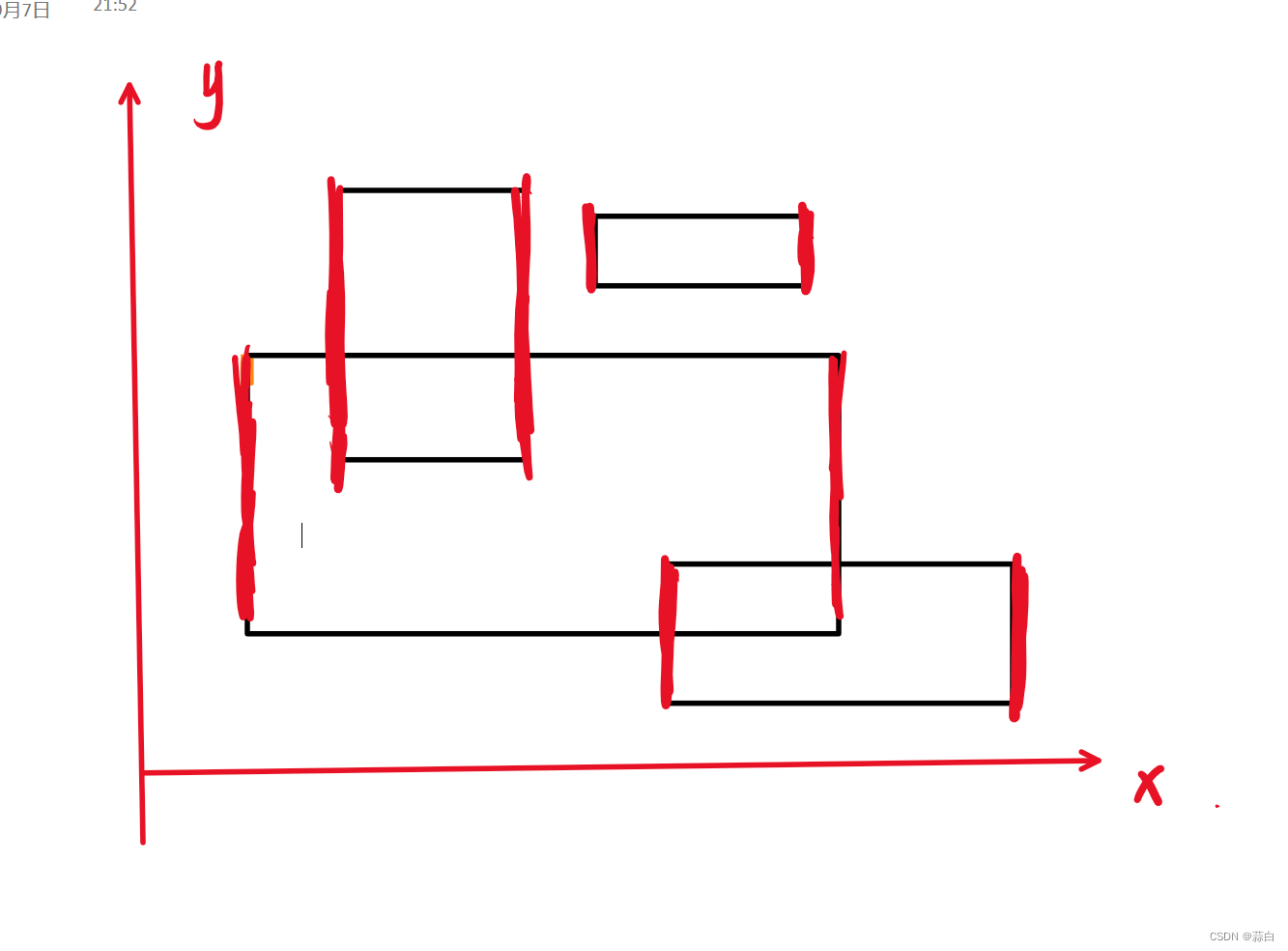
这里就可以体现出扫描线法的作用了，看图

我们将点的横坐标拍好序，就形成了一块有一块的矩形区域，每个区域的宽是
x2-x1 x3-x2 x4-x3
高是相同涂色区域的高的总和，我们以x2--x3 区间为例，看图

那面积自然就好说嘛
各个矩形面积之和即使我们要求的面积
至于这么获取 高，就要用到线段树的知识，这个在下文中会提到

题目详情【正片开始】

X星球的一批考古机器人正在一片废墟上考古。

该区域的地面坚硬如石、平整如镜。管理人员为方便，建立了标准的直角坐标系。
每个机器人都各有特长、身怀绝技。它们感兴趣的内容也不相同。
经过各种测量，每个机器人都会报告一个或多个矩形区域，作为优先考古的区域。
矩形的表示格式为 (x1,y1,x2,y2)，代表矩形的两个对角点坐标。
为了醒目，总部要求对所有机器人选中的矩形区域涂黄色油漆。
小明并不需要当油漆工，只是他需要计算一下，一共要耗费多少油漆。
其实这也不难，只要算出所有矩形覆盖的区域一共有多大面积就可以了。
注意，各个矩形间可能重叠。

输入格式
第一行，一个整数 n，表示有多少个矩形。

接下来的 n行，每行有 4 个整数 x1,y1,x2,y2，空格分开，表示矩形的两个对角顶点标。

输出格式
一行一个整数，表示矩形覆盖的总面积。

数据范围
1≤n≤10000
,
0≤x1,x2,y2,y2≤10000

数据保证 x1<x2 且 y1<y2

输入样例1：
3
1 5 10 10
3 1 20 20
2 7 15 17
输出样例1：
340
输入样例2：
3
5 2 10 6
2 7 12 10
8 1 15 15
输出样例2：
128

暴力解法【快速混分】

由于思路比较简单，需要解释的地方都在注释里面

#include <iostream>
#include <cstring>
using namespace std;
const int N = 10007;
int cnt[N][N];
typedef long long ll;
int main()
{
	int n;
	int a,b,c,d;
	cin >> n;
	//纯暴力做法
	while (n--)
	{
		cin >> a>>b>>c>>d;
		for (int i = a;i < c;i++)
			for (int j = b;j < d;j++)//
			//这里上限一定要小于 d ，不然计划计算的是 2 * 2 矩形
			//实际上是 （2+1）*（2+1）
				cnt[i][j]=1;
	}
	ll ans = 0;
	for (int i = 0;i < N;i++)
		for (int j = 0;j < N;j++)
			ans+=cnt[i][j];
	cout << ans;
}

线段树解法

可能我们有的小伙伴会好奇我们线段树是产生于哪个数组
别急，看图

就是这些成对出现的线段，当然是排好序的，不够具体，再看图

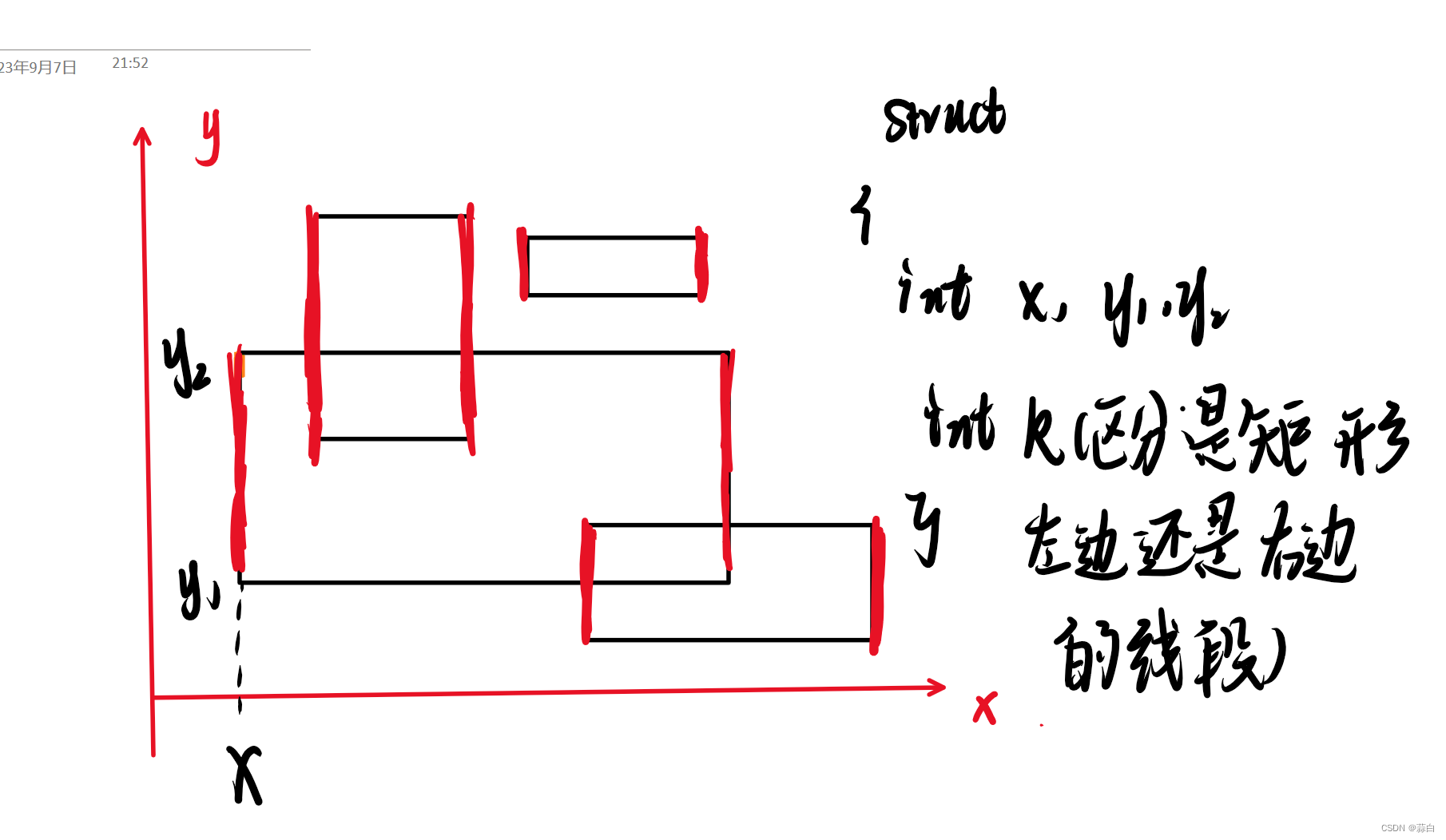
代码如下：

struct Segment
{
    int x, y1, y2;
    int k;
    bool operator< (const Segment &t)const
    //此处的重载体是为了让数组按 x 的大小正序排序
    {
        return x < t.x;
    }
}seg[N * 2];//这里开 2 * N 是因为每个矩形有两条边

接下来是线段树的代码
cnt 代表区间被覆盖的次数，也就是我们的lazy标记

struct Node
{
    int l, r;
    int cnt, len;
    //cnt 代表区间被覆盖的次数，**也就是我们的lazy标记**
    //len 代表的就是区间的高度
}tr[N * 4];

这里的线段树是竖着看的，如图：

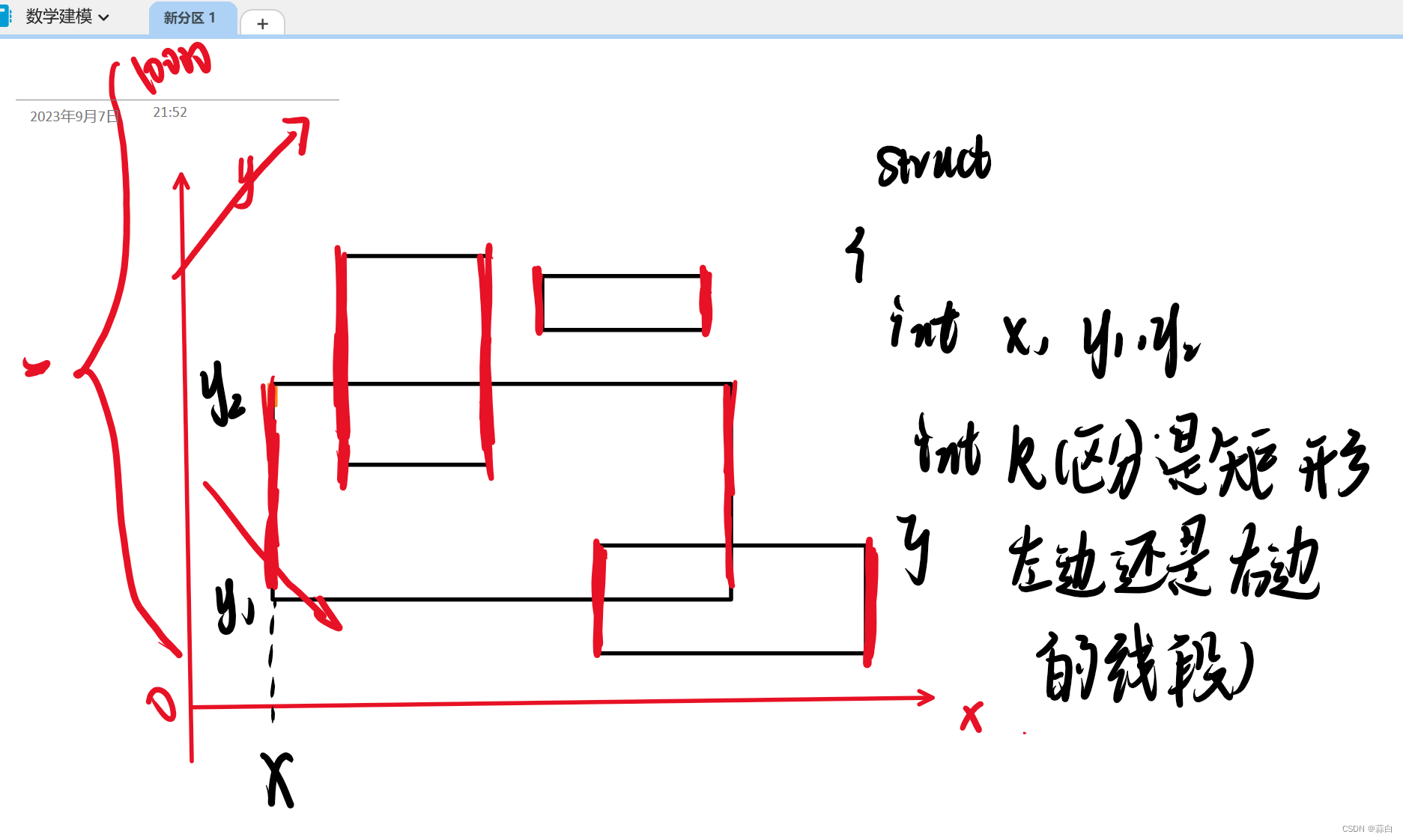
接着是如何用子节点更新父节点的操作，这也是题目的核心代码所在
每次更新的时候要观察根节点此时的覆盖次数 cnt 是否 >=0 ,因为 只有先出现矩形的左边区间，才会出现矩形的右边区间，所以cnt 一定大于等于 0，具体解释在代码注释里面，这样更容易理解
注意看

void pushup(int u)
{
    if (tr[u].cnt > 0) tr[u].len = tr[u].r - tr[u].l + 1;
    //只有当cnt >0 时,我们才可以开始
    //如果 cnt==0 ，没有lazy标记，转为下面的对左儿子，右儿子分析
    else if (tr[u].l == tr[u].r) tr[u].len = 0;
    else tr[u].len = tr[u << 1].len + tr[u << 1 | 1].len;
}

这里并没有对父节点进行更新，为什么呢？
我们将扫描线看出一根固定不动的线，后面的矩形【排好顺序的】从右往左移动，依次经过扫描线，过去的就过去了，不会影响后面的，这就是扫描线的奇特之处，
push操作只对后面的子节点负责更新
除此之外，后面的面积总和计算，我们始终采用的是根节点的len，这也是我为什么将扫描线比作固定不动的一根线的原因，

void modify(int u, int l, int r, int k)
{
    if (tr[u].l >= l && tr[u].r <= r)
    {
        tr[u].cnt += k;//当查询区间完全覆盖当前区间的时候
        //我们打上lazy标记
        pushup(u);//每次对叶子结点更新完之后需要对后面的节点更新
    }
    //--------------------
    //下面和寻常线段树操作一样
    else
    {
        int mid = tr[u].l + tr[u].r >> 1;
        if (l <= mid) modify(u << 1, l, r, k);
        if (r > mid) modify(u << 1 | 1, l, r, k);
        pushup(u);
    }
}

代码：

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 10010;

int n;
struct Segment
{
    int x, y1, y2;
    int k;
    bool operator< (const Segment &t)const
    {
        return x < t.x;
    }
}seg[N * 2];
struct Node
{
    int l, r;
    int cnt, len;
}tr[N * 4];

void pushup(int u)
{
    if (tr[u].cnt > 0) tr[u].len = tr[u].r - tr[u].l + 1;
    else if (tr[u].l == tr[u].r) tr[u].len = 0;
    else tr[u].len = tr[u << 1].len + tr[u << 1 | 1].len;
}

void build(int u, int l, int r)
{
    tr[u] = {l, r};
    if (l == r) return;
    int mid = l + r >> 1;
    build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
}

void modify(int u, int l, int r, int k)
{
    if (tr[u].l >= l && tr[u].r <= r)
    {
        tr[u].cnt += k;
        pushup(u);
    }
    else
    {
        int mid = tr[u].l + tr[u].r >> 1;
        if (l <= mid) modify(u << 1, l, r, k);
        if (r > mid) modify(u << 1 | 1, l, r, k);
        pushup(u);
    }
}

int main()
{
    scanf("%d", &n);
    int m = 0;
    for (int i = 0; i < n; i ++ )
    {
        int x1, y1, x2, y2;
        scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
        seg[m ++ ] = {x1, y1, y2, 1};
        seg[m ++ ] = {x2, y1, y2, -1};
        //这里的 + 1  - 1 代表的是矩形左边和右边 
    }

    sort(seg, seg + m);

    build(1, 0, 10000);

    int res = 0;
    for (int i = 0; i < m; i ++ )
    {
        if (i > 0) res += tr[1].len * (seg[i].x - seg[i - 1].x);
        //每次计算总和之后在添加新的数
        modify(1, seg[i].y1, seg[i].y2 - 1, seg[i].k);
        //这里维护的是一段区间，之所以seg[i].y2 - 1
        //是因为避免重复现象
        //因为是靠点取维护区间
        //比如说区间【2,3】对应的节点是2
    }

    printf("%d\n", res);

    return 0;
}