大数据HCIE成神之路之数据预处理（2）——异常值处理

2023-12-17 15:58:25

1 异常值处理

1.1 散点图

将数据用散点图的形式可视化呈现，以便观察到数据集中的异常值。

Python中 matplotlib.pyplot 库的 scatter 函数用于数据集的可视化输出。其基本格式如下：

scatter(x, y, s=None, c=None, marker=None, cmap=None, norm=None, vmin=None, vmax=None, alpha=None, linewidths=None, verts=None, edgecolors=None, hold=None, data=None, **kwargs)

关键参数详解：

X代表散点图的x轴数据。
y代表散点图的y轴数据。
s可选参数，代表散点图的数据 大小 。
c可选参数，代表散点图的数据 颜色 ，默认为蓝色。
marker可选参数，代表散点图的 形状 ，默认为○型。
camp可选参数，代表指定 色图 ，默认为None。只有当参数C为浮点型数组时，camp参数才有效。
norm可选参数，代表数据 亮度 ，默认为None。只有当参数C为浮点型数组时，norm参数才有效。
vmin&vmax可选参数，与norm类似，若已使用norm参数，则此参数无效。
alpha可选参数，代表数据 透明度 ，默认为None。数值在0至1之间，0代表透明，1代表不透明。
linewidths可选参数，代表散点图边界线宽度 ，默认为None。
verts可选参数，代表序列[x,y]。如果参数marker为None，则此参数发挥作用 (作用与marker类似)。
edgecolors可选参数，代表散点图边界 颜色 ，默认为‘face’。

1.1.1 实验任务

1.1.1.1 实验背景

通过输出散点图，展示图中的异常值，加深此方法的理解。

1.1.1.2 实验目标

使用pyplot函数可视化数据集，观测异常值。

1.1.1.3 实验数据解析

实验使用的是鸢尾花数据集。

1.1.2 实验思路

使用散点图可视化数据集，查看异常点：

导入实验数据集。
利用 matplotlib.pyplot 函数库输出散点图。

1.1.3 实验操作步骤

步骤 1 数据导入

#导入pandas库和numpy库
import pandas as pd
import numpy as np
# 导入iris数据集
from sklearn.datasets import load_iris
iris=load_iris()
iris.target_names

输出结果：

array(['setosa', 'versicolor', 'virginica'], dtype='<U10')

解释：dtype=‘<U10’ 表示该数组的数据类型是 Unicode 字符串，每个字符串的最大长度为 10 个字符。其中 <U 表示 Unicode 字符串，而 10 表示字符串的最大长度。

在这个例子中，dtype=‘<U10’ 表示每个字符串的最大长度为 10 个字符。如果字符串的长度超过 10，它们将被截断以适应这个长度。这在鸢尾花数据集中是合理的，因为每个类别的名称都不会超过 10 个字符，所以使用这个数据类型的数组可以有效地存储和表示类别名称。

步骤 2 数据可视化

# 导入 matplotlib.pyplot 函数库
import matplotlib.pyplot as plt
# 画散点图，其中第一维数据为 x 轴，第二维数据为 y 轴
# Sepal.Length（花萼长度，特征的第一列）为 x 轴
x_index=0
# Sepal.Width（花萼宽度，特征的第二列）为 y 轴
y_index=1
# 设置数据集颜色，因为数据集分为三类，因此设置成蓝、红和绿三色。
colors = ['blue', 'red', 'green']
# 先使用 zip 函数将鸢尾花卉种类和颜色打包成元组形式，如[('setosa', 'blue'),('versicolor', 'red'), ('virginica', 'green')]
# 然后使用 for…in…循环，可视化三种数据。
for label, color in zip(range(len(iris.target_names)), colors):
	plt.scatter(iris.data[iris.target == label, x_index], iris.data[iris.target == label, y_index], label=iris.target_names[label], c=color)

解释：

当我们进入for循环时，我们将遍历每个类别的鸢尾花数据，并使用不同的颜色来可视化它们。

label：在每次迭代中，label代表当前类别的索引。它的取值范围是0到2，对应着鸢尾花数据集中的三个类别（是数据集决定的）：setosa（山鸢尾）、versicolor（杂色鸢尾）和virginica（维吉尼亚鸢尾）。
color：在每次迭代中，color代表当前类别的颜色。colors列表中定义了三个颜色：‘blue’（蓝色），‘red’（红色）和’green’（绿色）。zip函数将类别的索引和颜色打包成元组的形式，以便在每次迭代中同时访问它们。
iris.data[iris.target == label, x_index]：这是一个 NumPy 数组的索引操作。iris.data是鸢尾花数据集中的特征数据，iris.target是对应的目标变量。iris.target == label是一个布尔数组，它的值为True或False，用于指示目标变量 是否等于当前的类别索引 。通过这个布尔数组，我们可以筛选出属于当前类别的特征数据。x_index表示我们希望在散点图中使用特征数据的哪个维度作为 x 轴。
iris.data[iris.target == label, y_index]：类似于前面的操作，这里是选择特征数据的另一个维度作为 y 轴。
label=iris.target_names[label]：这是为散点图中每个类别的数据添加标签。iris.target_names是鸢尾花数据集中目标变量的类别名称数组。通过label索引，我们可以获取当前类别的名称，并将其作为标签显示在散点图中。
c=color：这是为散点图中每个类别的数据设置颜色。c参数用于指定散点的颜色，而color变量则是当前类别对应的颜色。

综上所述，该for循环遍历了鸢尾花数据集中的每个类别，根据类别的索引选择相应的特征数据作为 x 轴和 y 轴，并使用不同的颜色和标签将它们可视化成散点图。这样可以直观地展示不同类别之间在两个特征维度上的分布情况。

输出结果如下：
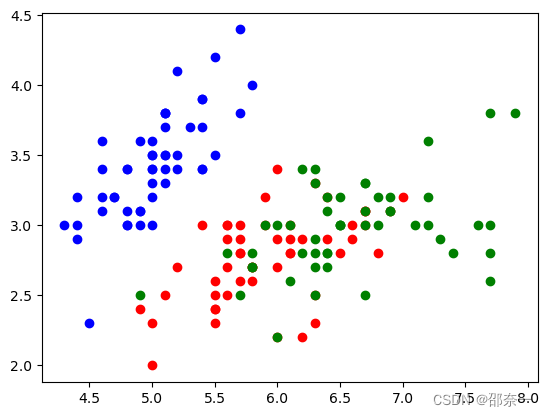
在这里插入图片描述
补充学习一：

zip() 函数非常有用。它会返回一个由元组组成的迭代器，每个元组中包含来自输入可迭代对象的对应元素。

names = ['Alice', 'Bob', 'Charlie']
ages = [25, 30, 35]

for name, age in zip(names, ages):
    print(name, age)

输出结果：

Alice 25
Bob 30
Charlie 35

补充学习二：
假设我们有以下数据：

iris.data = [[5.1, 3.5, 1.4, 0.2],
             [4.9, 3.0, 1.4, 0.2],
             [6.2, 2.9, 4.3, 1.3],
             [5.5, 2.4, 3.8, 1.1],
             [6.3, 3.3, 6.0, 2.5]]
             
iris.target = [0, 0, 1, 1, 2]

iris.data是一个二维数组，表示鸢尾花的特征数据（分别为： 花萼长度，花萼宽度，花瓣长度，花瓣宽度 ）。每一行代表一个样本，每一列代表一个特征。 iris.target 是一个一维数组，表示对应样本的类别标签。

现在，我们来解释 iris.data[iris.target == label, x_index] 这个表达式，假设label为1，x_index为2。

iris.target == label：这是一个布尔数组，它的长度与iris.target相同。它的值为True或False，表示对应位置的样本是否属于label所代表的类别。在我们的例子中，iris.target == label的结果为[False, False, True, True, False]。
iris.data[iris.target == label]：这是一个数组索引操作，它使用布尔数组iris.target == label作为索引， 从iris.data中筛选出对应位置为True的行 。在我们的例子中，这个表达式的结果是一个二维数组：

[[6.2, 2.9, 4.3, 1.3],
 [5.5, 2.4, 3.8, 1.1]]

iris.data[iris.target == label, x_index]：这是一个二维数组的索引操作，它使用布尔数组iris.target == label筛选出的行，并选择其中的第x_index列（ 此处为2，即第3列 ）作为结果。在我们的例子中，这个表达式的结果是一个一维数组：

[4.3, 3.8]

所以， iris.data[iris.target == label, x_index] 的意思是，从iris.data中选择属于label类别的样本，并且只保留这些样本的第x_index个特征值。

1.1.4 结果验证

从图中可以得到，对于左上方数据点集群 (setosa，蓝圆点) 来说，左下角的蓝圆点离setosa数据集群较远，可将其认为异常值。

1.2 基于分类模型的异常检测

本实验以决策树模型为例。

Python的 sklearn.tree 库中的 DecisionTreeClassifier 函数可进决策树建模和预测，以便进行数异常检测。其基本格式如下：

DecisionTreeClassifier(criterion='gini', splitter='best', max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=None, random_state=None, max_leaf_nodes=None, min_impurity_decrease=0.0, min_impurity_split=None, class_weight=None, presort=False)

关键参数详解：

criterion可选参数，代表特征选择标准，criterion=gini为 基尼系数 ，criterion=entropy为 信息增益 。默认为gini。
splitter可选参数，代表特征划分点选择标准，splitter=best为针对所有特征找出最优的特征划分点，splitter=random为随机的在部分特征中找局部最优的划分点。默认为best，适用于小样本数据，若数据量过大，则random较为合适。
max_depth可选参数，代表树的最大深度，max_depth=None为不限制树的深度，适用于小样本数据。若数据量过大，则需设置树的最大深度，10-100较为合理。默认为None。
min_samples_split可选参数，代表内部节点划分所需最小样本数。若某节点的样本数少于min_samples_split，则停止继续选择最优特征划分。默认为2。
min_samples_leaf可选参数，代表叶子节点最少样本数，默认值1。
min_weight_fraction_leaf可选参数，代表叶子节点最小的样本权重和。若样本有较多缺失值，则引入样本权重。默认为0，不考虑权重问题。
max_features可选参数，代表划分时的最大特征数。若为log2则划分时最多考虑log2(n_features)个特征；若为sqrt或auto则划分时最多考虑sqrt(n_features)个特征。默认为None。
max_leaf_nodes可选参数，代表构建树时的最大叶子节点数量。默认为None。
presort可选参数，Boolean，代表数据是否排序。数据量较小时，对数据排序可加快建模速度。默认为False。

1.2.1 实验任务

1.2.1.1 实验背景

利用分类算法将数据集分类，加深此方法的理解。

1.2.1.2 实验目标

使用分类模型判断数据A和B是否异常。

1.2.1.3 实验数据解析

实验使用的是鸢尾花数据集。

1.2.2 实验思路

使用分类模型 (tree模型) 进行异常值检测：

导入实验数据集。
生成实验测试集。
利用实验数据集进行回归建模。
利用建好的回归模型，对实验测试集中的缺失值进行预测。

1.2.3 实验操作步骤

测试数据如下。

“sepal length (cm)”:[5.6,4.9]，
“sepal width (cm)”:[2.5,3]，
“petal length (cm)”:[4.5,1.4]，
“petal width (cm)”:[0.2,2.1]。
“targets”:[1,2]。

异常值检测数据集，如下：

Index	sepal length (cm)	sepal width (cm)	petal length (cm)	petal width (cm)	Y
A	5.6	2.5	4.5	0.2	1
B	4.9	3.0	1.4	2.1	2

步骤 1 导入数据集

# 导入 pandas 库和 numpy 库
import pandas as pd
import numpy as np
# 导入数据集 iris
from sklearn.datasets import load_iris
iris = load_iris()
# 导入 iris 数据集，自变量 X 命名为 dfx，分类变量 Y 命名为 dfy。
dfx = pd.DataFrame(data=iris.data, columns=iris.feature_names)
dfx

输出结果如下：
在这里插入图片描述

# 部分关键数据展示
dfy=pd.DataFrame(data=iris.target)
dfy

输出结果：

步骤 2 生成测试集

因iris无缺失值，因此人为生成测试集x_test，来利用决策树模型进行异常检测。

x_test = pd.DataFrame({"sepal length (cm)": [5.6, 4.9],
                       "sepal width (cm)": [2.5, 3],
                       "petal length (cm)": [4.5, 1.4],
                       "petal width (cm)": [0.2, 2.1]})

步骤 3 建立DecisionTreeClassifier模型

# 导入 DecisionTreeClassifier
from sklearn.tree import DecisionTreeClassifier
modelcart = DecisionTreeClassifier()
modelcart.fit(dfx,dfy)

输出结果如下：

DecisionTreeClassifier()

步骤 4 判断数据A和B是否为异常值

# 使用建立好的 tree 模型检验数据点 A 和 B 是否正确
predicted = modelcart.predict(x_test)
predicted

输出结果如下：

array([1, 0])

1.2.4 结果验证

步骤四对实验结果进行了验证，正确检测出异常值。根据决策树模型识别出A理论上应为类别1 (测试数据中A为类别1)；B理论上应为类别2 (测试数据中B为类别0)。因此数据A不是异常值，B是异常值。

1.3 3σ原则

3σ原则 又称为 拉依达准则 ，先假设一组检测数据只含有随机误差，对原始数据进行计算处理得到标准差，然后按一定的概率确定一个区间，认为误差超过这个区间的就属于异常值。一般其值与平均值的偏差绝对值超过三倍标准差的值，则为异常值，需删除。

解释：

3σ原则（Three Sigma Rule），也称为 3倍标准差原则 ，是统计学中的一个概念，用于描述 正态分布 （或近似正态分布）中观测值离均值的距离。

根据3σ原则，对于一个符合正态分布的数据集，大约有：

68% 的观测值落在均值的一个标准差范围内；
95% 的观测值落在均值的两个标准差范围内；
99.7% 的观测值落在均值的三个标准差范围内。
这个原则可以用来判断一个观测值是否异常或离群。如果一个观测值距离均值超过三个标准差，那么可以认为它是一个异常值或离群点。

3σ原则在质量管理、过程控制和数据分析等领域得到广泛应用。它可以帮助识别潜在的问题、异常情况或变化，并指导决策和改进措施。然而，需要注意的是，3σ原则是基于 正态分布 假设的，如果数据不满足正态分布，应谨慎使用该原则。

1.3.1 实验任务

1.3.1.1 实验背景

利用3σ原则发现数据集中的异常值，加深此方法的理解。

1.3.1.2 实验目标

使用3σ原则发现数据集中的异常值。

1.3.1.3 实验数据解析

使用鸢尾花数据集。

1.3.2 实验思路

使用3σ原则发现数据集中异常值：

导入实验数据集。
根据3σ原则的公式计算出异常值。

1.3.3 实验操作步骤

步骤 1 导入数据集

iris是150*4的数据集，为实验过程更易被理解。特取其中一个属性进行3σ原则实验。本实验选取iris数据集中的第一维数据 sepal length (cm) 。

# 选取第一维数据 sepal length (cm)，记为数据集 X
from sklearn.datasets import load_iris
iris=load_iris()
X=iris.data[:,1]
X

输出结果如下：

# 部分关键数据展示
array([3.5, 3. , 3.2, 3.1, 3.6, 3.9, 3.4, 3.4, 2.9, 3.1, 3.7, 3.4, 3. ,
?       3. , 4. , 4.4, 3.9, 3.5, 3.8, 3.8, 3.4, 3.7, 3.6, 3.3, 3.4, 3. ,
?       3.4, 3.5, 3.4, 3.2, 3.1, 3.4, 4.1, 4.2, 3.1, 3.2, 3.5, 3.1, 3. ,
?       3.4, 3.5, 2.3, 3.2, 3.5, 3.8, 3. , 3.8, 3.2, 3.7, 3.3, 3.2, 3.2,
?       3.1, 2.3, 2.8, 2.8, 3.3, 2.4, 2.9, 2.7, 2. , 3. , 2.2, 2.9, 2.9,
?       3.1, 3. , 2.7, 2.2, 2.5, 3.2, 2.8, 2.5, 2.8, 2.9, 3. , 2.8, 3. ,

补充解释：
iris.data[:,1] 是二位数组，举例：

import numpy as np
ar1=np.arange(12).reshape((4, 3))
ar1

array([[ 0,  1,  2],
       [ 3,  4,  5],
       [ 6,  7,  8],
       [ 9, 10, 11]])

获取二维数组的第一列：

ar1[:,0]

输出结果为：

array([0, 3, 6, 9])

获取二维数组的第二列：

ar1[:,1]

输出结果为：

array([1, 4, 7, 10])

输出前两行的第一列：

ar1[:2,0]

输出结果为：

array([0, 3])

步骤 2 计算数据集的均值

# 导入 numpy 库，可计算均值和标准差
import numpy as np
mean=np.mean(X)
mean

输出结果如下：

3.0573333333333337

步骤 3 计算数据集的标准差和三倍标准差

# 计算数据集 X 的标准差
standard=np.std(X)
standard

输出结果如下：

0.4321465800705435

计算三倍标准差：

b=3*standard
b

输出结果如下：

1.3032329032064838

步骤 4 计算数据集X与平均值的偏差的绝对值

a=abs(X-mean)
a

输出结果如下：

# 部分关键数据展示
array([0.44266667, 0.05733333, 0.14266667, 0.04266667, 0.54266667,
       0.84266667, 0.34266667, 0.34266667, 0.15733333, 0.04266667,
       0.64266667, 0.34266667, 0.05733333, 0.05733333, 0.94266667,
       1.34266667, 0.84266667, 0.44266667, 0.74266667, 0.74266667,
       0.34266667, 0.64266667, 0.54266667, 0.24266667, 0.34266667,
       0.05733333, 0.34266667, 0.44266667, 0.34266667, 0.14266667,
       0.04266667, 0.34266667, 1.04266667, 1.14266667, 0.04266667,
       0.14266667, 0.44266667, 0.54266667, 0.05733333, 0.34266667,
       0.44266667, 0.75733333, 0.14266667, 0.44266667, 0.74266667,
       0.05733333, 0.74266667, 0.14266667, 0.64266667, 0.24266667,

步骤 5 判断异常值

计算数据集X与平均值的偏差绝对值是否超过三倍标准差，并输出异常值。

# 利用 for 循环将数据集 X 的偏差绝对值依次与三倍标准差对比，超过则为异常值并输出异常值。
for i in range(1, 150):
	if a[i] > b:
		print('当前异常值为 :', a[i])
		print('当前异常值位置为 :', i)

输出结果如下：

当前异常值为 : 1.3426666666666667
当前异常值位置为 : 15

1.3.4 结果验证

经实验发现，第一维 sepal length (cm) 的第15个数据为异常值，因为其与平均值的偏差的绝对值超多三倍标准差。

对于小样本数据集，3σ原则可能不太适用。在小样本情况下，由于数据点较少，计算均值和标准差可能会受到极端值或离群点的影响，从而导致均值和标准差的估计不准确。

此外，如果数据集不符合正态分布假设，即使数据量很大，也应该谨慎使用3σ原则。在非正态分布的情况下，数据点的分布可能不服从均值加减3倍标准差的规律。

1.4 箱型图分析

箱线图依据实际数据绘制，其判断异常值的标准以四分位数和四分位距为基础，分为上四分位、下四分位、IQR，由此计算出最大估计值和最小估计值。其基本格式如下：

DataFrame.describe()

此函数输出得到如下结果。

输出详解：

Count代表数据集数量。
Mean代表数据集均值。
Std代表数据集标准差。
Min代表数据集最小值。
25%代表数据集中25%分位数据。
50%代表数据集中50%分位数据。
75%代表数据集中75%分位数据。
max代表数据集最大值。

1.4.1 实验任务

1.4.1.1 实验背景

利用箱型图发现数据集中的异常值，加深此方法的理解。

1.4.1.2 实验目标

通过箱型图检测预测值，并输出异常值。

1.4.2 实验思路

使用箱型图检测数据集中的异常值：

导入实验数据集。
根据箱型图计算出异常值。

1.4.3 实验操作步骤

步骤 1 导入数据和函数库

iris是150*4的数据集，为实验过程更易被理解。特取其中一个属性进行3σ原则实验。本实验选取数据集中的第二维 sepal width (cm) （可以尝试用第一个维度看有面试结果【无异常值】）。

# 导入 pandas 和 matplotlib 库
import matplotlib.pyplot as plt
import pandas as pd
from sklearn import datasets
iris = datasets.load_iris()
statistics=iris.data[:,1]
statistics

输出结果如下：

# 数据展示
array([3.5, 3. , 3.2, 3.1, 3.6, 3.9, 3.4, 3.4, 2.9, 3.1, 3.7, 3.4, 3. ,
       3. , 4. , 4.4, 3.9, 3.5, 3.8, 3.8, 3.4, 3.7, 3.6, 3.3, 3.4, 3. ,
       3.4, 3.5, 3.4, 3.2, 3.1, 3.4, 4.1, 4.2, 3.1, 3.2, 3.5, 3.6, 3. ,
       3.4, 3.5, 2.3, 3.2, 3.5, 3.8, 3. , 3.8, 3.2, 3.7, 3.3, 3.2, 3.2,
       3.1, 2.3, 2.8, 2.8, 3.3, 2.4, 2.9, 2.7, 2. , 3. , 2.2, 2.9, 2.9,
       3.1, 3. , 2.7, 2.2, 2.5, 3.2, 2.8, 2.5, 2.8, 2.9, 3. , 2.8, 3. ,
       2.9, 2.6, 2.4, 2.4, 2.7, 2.7, 3. , 3.4, 3.1, 2.3, 3. , 2.5, 2.6,
       3. , 2.6, 2.3, 2.7, 3. , 2.9, 2.9, 2.5, 2.8, 3.3, 2.7, 3. , 2.9,
       3. , 3. , 2.5, 2.9, 2.5, 3.6, 3.2, 2.7, 3. , 2.5, 2.8, 3.2, 3. ,
       3.8, 2.6, 2.2, 3.2, 2.8, 2.8, 2.7, 3.3, 3.2, 2.8, 3. , 2.8, 3. ,
       2.8, 3.8, 2.8, 2.8, 2.6, 3. , 3.4, 3.1, 3. , 3.1, 3.1, 3.1, 2.7,
       3.2, 3.3, 3. , 2.5, 3. , 3.4, 3. ])

步骤 2 利用 describe () 得到25%分位数据、75%分位数据

# describe()适用于 DataFrame 结构的数据，因此把 statistics 转化成 DataFrame结构
statistics=pd.DataFrame(statistics)
c=statistics.describe()
c

输出结果如下：


		0
count	150.000000
mean	3.057333
std		0.435866
min		2.000000
25%		2.800000
50%		3.000000
75%		3.300000
max		4.400000

思考：什么叫什么是25% 分位数（25%）、中位数（50%）、75% 分位数（75%）？
回答：

25%分位数（第一四分位数）：它将数据集划分为四个等份之一，并表示数据集中的25%的观测值位于该值以下。换句话说， 25%分位数是将数据集从小到大排序后，位于25%位置的值。有时也被称为下四分位数（Lower Quartile） 。
中位数（第二四分位数）：它将数据集划分为两个等份，即中间位置。中位数表示数据集中的50%的观测值位于该值以下。如果数据集中的观测值个数为奇数，则中位数是中间的值；如果观测值个数为偶数，则中位数是中间两个值的平均值。
75%分位数（第三四分位数）：它将数据集划分为四个等份之一，并表示数据集中的75%的观测值位于该值以下。换句话说，75%分位数是将数据集从小到大排序后，位于75%位置的值。有时也被称为上四分位数（Upper Quartile）。

步骤 3 计算IQR

IQR=c.loc['75%']-c.loc['25%']
IQR

思考：IQR是什么意思？
IQR（Interquartile Range）是数据集中的一个统计量，表示75%分位数与25%分位数之间的距离。

IQR的计算可以提供关于数据集中间50%的离散程度的信息。它衡量了数据集中离散值的范围，即数据集中的中间50%观测值的离散程度。 较大的IQR值表示数据的离散程度较大，而较小的IQR值表示数据的离散程度较小 。

在实际应用中，IQR常用于识别数据集中的离群值（异常值）。根据常用的经验法则，可以将超过1.5倍IQR的值定义为潜在的离群值。 通过计算IQR并结合其他方法，可以帮助识别和处理数据集中的异常值，从而提高数据分析的准确性和可靠性。

输出结果：

0    0.5
dtype: float64

解释：输出的IQR值为0.5，这意味着，在这个特征上，数据的分布相对较紧密，观测值之间的差异较小。

步骤 4 计算最大预估值和最小预估值

# 最大预估值为8.35
maxCount=c.loc['75%']+1.5*IQR
maxCount

输出结果如下：

0    4.05
dtype: float64

解释：根据输出结果，最大预估值为4.05。这个结果告诉你，在这个特定的特征上，超过4.05的观测值可以被视为潜在的离群值。 超过这个值的观测值可能是相对较远离数据集中心的异常值。

# 最小预估值为 2.05
minCount=c.loc['25%']-1.5*IQR
minCount

输出结果如下：

0    2.05
dtype: float64

解释：在这个特定的特征上，小于2.05的观测值可以被视为潜在的离群值。 小于这个值的观测值可能是相对较远离数据集中心的异常值。通过计算最大预估值和最小预估值，你可以得到一个范围，在这个范围之外的观测值可能被认为是潜在的离群值。

步骤 5 验证数据集中是否有异常值，并输出异常值

# 取出 iris 第二维数据循环输出异常值。
X = iris.data[:, 0]
for i in range(1, 150):
	if X[i] > maxCount.values or X[i] < minCount.values:
		print('当前异常值为 :', X[i])
		print('当前异常值位置为 :', i)

部分输出结果如下：

当前异常值为 : 4.4
当前异常值位置为 : 15
当前异常值为 : 4.1
当前异常值位置为 : 32
当前异常值为 : 4.2
当前异常值位置为 : 33
当前异常值为 : 2.0
当前异常值位置为 : 60

for循环结构不适用于DataFrame结构的数据， describe() 要求数据为DataFrame结构，因此statistic数据集不适用于for循环。在此实验中，使用原始数据集X进行for循环输出。

步骤 6 可视化验证分析结果是否准确

plt.figure()
plt.boxplot(statistics)
plt.show()

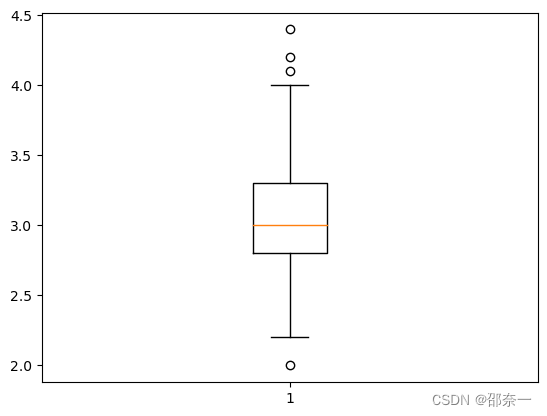
在这里插入图片描述

1.4.4 结果验证

步骤六对实验结果进行了验证，正确检测出异常值。由图可看出，图中的四个圆圈为异常值，分别是 sepal width (cm) 中的第15个，第32个，第33个，第60个数据。

文章来源:https://blog.csdn.net/shaock2018/article/details/135042107
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：veading@qq.com进行投诉反馈，一经查实，立即删除！