Course2-Week3-使用机器学习的建议
Course2-Week3-使用机器学习的建议
- 笔记主要参考B站视频“(强推|双字)2022吴恩达机器学习Deeplearning.ai课程”。
- 该课程在Course上的页面:Machine Learning 专项课程
- 课程资料:“UP主提供资料(Github)”、或者“我的下载(百度网盘)”。
- 本篇笔记对应课程 Course2-Week3(下图中深紫色)。

1. 拆分原始训练集
1.1 如何改进模型
??前面已经介绍了很多“学习算法”,比如线性回归、逻辑回归、深度学习或神经网络,但若算法的性能不好,我们下一步又该做什么来进行改进呢?前面我们只是进行了简单的介绍。比如现在有一个“有正则化的线性回归(Course1-Week3)”,如果训练结束后,发现预测的结果和预期的偏差非常大该怎么办?通常可以考虑以下几个步骤:
- 收集更多的训练样本【耗费大量时间】。
- 减少特征数量。
- 增加特征数量。
- 使用特征的多项式拟合,如 x 1 2 , x 2 2 , x 1 x 2 , e t c x_1^2,x_2^2,x_1x_2,etc x12?,x22?,x1?x2?,etc。
- 减少正则化参数 λ \lambda λ
- 增加正则化参数 λ \lambda λ。
注:2.5节会进一步介绍这些方法的适用场景。
那我们具体要选择哪一个方法呢?如果直接去选择收集更多的样本,最后却发现更多的样本也不能改进算法性能,这显然会浪费大量的时间。所以在机器学习中,做出正确的决策非常重要。
??本周将介绍一系列对机器学习进行“诊断(diagnostic)”的方法,这些方法旨在分析“学习算法”出现异常结果的原因,并据此给出改进性能的指导。“诊断”可能需要时间来实施,但正确的“诊断”显然可以节省大量的时间。本节接下来的两小节,将介绍用于评估算法性能的指标。
1.2 二拆分:训练集、测试集
数学约定:
- m t r a i n m_{train} mtrain?:拆分后,训练集的样本数量。
- m t r a i n m_{train} mtrain?:拆分后,测试集的样本数量。
- ( x ? ( i ) , y ( i ) ) (\vec{x}^{(i)},y^{(i)}) (x(i),y(i)):若没有下标,默认表示是训练集的第 i i i 个样本。
- ( x ? t r a i n ( i ) , y t r a i n ( i ) ) (\vec{x}_{train}^{(i)},y_{train}^{(i)}) (xtrain(i)?,ytrain(i)?):表示是训练集的第 i i i 个样本。
- ( x ? t e s t ( i ) , y t e s t ( i ) ) (\vec{x}_{test}^{(i)},y_{test}^{(i)}) (xtest(i)?,ytest(i)?):表示是测试集的第 i i i 个样本。

- “房价预测问题”贯穿本课程,最早出现在“Course1-Week1的2.2节”。
??我们使用“原始训练集”完成模型的训练后,通常会希望衡量模型的“泛化”能力如何。但是我们手头上除了“原始训练集”也没有其他的样本了。所以,这就启示我们将“原始训练集”进行二拆分(如三七分,或者其他比例),70%作为新的“训练集(train set)”用于正常训练,30%作为“测试集(test set)”用于测试(如上图)。模型训练结束后,通过计算“训练误差(training error)”和“测试误差(test error)”就能衡量模型性能。注意这个“测试误差”和“训练误差”是新定义的,和原本的“损失函数”或“代价函数”毫无关系,有如下三种计算方法:
【场景一】线性回归:将“测试误差”和“训练误差”也定义成“均方误差”的形式。
Linear?cost?function : min ? w ? , b J ( w ? , b ) = 1 2 m t r a i n ∑ i = 1 m t r a i n ( f w ? , b ( x ? ( i ) ) ? y ( i ) ) 2 + λ 2 m t r a i n ∑ j = 1 n w j 2 ? 正则化 Test?error : J t e s t ( w ? , b ) = 1 2 m t e s t ∑ i = 1 m t e s t ( f w ? , b ( x ? t e s t ( i ) ) ? y t e s t ( i ) ) 2 Training?error : J t r a i n ( w ? , b ) = 1 2 m t r a i n ∑ i = 1 m t r a i n ( f w ? , b ( x ? t r a i n ( i ) ) ? y t r a i n ( i ) ) 2 \begin{aligned} \text{Linear cost function} &: \quad \min_{\vec{w},b} J(\vec{w},b) = \frac{1}{2m_{train}} \sum_{i=1}^{m_{train}}(f_{\vec{w},b}(\vec{x}^{(i)})-y^{(i)})^2 + \underbrace{\frac{\lambda}{2m_{train}}\sum_{j=1}^{n}w_j^2}_{\text{正则化}}\\ \text{Test error} &: \quad J_{test}(\vec{w},b) = \frac{1}{2m_{test}} \sum_{i=1}^{m_{test}}(f_{\vec{w},b}(\vec{x}_{test}^{(i)})-y_{test}^{(i)})^2\\ \text{Training error} &: \quad J_{train}(\vec{w},b) = \frac{1}{2m_{train}} \sum_{i=1}^{m_{train}}(f_{\vec{w},b}(\vec{x}_{train}^{(i)})-y_{train}^{(i)})^2\\ \end{aligned} Linear?cost?functionTest?errorTraining?error?:w,bmin?J(w,b)=2mtrain?1?i=1∑mtrain??(fw,b?(x(i))?y(i))2+正则化 2mtrain?λ?j=1∑n?wj2???:Jtest?(w,b)=2mtest?1?i=1∑mtest??(fw,b?(xtest(i)?)?ytest(i)?)2:Jtrain?(w,b)=2mtrain?1?i=1∑mtrain??(fw,b?(xtrain(i)?)?ytrain(i)?)2?【场景二】逻辑回归:将“测试误差”和“训练误差”也定义成“二元交叉熵”的形式。
Logistic?cost?function: min ? w ? , b J ( w ? , b ) = ? 1 m t r a i n ∑ i = 1 m t r a i n [ y ( i ) l o g ( f w ? , b ( x ? ( i ) ) ) + ( 1 ? y ( i ) ) l o g ( 1 ? f w ? , b ( x ? ( i ) ) ) ] + λ 2 m t r a i n ∑ j = 1 n w j 2 ? 正则化 Test?error: J t e s t ( w ? , b ) = ? 1 m t e s t ∑ i = 1 m t e s t [ y t e s t ( i ) l o g ( f w ? , b ( x ? t e s t ( i ) ) ) + ( 1 ? y t e s t ( i ) ) l o g ( 1 ? f w ? , b ( x ? t e s t ( i ) ) ) ] Train?error: J t r a i n ( w ? , b ) = ? 1 m t r a i n ∑ i = 1 m t r a i n [ y t r a i n ( i ) l o g ( f w ? , b ( x ? t r a i n ( i ) ) ) + ( 1 ? y t r a i n ( i ) ) l o g ( 1 ? f w ? , b ( x ? t r a i n ( i ) ) ) ] \begin{aligned} &\begin{aligned} & \text{Logistic cost function:} \\ &\min_{\vec{w},b} J(\vec{w},b) = -\frac{1}{m_{train}} \sum_{i=1}^{m_{train}}[y^{(i)}log(f_{\vec{w},b}(\vec{x}^{(i)}))+(1-y^{(i)})log(1-f_{\vec{w},b}(\vec{x}^{(i)}))] + \underbrace{\frac{\lambda}{2m_{train}}\sum_{j=1}^{n}w_j^2}_{\text{正则化}}\\ \end{aligned}\\ &\begin{aligned} \text{Test error:} & \quad J_{test}(\vec{w},b) = -\frac{1}{m_{test}} \sum_{i=1}^{m_{test}}[y_{test}^{(i)}log(f_{\vec{w},b}(\vec{x}_{test}^{(i)}))+(1-y_{test}^{(i)})log(1-f_{\vec{w},b}(\vec{x}_{test}^{(i)}))]\\ \text{Train error:} & \quad J_{train}(\vec{w},b) = -\frac{1}{m_{train}} \sum_{i=1}^{m_{train}}[y_{train}^{(i)}log(f_{\vec{w},b}(\vec{x}_{train}^{(i)}))+(1-y_{train}^{(i)})log(1-f_{\vec{w},b}(\vec{x}_{train}^{(i)}))]\\ \end{aligned} \end{aligned} ??Logistic?cost?function:w,bmin?J(w,b)=?mtrain?1?i=1∑mtrain??[y(i)log(fw,b?(x(i)))+(1?y(i))log(1?fw,b?(x(i)))]+正则化 2mtrain?λ?j=1∑n?wj2????Test?error:Train?error:?Jtest?(w,b)=?mtest?1?i=1∑mtest??[ytest(i)?log(fw,b?(xtest(i)?))+(1?ytest(i)?)log(1?fw,b?(xtest(i)?))]Jtrain?(w,b)=?mtrain?1?i=1∑mtrain??[ytrain(i)?log(fw,b?(xtrain(i)?))+(1?ytrain(i)?)log(1?fw,b?(xtrain(i)?))]??【场景3】逻辑回归:对于分类问题,也可以直接计算更简洁的“错误样本占比”(需要选定二元分类的阈值)。
Logistic?cost?function: min ? w ? , b J ( w ? , b ) = ? 1 m t r a i n ∑ i = 1 m t r a i n [ y ( i ) l o g ( f w ? , b ( x ? ( i ) ) ) + ( 1 ? y ( i ) ) l o g ( 1 ? f w ? , b ( x ? ( i ) ) ) ] + λ 2 m t r a i n ∑ j = 1 n w j 2 ? 正则化 Test?error: 测试集中,预测错误的样本占比 Train?error: 训练集中,预测错误的样本占比 \begin{aligned} &\begin{aligned} & \text{Logistic cost function:} \\ &\min_{\vec{w},b} J(\vec{w},b) = -\frac{1}{m_{train}} \sum_{i=1}^{m_{train}}[y^{(i)}log(f_{\vec{w},b}(\vec{x}^{(i)}))+(1-y^{(i)})log(1-f_{\vec{w},b}(\vec{x}^{(i)}))] + \underbrace{\frac{\lambda}{2m_{train}}\sum_{j=1}^{n}w_j^2}_{\text{正则化}}\\ \end{aligned}\\ &\begin{aligned} \text{Test error:} & \quad \text{测试集中,预测错误的样本占比}\\ \text{Train error:} & \quad \text{训练集中,预测错误的样本占比}\\ \end{aligned} \end{aligned} ??Logistic?cost?function:w,bmin?J(w,b)=?mtrain?1?i=1∑mtrain??[y(i)log(fw,b?(x(i)))+(1?y(i))log(1?fw,b?(x(i)))]+正则化 2mtrain?λ?j=1∑n?wj2????Test?error:Train?error:?测试集中,预测错误的样本占比训练集中,预测错误的样本占比??
于是,“测试误差 J t e s t J_{test} Jtest?”便可以用来评估模型的泛化程度。下面是如何使用“测试误差 J t e s t J_{test} Jtest?”和“训练误差 J t r a i n J_{train} Jtrain?”进行判断:
- 过拟合: J t r a i n J_{train} Jtrain? 很小,甚至为0;而 J t e s t J_{test} Jtest? 则很大。
- 欠拟合: J t r a i n J_{train} Jtrain? 和 J t e s t J_{test} Jtest? 都很大。
注1:这里的“很小”、“很大”只是一种抽象的比较,2.3节将介绍具体的衡量基准。
注2:这里的判断还不完善,具体见下一节。
1.3 三拆分:训练集、验证集、测试集
数学约定:
- m c v m_{cv} mcv?:拆分后,交叉验证集的样本数量。
- ( x ? c v ( i ) , y c v ( i ) ) (\vec{x}_{cv}^{(i)},y_{cv}^{(i)}) (xcv(i)?,ycv(i)?):表示是交叉验证集的第 i i i 个样本。
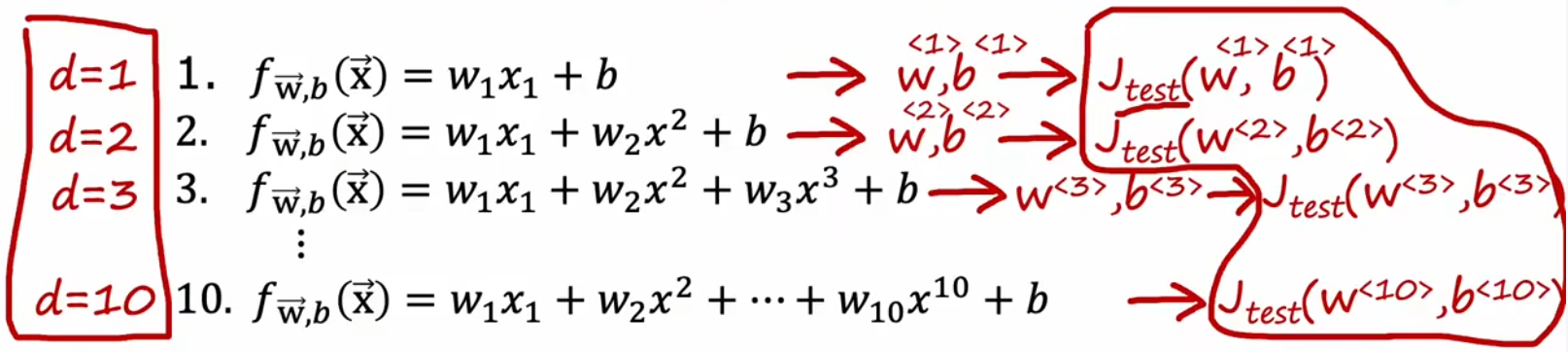
??虽然上一小节介绍的“二拆分”看起来很不错,但是也有局限性。比如“房价预测问题”中存在许多可能的多项式模型(使用 d d d 表示不同的最高幂次),我们要选择最合适的,显然可以选择 J t e s t J_{test} Jtest? 最小的模型。但一旦这么做,就会导致“训练集”也用于模型的训练(优化参数 d d d),这就导致 J t e s t J_{test} Jtest? 可能要比实际上的泛化误差低。于是来进行改进,将模型进行“三拆分”(比如下面的622,其他比例也可以):
- “训练集(train set)”(60%):用于训练模型。计算出的“训练误差 J t r a i n J_{train} Jtrain?”用于衡量训练的效果。
- “交叉验证集(cross validation set)”(20%):用于计算“验证误差 J c v J_{cv} Jcv?”,并利用其选择合适的模型整体参数,比如“房价预测问题”中的多项式次数、神经网络的层数/神经元数量、模型的正则化参数(2.2节)等。
- 这个名字有点绕口,但这是机器学习领域的人们命名的,或者也简称为“验证集(validation set)”、“开发集(development set / dev set)”。老师最常使用“dev set”,本文默认使用“验证集”。
- “测试集(test set)”(20%):用于计算“测试误差 J t e s t J_{test} Jtest?”,来衡量“泛化误差(generalization error)”。
【场景一】线性回归:将“测试误差”、“验证误差”、“训练误差”都定义成“均方误差”的形式。
Training?error : J t r a i n ( w ? , b ) = 1 2 m t r a i n ∑ i = 1 m t r a i n ( f w ? , b ( x ? t r a i n ( i ) ) ? y t r a i n ( i ) ) 2 Cross?validation?error /?Validation?error?/?Dev?error : J c v ( w ? , b ) = 1 2 m c v ∑ i = 1 m c v ( f w ? , b ( x ? c v ( i ) ) ? y c v ( i ) ) 2 Test?error : J t e s t ( w ? , b ) = 1 2 m t e s t ∑ i = 1 m t e s t ( f w ? , b ( x ? t e s t ( i ) ) ? y t e s t ( i ) ) 2 \begin{aligned} \text{Training error} &: \quad J_{train}(\vec{w},b) = \frac{1}{2m_{train}} \sum_{i=1}^{m_{train}}(f_{\vec{w},b}(\vec{x}_{train}^{(i)})-y_{train}^{(i)})^2 \\ \begin{aligned} \text{Cross validation error}\\ \text{/ Validation error / Dev error}\\ \end{aligned} &: \quad J_{cv}(\vec{w},b) = \frac{1}{2m_{cv}} \sum_{i=1}^{m_{cv}}(f_{\vec{w},b}(\vec{x}_{cv}^{(i)})-y_{cv}^{(i)})^2\\ \text{Test error} &: \quad J_{test}(\vec{w},b) = \frac{1}{2m_{test}} \sum_{i=1}^{m_{test}}(f_{\vec{w},b}(\vec{x}_{test}^{(i)})-y_{test}^{(i)})^2\\ \end{aligned} Training?errorCross?validation?error/?Validation?error?/?Dev?error?Test?error?:Jtrain?(w,b)=2mtrain?1?i=1∑mtrain??(fw,b?(xtrain(i)?)?ytrain(i)?)2:Jcv?(w,b)=2mcv?1?i=1∑mcv??(fw,b?(xcv(i)?)?ycv(i)?)2:Jtest?(w,b)=2mtest?1?i=1∑mtest??(fw,b?(xtest(i)?)?ytest(i)?)2?注1:上面的计算公式只是“均方误差”的形式,当然可以和“1.2节”相同,也有“二元交叉熵”、“错误样本占比”等形式。
注2:模型预测效果异常时,“训练误差”和“验证误差”还可以用于判断模型的异常原因(2.1节)。
注3:若无需优化模型的整体参数,只需训练集和测试集,那也可以只进行二拆分(如3.4节-迁移学习)。但前期开发都需要三拆分。

??回到“房价预测问题”,现在我们进行三拆分之后,就可以使用“训练集”训练模型,然后使用“验证集”取计算每个模型的误差,并找出“验证误差”最小的参数,假设是 J c v ( w < 4 > , b < 4 > ) J_{cv}(w^{<4>},b^{<4>}) Jcv?(w<4>,b<4>),最后就可以使用“测试集”来计算当前模型的泛化误差了。由于没有使用“测试集”拟合任何参数,所以此时“测试集”就能良好的反映出模型的“泛化误差”。
同样的,我们也可以使用“验证误差”来决定神经网络的层数和每层的神经元数量。如下图,“验证误差” J c v ( w < 2 > , b < 2 > ) J_{cv}(w^{<2>},b^{<2>}) Jcv?(w<2>,b<2>) 最小,于是第二个结构的神经网络就是最合适的:

最后注意的是,三拆分后,要使用“训练误差 J t r a i n J_{train} Jtrain?”、“验证误差 J c v J_{cv} Jcv?”对模型进行判断 【重点】:
- 过拟合: J t r a i n J_{train} Jtrain? 很小,甚至为0;而 J c v J_{cv} Jcv? 则很大。
- 欠拟合: J t r a i n J_{train} Jtrain? 和 J c v J_{cv} Jcv? 都很大。
- 恰当: J t r a i n J_{train} Jtrain? 和 J c v J_{cv} Jcv? 都很小。
注1:这里的“很小”、“很大”只是一种抽象的比较,2.3节将介绍具体的衡量基准。
注2:“测试误差 J t e s t J_{test} Jtest?”只用于评估模型的泛化程度。
本节 Quiz:
In the context of machine learning, what is a diagnostic?
× This refers to the process of measuring how well a learning algorithm does on a test set (data that the algorithm was not trained on).
√ A test that you run to gain insight into what is/isn’t working with a learning algorithm, to gain guidance into improving its performance.
× An application of machine learning to medical applications, with the goal of diagnosing patients’ conditions.
× A process by which we quickly try as many different ways to improve an algorithm as possible, so as to see what works.It is always true that the better an algorithm does on the training set, the better it will do on generalizing to new data.
√ False
× TrueFor a classification task; suppose you train three different models using three different neural network architectures. Which data do you use to evaluate the three models in order to choose the best one?
× The test set.
× All the data - training, cross validation and test sets put together.
√ The cross validation set.
× The training set.注:此题是开发前期在选择模型,用于后续继续迭代开发。而不是有三个成熟方案,直接找一个测试误差最小的。
2. 避免高偏差和高方差
??本节学习如何分析模型的“偏差(bias)”和“方差(variance)”,并介绍一系列避免“高偏差”或“高方差”的方法。注意,“偏差”和“方差”是非常重要的概念,是对模型进行“诊断”的最重要的工具之一,老师提到自己一个工作多年的博士说过:
- 虽然“偏差”和“方差”很容易就学会了,但是需要一辈子才能真正掌握。
2.1 使用训练误差和验证误差进行分析

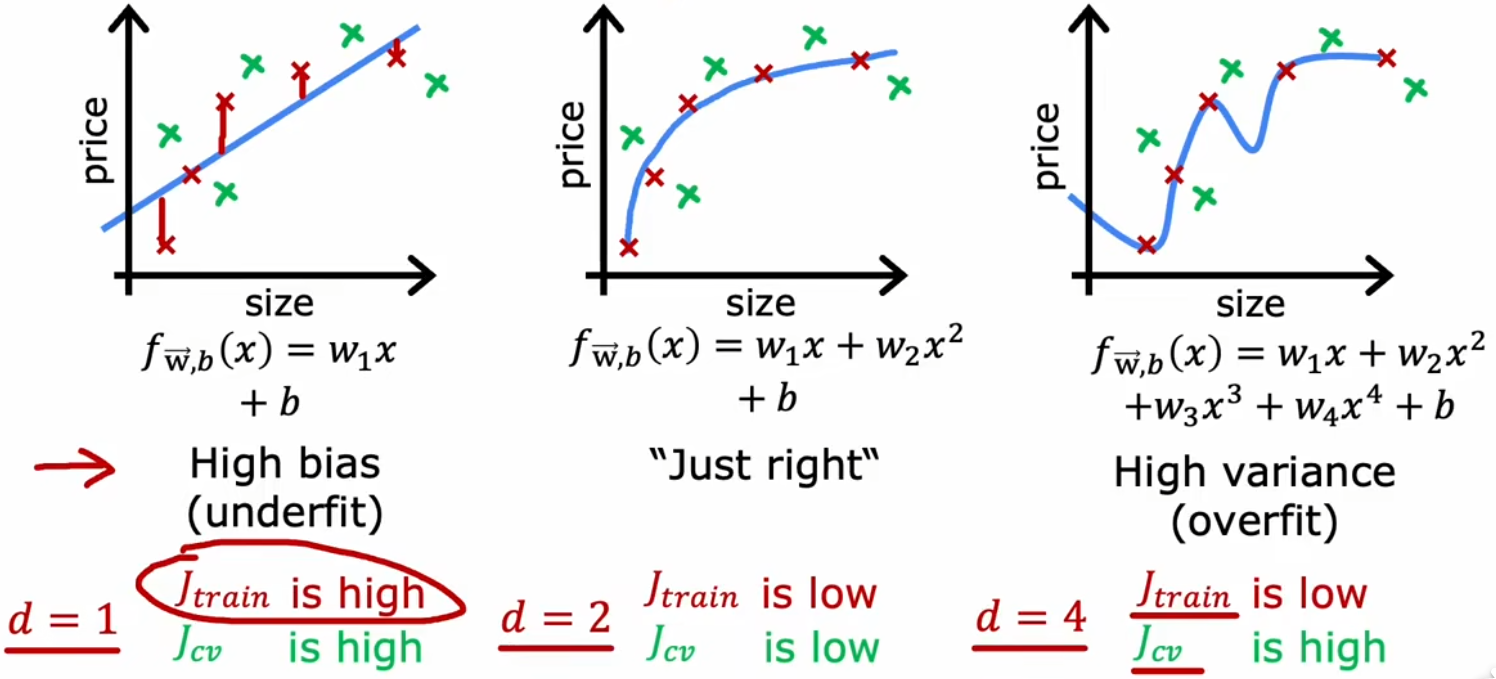
??前面几周提到,“高偏差”等价于“欠拟合”、“高方差”等价于“过拟合”,所以“偏差(bias)”和“方差(variance)”是“诊断”模型非常重要的概念。上一大节的最后,已经介绍了如何使用“训练误差”和“验证误差”来判断模型的拟合情况(如上图)。现在不妨继续以“房价预测问题”为例,观察“训练误差”和“验证误差”是如何随着模型最高幂次 d d d 变化的:
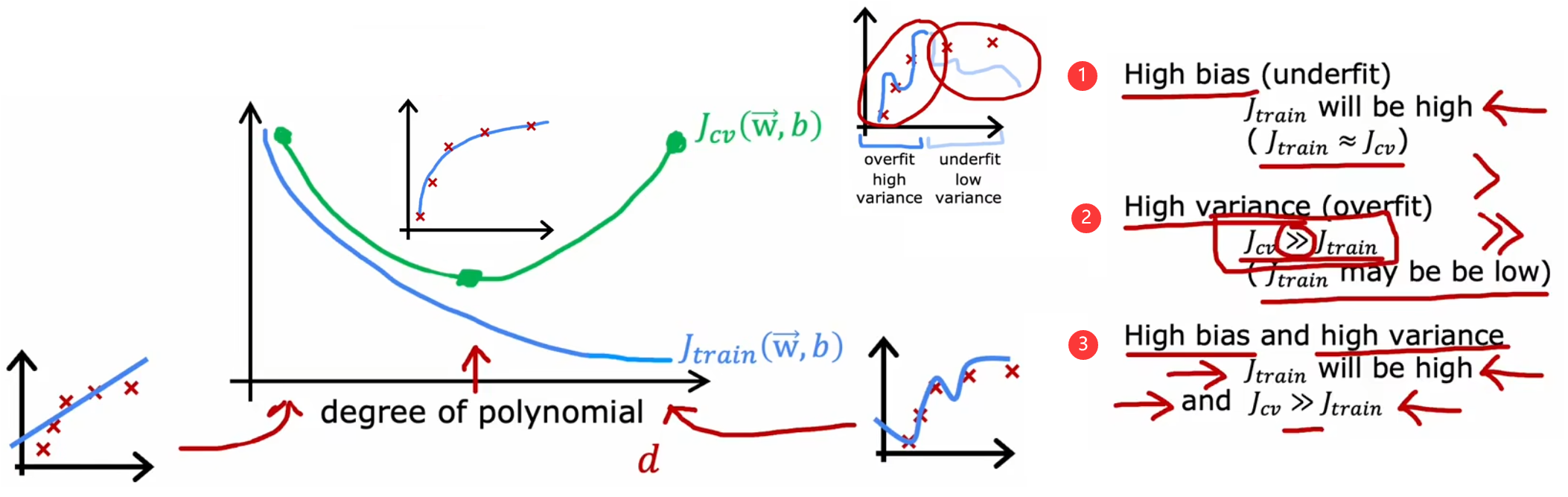
- 高偏差(欠拟合): d d d 较小时, J t r a i n J_{train} Jtrain?、 J c v J_{cv} Jcv? 都很大。
- 恰当: d d d 恰当时, J t r a i n J_{train} Jtrain?、 J c v J_{cv} Jcv? 都相对较小。
- 高方差(过拟合): d d d 较大时, J t r a i n J_{train} Jtrain? 较小、且 J c v J_{cv} Jcv? 远大于 J t r a i n J_{train} Jtrain?。
- 高偏差且高方差: J t r a i n J_{train} Jtrain? 较大、且 J c v J_{cv} Jcv? 更是远大于 J t r a i n J_{train} Jtrain?。某些神经网络模型可能会出现这种情况。
总结: J t r a i n J_{train} Jtrain? 用于看是否“高偏差”, J c v J_{cv} Jcv? 和 J t r a i n J_{train} Jtrain? 的差值用于看是否“高方差”。
??当模型的预测不理想时,只有首先判断模型是“高偏差”还是“高方差”,才能对症下药,解决模型中的问题。下面几个小节就来依次介绍这些解决方法。
2.2 选择合适的正则化参数

- λ \lambda λ过大:强烈抑制所有模型参数,导致模型过于简化,于是“高偏差”。
- λ \lambda λ适中:情况较为理想,可以恰当的只抑制某些高阶特征的参数。
- λ \lambda λ过小:相当于没有正则化,很可能“高方差”。
??“Course1-Week3的4.3节-正则化”已经介绍过“正则化”,可以帮助我们避免“高方差”,但是正则化参数 λ \lambda λ 过大又可能会导致“高偏差”(如上图)。之前我们只是简单的说了一句 “ λ \lambda λ 不要太大”,本节来具体介绍如何选择最合适的 λ \lambda λ。
回到“房价预测问题”,假定现在已经确定了模型为四阶多项式,所以可以使用“验证集”选择合适的正则化参数 λ \lambda λ。和“1.3节”使用“验证集”选择最合适的模型幂次相似,设置不同的 λ \lambda λ 作为待选择的模型参数,然后分别计算这个参数所对应的“验证误差”,最小的“验证误差”所对应的 λ \lambda λ 即为最优,如下图最小的 J c v ( w < 5 > , b < 5 > ) J_{cv}(w^{<5>},b^{<5>}) Jcv?(w<5>,b<5>) 对应参数为 λ = 0.08 \lambda=0.08 λ=0.08。下图还给出“训练误差”、“验证误差”随着 λ \lambda λ 变化的曲线:

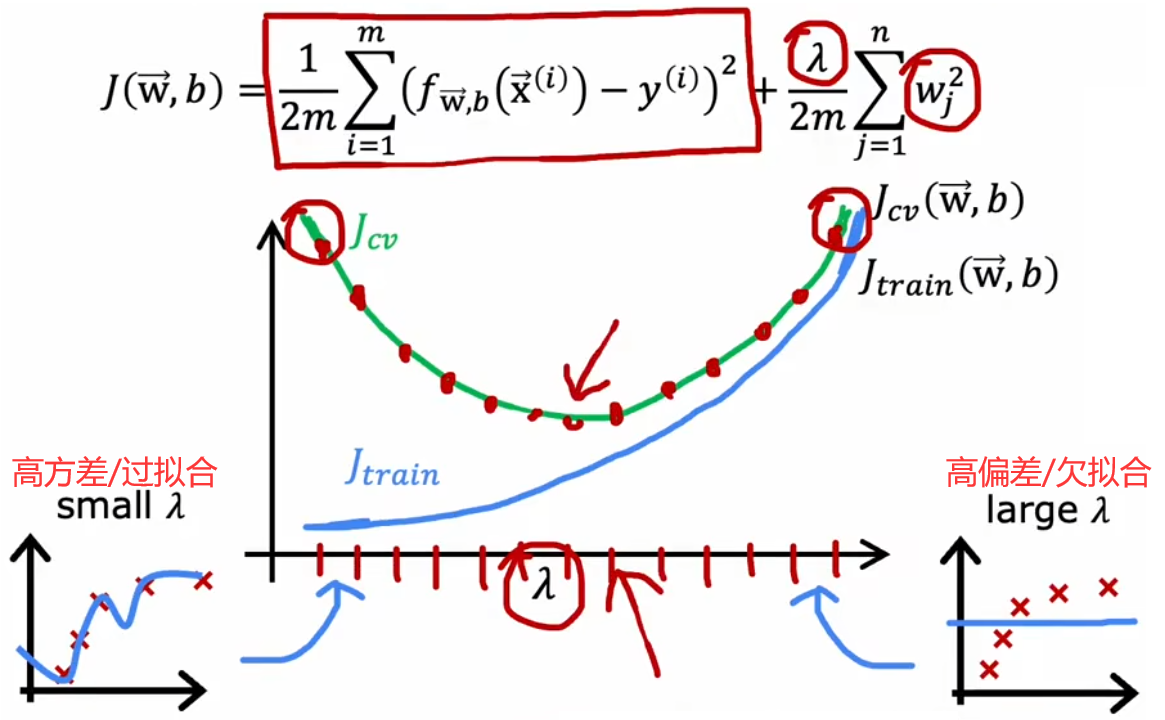
- λ \lambda λ过小: J t r a i n J_{train} Jtrain? 较小、且 J c v J_{cv} Jcv? 远大于 J t r a i n J_{train} Jtrain?,此时“高方差”。
- λ \lambda λ适中: J t r a i n J_{train} Jtrain?、 J c v J_{cv} Jcv? 都相对较小,模型合适。
- λ \lambda λ过大: J t r a i n J_{train} Jtrain?、 J c v J_{cv} Jcv? 都很大,此时“高偏差”。
注意到本曲线和上一小节的曲线类似于“镜像关系”,这是因为欠拟合和过拟合的位置,在两张图中互为镜像。
下一节将具体衡量 J c v J_{cv} Jcv? 和 J t r a i n J_{train} Jtrain? 的大小,而不是像现在只是一个模糊的比较。
2.3 性能评估的基准
??前面介绍了如何使用 J c v J_{cv} Jcv? 和 J t r a i n J_{train} Jtrain? 判断“高偏差”/“高方差”,但是一直是很模糊的“很大”、“很小”,本节就来介绍如何具体衡量 J c v J_{cv} Jcv? 和 J t r a i n J_{train} Jtrain? 的大小。想要衡量一个指标的具体大小时,通常需要一个“基准”。构建“基准”的常见方法是:
- 使用人类在解决该问题时的误差。因为人类很擅长理解语音处理、图像、文本等,使用上述非结构化数据时,人类就是很好的基准。
- 使用之前存在的算法的误差。也就是,之前有人提出过算法解决当前问题,所以可以把以前的算法作为基准。
注(ChatGPT):“非结构化数据”这个术语通常用来描述那些不容易通过传统的表格或数据库形式表示的数据。
??比如下面的“语音识别应用”中,某算法的“训练误差”为 J t r a i n = 10.8 % J_{train}=10.8\% Jtrain?=10.8%,那么能说这个算法的训练效果很差吗?并不能。因为人类对这些音频进行转录时,转换错误的样本占比为 10.6 % 10.6\% 10.6%, J t r a i n J_{train} Jtrain? 和人类的“错误占比”持平。所以在没找到“基准”之前,不要盲目说“训练误差”很大:
“语音识别应用”:将语音转换成文本。
- 输入:一段音频。比如“今天天气怎么样”、“最近的咖啡店在哪里”等。
- 输出:转换后的文字。“错误”被定义为转换失败的样本占比。

- 第一列数据: J t r a i n J_{train} Jtrain? 和“基准”持平,所以“偏差”不高; J c v J_{cv} Jcv? 远高于 J t r a i n J_{train} Jtrain?,所以“高方差”。
- 第二列数据: J t r a i n J_{train} Jtrain? 远高于“基准”,所以“高偏差”; J c v J_{cv} Jcv? 和 J t r a i n J_{train} Jtrain? 持平,所以“方差”不高。
- 第三列数据: J t r a i n J_{train} Jtrain? 远高于“基准”,所以“高偏差”; J c v J_{cv} Jcv? 远高于 J t r a i n J_{train} Jtrain?,所以“高方差”。两者兼有。
2.4 训练集的样本数量
??本节来讨论一下,一味的“增加训练样本数量”能否不断地改善模型性能。先说结论,到达一定限度后,增加训练样本数量并不能改善模型性能。现在回到“房价预测问题”,使用“最合适的二阶多项式模型”、“高偏差模型”、“高方差模型”,下面画出其学习曲线,横坐标是“训练集大小”,纵坐标是 J c v J_{cv} Jcv? 和 J t r a i n J_{train} Jtrain? 的大小:

- J c v J_{cv} Jcv?:随着训练样本的增多,模型的泛化能力越强, J c v J_{cv} Jcv? 下降表明方差减小,符合直观。
- J t r a i n J_{train} Jtrain?:训练集越大,越难完美拟合全部训练样本,所以 J t r a i n J_{train} Jtrain? 会逐渐增大,但是模型的泛化能力会增强。
- J c v J_{cv} Jcv? 通常会高于 J t r a i n J_{train} Jtrain?。
注:“学习曲线”的种类很多,上述只是其中之一。
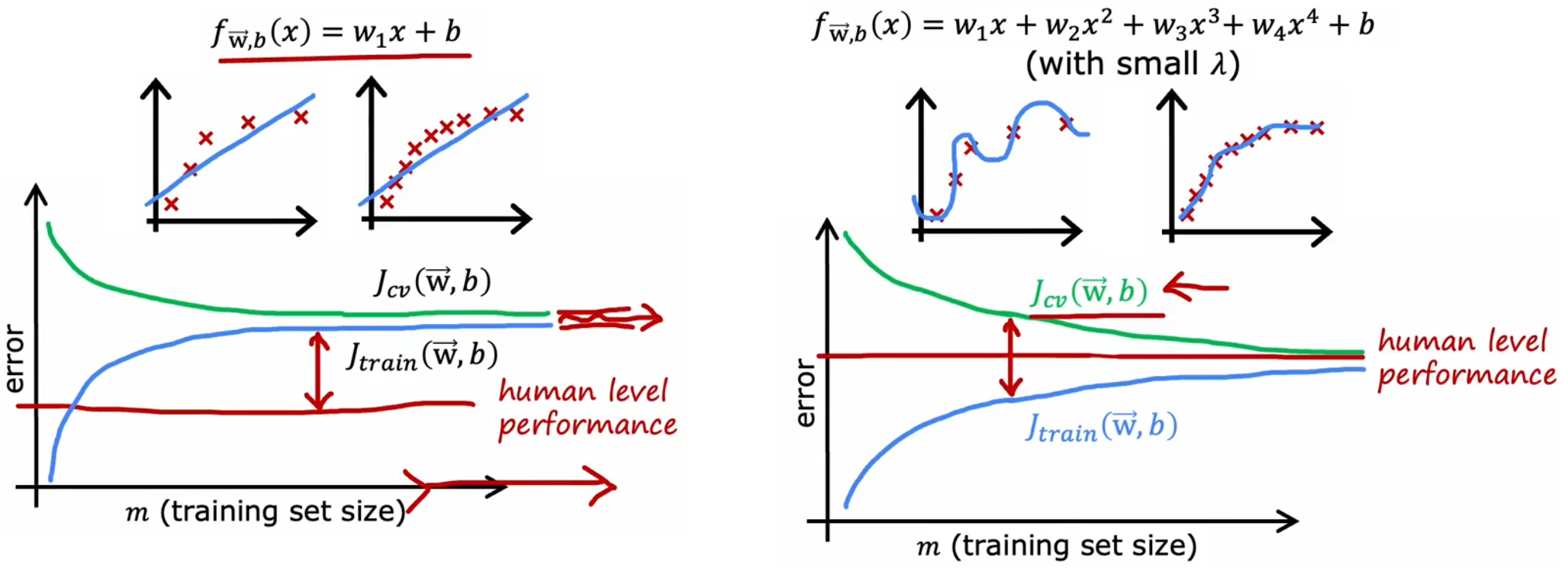
- 高偏差(上左图): J t r a i n J_{train} Jtrain? 远高于“基准线”。更过的训练样本并不会降低 J t r a i n J_{train} Jtrain?、 J c v J_{cv} Jcv?,所以应该改进模型。
- 高方差(上右图):增加样本会提升模型的性能,但这通常会需要远超一个合适的模型所需的样本。但当然,样本获取较为简单时,力大砖飞也不是不行。
通过上面三个图片可以看到,对于“合适的模型”来说,增加样本才能显著提升系统性能。而如果模型本身不合适时,首先考虑的应当是改进模型,而不是一味的增加训练数据。所以实际上,在进行正式的训练之前,可以先画出上述曲线判断一下模型是否存在“高偏差”或“高方差”。但显然,这种方法的缺点就是计算量会非常大,所以实际上不会完整地画出上述曲线,但是记住上述学习曲线的样子,有助于判断模型潜在的问题。
2.5 如何改进模型(修订)
??于是现在可以回到本周最初的“房价预测”问题。在使用 J t r a i n J_{train} Jtrain? 和 J c v J_{cv} Jcv? 判断“高偏差”、“高方差”之后,下面的方法都是对症下药:
- 【解决高方差】收集更多的训练样本。
- 【解决高方差】减少特征数量。
- 【解决高偏差】增加特征数量。
- 【解决高偏差】使用特征的多项式拟合,如 x 1 2 , x 2 2 , x 1 x 2 , e t c x_1^2,x_2^2,x_1x_2,etc x12?,x22?,x1?x2?,etc。
- 【解决高偏差】减少正则化参数 λ \lambda λ
- 【解决高方差】增加正则化参数 λ \lambda λ。
总结:解决高方差,就收集样本或简化模型;解决高偏差,就使模型更复杂、灵活。
注:不管怎样,都不要通过“减少训练样本”这样取巧作弊的方式来解决问题。
2.6 神经网络的偏差与方差
??虽然上述一直用“房价预测”这样简单的回归问题来举例子,但对于神经网络来说,分析方法都是一样的,并且神经网络还有一些特殊的优点。在神经网络出现之前,工程师通常会在“高偏差”和“高方差”之间做出权衡(如同前面所讲)。但由于神经网络通常会有一个很大的训练集,再加上大型神经网络是一个“低偏差”系统。也就是说,只要神经网络足够大,总是可以达到很小的“偏差”,大型神经网络可以拟合非常复杂的函数。于是,对于神经网络的训练来说,通常采用“力大砖飞”法:
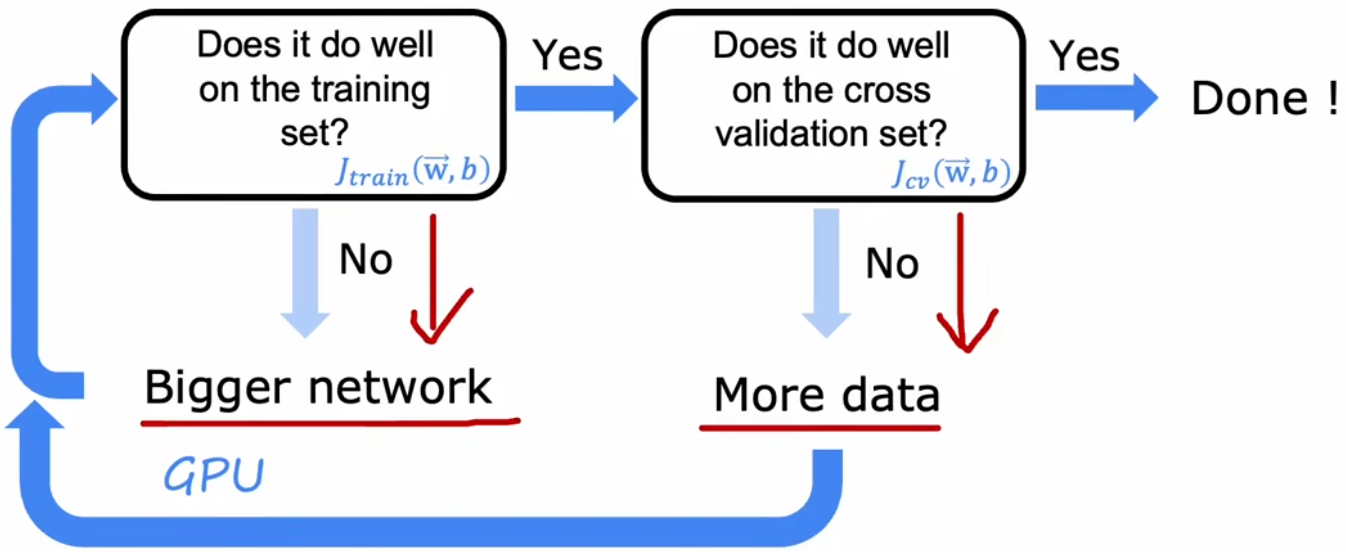
- 判断训练误差:若 J t r a i n J_{train} Jtrain? 较小,进行下一步;若 J t r a i n J_{train} Jtrain? 较大,则扩大神经网络结构。
- 判断验证误差:若 J c v J_{cv} Jcv? 较小,训练完成!若 J c v J_{cv} Jcv? 较大,收集更多的数据回到前一步重新训练。
缺点:
- 训练成本昂贵。训练更大的神经网络确实可以减小偏差,但也意味着计算成本更高。
- 数据集很难获取。好的数据集总是很难获取。不过现在是大数据时代,数据集的获取比以前会更简单。
上述说到大型神经网络是低偏差系统,所以训练神经网络时,通常只会关心“高方差/过拟合”的问题。实际上,虽然大型神经网络看似“模型更复杂”,但也不会导致“过拟合”。实际上,只要有恰当的正则化,大型神经网络通常会和小型网络的性能一样好甚至更好,只不过会提高计算成本。所以为了防止神经网络过拟合,通常会收集更多数据【下策】、调整正则化参数【上策】。下面是神经网络正则化的公式和代码示例:
Neural?Network?Cost?Funtion:
J
(
W
,
B
)
=
1
m
∑
i
=
1
m
L
(
f
(
x
?
(
i
)
)
,
y
(
i
)
)
+
λ
2
m
∑
w
2
?
all?weights
??
w
\text{Neural Network Cost Funtion:} \quad J(\bold{W},\bold{B}) = \frac{1}{m}\sum_{i=1}^m L(f(\vec{x}^{(i)}),y^{(i)}) + \frac{\lambda}{2m} \underbrace{\sum w^2}_{\text{all weights}\; \bold{w}}
Neural?Network?Cost?Funtion:J(W,B)=m1?i=1∑m?L(f(x(i)),y(i))+2mλ?all?weightsw
∑w2??
# 没有正则化的神经网络
model = Sequential([Dense(units=25, activation="relu"),
Dense(units=15, activation="relu"),
Dense(units=1, activation="sigmoid")])
# 有正则化的神经网络
model = Sequential([Dense(units=25, activation="relu", kernel_regularizer=L2(0.01)),
Dense(units=15, activation="relu", kernel_regularizer=L2(0.01)),
Dense(units=1, activation="sigmoid", kernel_regularizer=L2(0.01))])
####################################################
# 关于正则化L1和L2:
# L1:参数的绝对值的均值,对于所有参数一视同仁的增加或减小。
# L2:参数的平方的均值,对于高次幂的参数更加敏感,更常用。
####################################################
本节 Quiz:
If the model’s cross validation error J c v J_{cv} Jcv? is much higher than the training error J t r a i n J_{train} Jtrain?, this is an indication that the model has…
√ high variance
× high bias
× Low variance
× Low biasWhich of these is the best way to determine whether your model has high bias (has underfit the training data)?
× See if the training error is high (above 15% or so).
× Compare the training error to the cross validation error.
√ Compare the training error to the baseline level of performance.
× See if the cross validation error is high compared to the baseline level of performance.启示:判断一个指标是不是很高,一定要找一个“基准”,不要想当然。
You find that your algorithm has high bias. Which of these seem like good options for improving the algorithm’s performance? Hint: two of these are correct.
× Collect more training examples.
√ Decrease the regularization parameter λ \lambda λ.
× Remove examples from the training set.
√ Collect additional features or add polynomial features.You find that your algorithm has a training error of 2%, and a cross validation error of 20% (much higher than the training error). Based on the conclusion you would draw about whether the algorithm has a high bias or high variance problem, which of these seem like good options for improving the algorithm’s performance? Hint: two of these are correct.
√ Collect more training data.
√ Increase the regularization parameter λ \lambda λ.
× Decrease the regularization parameter λ \lambda λ.
× Reduce the training set size.
3. 机器学习项目开发的技巧
本节介绍机器学习项目开发的完整周期,并介绍这些过程中可以用到的小技巧。
这几节可能很松散,但这是由于不同的任务场景中,机器学习面临的问题不同。
3.1 前期开发过程的迭代
??首先来看看机器学习在前期开发过程中,如何进行迭代训练:
- 选择模型:决定系统的整体架构,并选择系统中需要使用哪些参数。
- 训练模型:第一次训练时,通常都不会成功。
- 诊断分析:分析错误原因,比如查看“偏差”和“方差”、进行“误差分析”(下一节)。然后重新改进模型。
不断重复上述迭代过程,直到性能达到预期要求。

??假设现在使用“垃圾邮件分类器”举例(如下),在完成最初的训练后,结果并不如预期,可能会想到改进方法如下:
【问题1】“垃圾邮件分类器”:识别垃圾邮件,属于文本分类问题。
- 输入特征:列出英文中最常见的10000个单词,然后统计邮件中是否出现相应的单词。
- 输出:是否为垃圾邮件1/0?
可能的改进方法:
- 收集更多的垃圾邮件训练集。比如“蜜罐计划”故意创造大量假地址,收集垃圾邮件。
- 依据邮件的路由信息定义更复杂的特征。比如邮件头通常包括路由信息。
- 依据邮件内容改进特征。比如将“discounting”和“discount”视作相同的单词。
- 设计识别错别字的算法。比如识别出“w4tchs”、“Med1cine”、“M0rgages”等,这种垃圾邮件最显著的特征。
那我们该如何从这些方法中,选出最有效的方法呢?下一节介绍。
3.2 误差分析
??“误差分析”是除了“偏差和方差”以外,另一组诊断方法。“误差分析”指的是将“验证集”中分类错误的样本进行手动分组,观察这些错误样本是否有相似的主题或特征。回到“垃圾邮件分类器”中,假设现在“验证集”有500个样本,但是有100个错误的分类。我们手动分类这些出现错误的样本,并发现可以分为以下几类(蓝色的数字表示数量):

显然,应该首先解决“药品”或“盗窃密码”主题的问题,比如收集更多“药品”或“盗窃密码”主题的数据集,或者改进输入特征等。而解决“错别字”问题并不能显著提升系统性能!也就不值得花太多时间去修复。对应上一节的方法二、四并不值得首先考虑,方法一有些困难,方法三值得一试。
??最后要说,误差分析更容易解决人类擅长的问题,但对于人类也不擅长的任务,误差分析就会很困那,比如分析“人们会在网页上点击哪个广告”这种相当随机的问题。但总的来说,“误差分析”是一个很有用的工具,并可能帮助避免大量的徒劳工作。
注1:如果“验证集”错误样本数量过多,无法全部手动分组,那也可以随机抽取出某一小部分子集进行分析。
3.3 增加数据集的方法
??一个好的数据集可以让神经网络的训练事半功倍。若“误差分析”的分类结果说明目前的算法对于某一类数据的表现很差,那么额外收集一点此类型的数据集,就可以获得很大的性能提升。而不是再继续收集所有类型的数据集,不仅耗时耗力,并且性能也不会提升很多。比如上一节对于“药品”分类效果很差,就可以只专注于收集“药品主题”的邮件,从而获得更多的性能提升。那该如何获取更多特定类型的数据呢?除了实际收集,还有下面两种高效的创造数据集的方法:
方法一:数据增强
??“数据增强(data augmentation)”使用现有数据集创建全新的数据集。对输入X应用变换或失真,来创建另一个具有相同标签的示例。该技术常用于图像或音频领域,用于增加数据集大小:

- 图像的数据增强:常见的可以旋转、缩放、改变对比度、镜像、扭曲 。
- 语音的数据增强:添加不同的背景噪音、人工制造电话失真等。
注意上述“数据增强”应该是“测试集”中典型的失真类型,不能乱加无意义的失真,比如对“A”图像中的每个像素点都加入噪声,这并没有改变“A”的形状,所以并不能看成是一个新的训练集。
方法二:合成数据
??“合成数据(synthetic data)”是从头开始构建全新的数据,而不是修改原有的训练数据。相比于“数据增强”来说,“合成数据”的应用领域较少,通常只用于计算机视觉。比如下面的“字符识别”中,左侧是现实世界中拍照的字体;右侧是对理想字体人为编码添加一些失真,两者相似,可以认为是同类型的数据集。虽然编写代码添加失真的过程需要一些时间,但是一旦设置好后就会获得大量的数据集,进而为神经网络性能带来巨大的提升:

- 原始数据:从现实世界拍摄的照片。
- 合成数据:对不同的标准字体进行人工添加失真,再进行截图得到的数据。
总结:数据的重要性
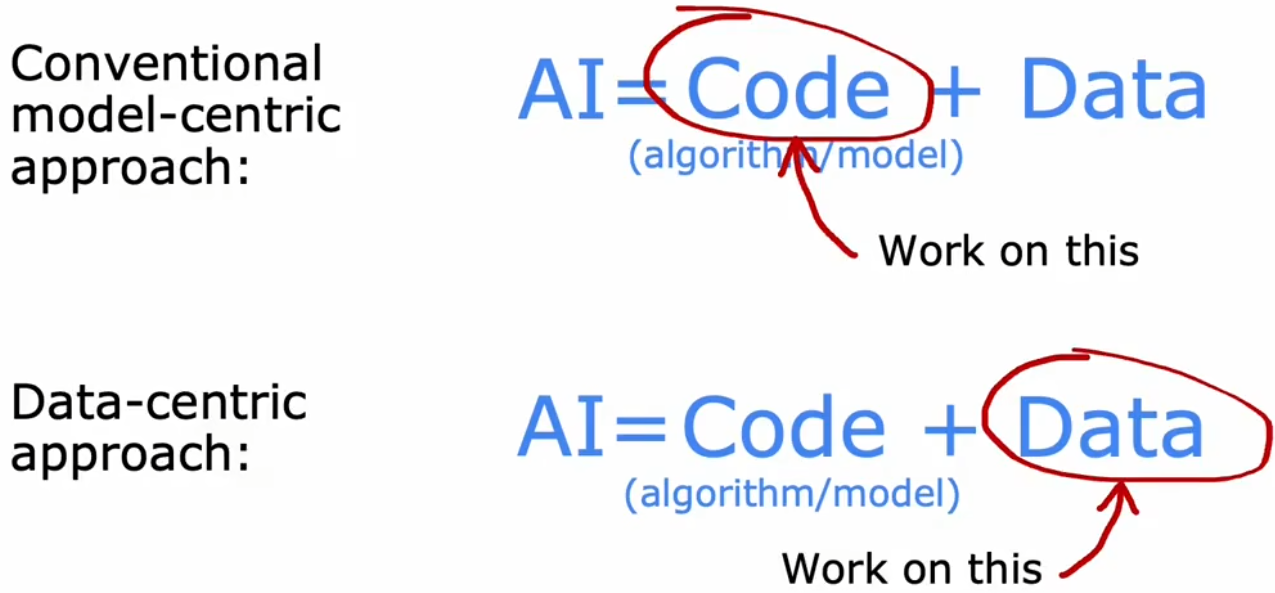
??几十年前,研究人员更专注于研究更先进的机器学习算法。而现在,得益于机器学习的固定范式,很多算法已经足够好,可以解决很多任务,所以目前的研究重点转到“数据集”上来。一个好的数据集可能会带来更多的性能提升。
但有些问题没有那么多的数据集,并且很难获取,又该怎么办呢?下一节“迁移学习”可以借鉴其他相似任务的模型,进而使用较少的数据集完成训练。并不总是有用,但若是有用可以有很大帮助。
3.4 迁移学习-借鉴他人的模型
【问题1】“图片分类”:
- 输入特征:200x200的图片。训练集大小为10万。
- 输出:猫、狗、车等共1000个分类。
【问题2】“手写数字识别”:
- 输入特征:200x200的手写数字图片。训练集大小只有50。
- 输出:0~9共10个分类。
??若想解决一些没有太多数据集的问题,那么可以首先考虑“迁移学习(transfer learning)”,也就是借鉴别人的智慧。比如针对上述的“【问题1】图片分类”,下图中已经有一个训练好的神经网络。此时,我们想进行“手写数字识别”,但数据集只有50张图片非常小,重新训练一个新的神经网络显然不可能。于是我们就可以进行“迁移学习”,将前面训练好的大型神经网络拷贝下来,保留所有隐藏层不动,只替换其输出层,然后重新训练即可:
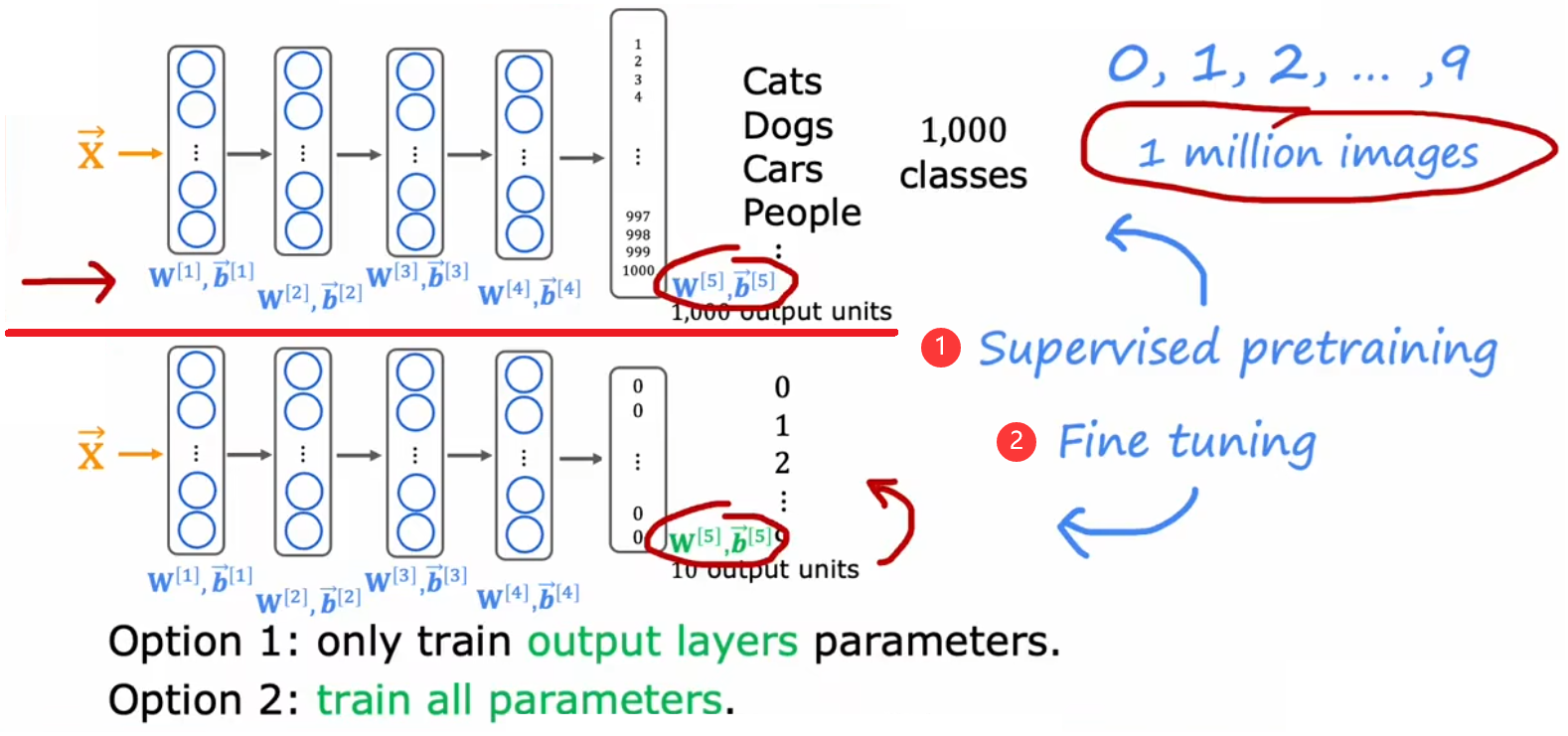
即使我们的数据集非常小,最后也可以获得相当不错的训练效果。这也是因为两项任务要求相似,所以才能进行借鉴。下面给出“迁移学习”的一般步骤及其注意事项:
- 有监督的预训练(supervised pre-training):首先对有较大的数据集的其他相似问题,进行“有监督的预训练”,得到具有相同类型的输入特征的神经网络。
- 微调(fine tuning):然后借用上述神经网络,仅需更改其输出层,再按照当前任务的数据集继续训练。若当前任务的数据集较小,只需训练输出层参数;若当前任务的数据集较大,可以考虑重新训练全部参数。
注1:输入特征必须相同。比如用一个语音预训练的神经网络,就不能很好的迁移到图像分类问题。
注2:此技术不一定在每个场景都适用。
??注意到很多机器学习社区中,都有很多别人训练好的神经网络,所以“迁移学习”可以直接“站在巨人的肩膀上”.比如GPT3、GPT4、BERTs、在ImageNet上预训练的神经网络等,这些都是其他人在大型图像数据集或文本数据集上训练过的神经网络,可以在其他场景下微调。“迁移学习”的魅力在于共享,也就是开源精神,所有人的工作加起来肯定比一个人走得更远。
3.5 机器学习项目的完整周期
【问题1】“语音搜索”:用户语音输入想要搜索的内容,系统解析完毕后自动进行Web搜索。
- 输入特征:用户输入的音频。
- 输出:用户想要搜索的关键字。
??本小节来介绍构建机器学习项目的完整周期,以上面的“【问题1】语音搜索”举例:
- 确定项目范围:决定项目的目标及适用范围。比如“语音搜索”就只关心“语音输入”,而不关心“文字输入”。
- 收集数据:决定要收集哪些数据,用于训练机器学习系统。比如“语音搜索”中就可以收集大量的带标注的音频数据。
- 训练模型:训练模型并进行误差分析,不断迭代。误差分析的结果可能会提示我们收集更多的数据,比如“语音搜索”中,很多训练错误的样本都有汽车的背景噪音,那么就可以专门去搜集更多这类数据。
- 部署使用:模型训练的足够好后,就可以部署到生产环境中,供用户使用。部署后,还要持续监控并维护系统。这个过程中,源源不断出现的新数据将进一步有利于系统性能提升。若系统性能出现不可维护的下降,就需要回到上一步重新训练。

??在前面几小节的介绍中,我们对于前三步基本上有所了解,现在来着重介绍第四步“部署”。若神经网络的性能很强,则通常意味着该神经网络的规模很大,所以一种常见的部署模型的方法就是,将模型部署在服务器上,这个服务器被称为“推理服务器(inference server)”,该服务器的工作就是调用模型,并作出相应的预测。用户端则使用一个已经开发好的APP,这个APP就可以将用于的语音输入片段传递给“推理服务器”,然后“推理服务器”会返回一个结果给APP,进而由APP完成后续的工作。显然,在“部署”后,还要进行“运维”保证系统的正常工作,此时就需要考虑一系列“软件工程”:
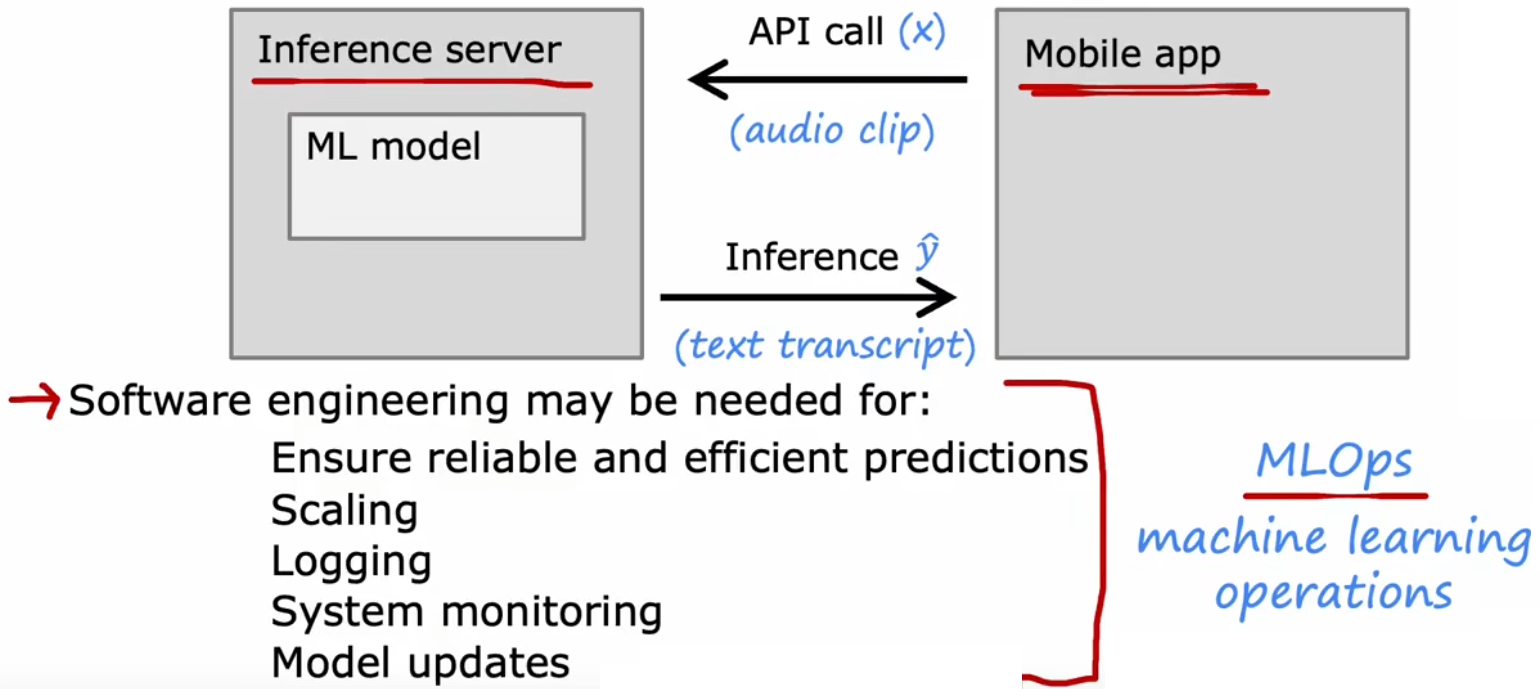
“部署”后的软件工程:
- 确保预测准确:也就是在尽可能减少计算成本的前提下,保证预测结果的准确。
- 大量的用户:有时当用户数量激增,软件工程需要确保系统工作正常。
- 记录日志:如果用户允许的话,可以记录每次的输入和输出。
- 系统监控:用户使用APP的过程中产生的数据,是监控整个系统很好的数据。若系统出现某方面的性能表现不佳,也可以及时进行下一步调整。比如突然出现某个热门事件或人物,此时旧的“语音搜索”模型的数据库并不包含此信息,就需要及时更新模型。
- 更新模型:对模型进行改进后,使用此新模型来替代服务器上的旧模型。
- ……
现在有一门新的领域叫做“机器学习操作(MLOps)”,旨在如何系统性地构建、部署、维护机器学习系统,以保证机器学习系统是可靠的、可扩展的、法律允许的、可监控的、可更新的等,来保证系统运行良好。比如,对于一个部署给几百万人使用的模型,如何进行高度优化来保证预测结果准确的前提下,尽可能减小计算成本。显然,机器学习服务的人数越多、任务越复杂,所需要考虑的“软件工程”就越多、配置人数就越多。
3.6 伦理道德规范
??最后一节来讨论一下伦理道德规范。在构建一个会影响人们的系统时,应该确保该系统绝对公平、没有偏见,并且不违反法律和道德的底线。比如下面就是一些反面的案例:
存在“偏见(bias)”的系统:
- 找工作的软件中,少分配或不分配女性应聘者。
- 警方的“面部识别”系统中,针对黑人面庞进行更加频繁的比对,以判断是否为“犯罪库”中的人脸。
- 银行的“贷款审批”系统中,刻意忽略某个子群体。
- 在进行“职业搜索”中,系统会暗示某个职业不好,比如“打死不学土木😂”,这会加重负面的刻板印象。
“不良使用(adverse use)”机器学习的系统:
- AI换脸。比如为了某些的政治目的,生成某些政治人物的AI换脸视频。
- 推送煽动性言论。比如一直推送特定的政治言论给某些特定群体。
- 刷评论。出于某种政治目的,使用机器学习自动在某些极端言论下刷好评。
- 欺诈。利用大数据对某人实施精准诈骗。这是一场反诈人员和诈骗人员的拉锯战。
??技术无罪,但使用技术的人可能有,所以不要做对社会产生危害的项目。虽然不同机器学习系统所需要考虑的伦理程度不同,比如“咖啡豆烘焙”要考虑的伦理问题就比“贷款审批”少得多,但老师希望所有机器学习领域的人都会一直讨论这些问题,可以在出现更大的错误之前提早避免。下面是一些可能的建议,以确保项目中更少偏见、更公平、更合乎道德:
- 组建多元化团队。这里的多元化包括很多特征,比如性别、种族、文化等。多元化团队实际上可以更好的集思广益进行开发,并且也可以规避可能的歧视错误。
- 寻找行业标准。比如在金融行业,已经开始制定标准,来定义什么是公平合理、没有偏见。
- 自我审查系统。在部署前,再次进行一次审查,以消除可能的偏见。
- 制定缓解计划。部署后,持续监控可能出现的不利影响,一旦出现迅速响应,比如回退到之前没有偏见的版本。在“自动驾驶”算法中,就会预先考虑到出现车祸后如何进行“缓解计划”,如沃尔沃的自动报警。
本节 Quiz:
Which of these is a way to do error analysis?
× Calculating the test error J t e s t J_{test} Jtest?.
× Collecting additional training data in order to help the algorithm do better.
× Calculating the training error J t r a i n J_{train} Jtrain?.(只算一个没啥用)
√ Manually examine a sample of the training examples that the model misclassified in order to identifty common traits and trends.We sometimes take an existing training example and modify it (for example, by rotating an image slightly) to create a new example with the same label. What is this process called?
√ Data augmentation
× Machine learning diagnostic
× Bias/variance analysis
× Error analysisWhat are two possible ways to perform transfer learning? Hint: two of the four choices are correct.
√ You can choose to train all parameters of the model, including the output layers, as well as the earlier layers.
× Given a dataset, pre-train and then further fine tune a neural network on the same dataset.
√ You can choose to train just the output layers’ parameters and leave the other parameters of the model fixed.
× Download a pre trained model and use it for prediction without modifying or re-training it.
4. 处理倾斜数据集(可选)
对于倾斜数据集,前面所学的误差衡量指标不再使用,本节就来介绍针对“倾斜数据集”的误差衡量指标。
4.1 倾斜数据集的误差指标
??若数据集中的正向样本和反向样本的比例严重失衡,就称这个数据集为“倾斜数据集(skewed datasets)”。使用“倾斜数据集”训练的模型,一般不能使用通常的错误指标来进行衡量,比如前面的“训练误差”、“验证误差”、“测试误差”。
现在举个🌰,假如某该罕见病在人群中只有0.5%的发病率(倾斜数据集),现在需要开发识别病人是否具有罕见病的神经网络分类器。若分类器对于“测试集”的“测试误差(预测错误的样本占比)”仅为1%,这看起来很好。但是,由于发病率只有0.5%,这个分类器显然并不能很好的完成工作。毕竟,就算把所有的输入样本都判定为没有罕见病,其“测试误差”都能达到更低的0.5%。
所以对于“倾斜数据集”,就需要使用不同的误差指标,一对常见的误差指标是使用“混淆矩阵(confusion matrix)”计算的“准确率(precision)”和“召回率(recall)”:

- True Positive(真阳性):实际为1,预测为1。预测正确。
- False Positive(假阳性):实际为0,预测为1。预测错误。
- False Negative(假阴性):实际为1,预测为0。预测错误。
- True Negative(真阴性):实际为0,预测为0。预测正确。
注:假设少数分类为1,也就是将“有罕见病”设置为1。
注:“准确率”针对预测本身,衡量是否准确;“召回率”针对全体样本,衡量能否找出全部阳性。
对于“倾斜数据集”,当算法的“准确率”、“召回率”都很高时,就可以说明算法有效。
4.2 准确率与召回率的权衡
??理想情况下,我们会希望“准确率”和“召回率”都很高。但实际上,会有这两者之间的权衡(trade-off)。这是由于在分类问题中,我们通常会在最后输出一个0~1之间的数字(如Sigmoid函数),然后设定一个阈值,来判断正负:
- 不能冤枉一个好人:提升阈值,准确率上升,召回率下降。
- 宁可错杀也不放过:降低阈值,准确率下降,召回率上升。
如果想同时考虑两个指标,方便自动调整阈值,可以使用“F1 score”。“F1 score”是“准确率”和“召回率”的调和平均数,越大越好:
Harmonic?Mean?of ?? P & R : F1?score = 1 1 2 ( 1 P + 1 R ) = 2 P R P + R \text{Harmonic Mean of}\; P \& R:\quad \text{F1 score} = \frac{1}{\frac{1}{2}(\frac{1}{P}+\frac{1}{R})} = 2\frac{PR}{P+R} Harmonic?Mean?ofP&R:F1?score=21?(P1?+R1?)1?=2P+RPR?
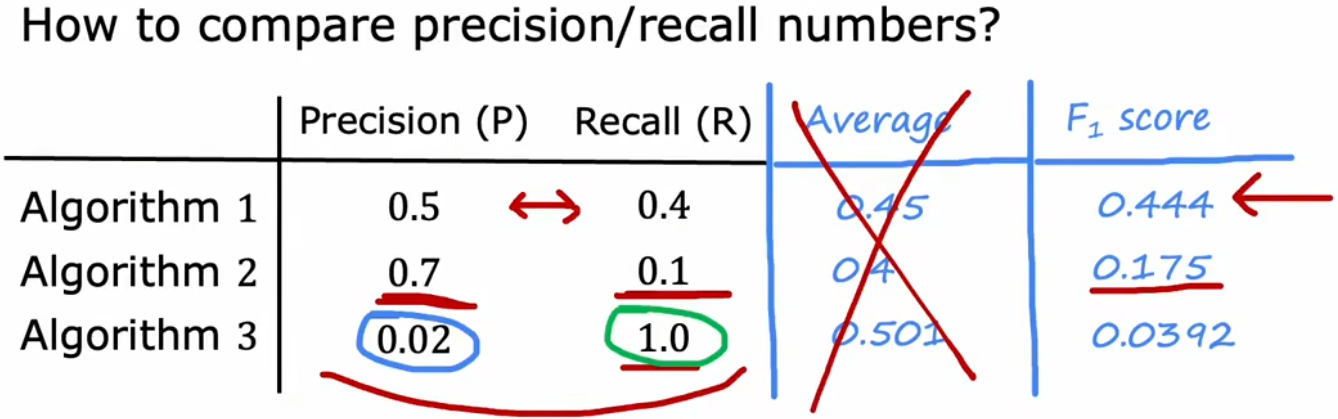
注:“调和平均”等价于并联电阻,任何一个指标特别小都会严重拖垮整体指标。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!
