支持向量机 支持向量机概述

2023-12-20 02:28:13

支持向量机概述

支持向量机 Support Vector MachineSVM ) 是一类按监督学习 ( supervisedlearning)方式对数据进行二元分类的广义线性分类器 (generalized linear classifier) ，其决策边界是对学习样本求解的最大边距超亚面 (maximum-margin hyperplane)与逻辑回归和神经网终相比，支持向量机，在学习复杂的非线性方程时提供了一种更为清晰，更加强大的方式

在这里插入图片描述

硬间隔、软间隔和非线性 SVM

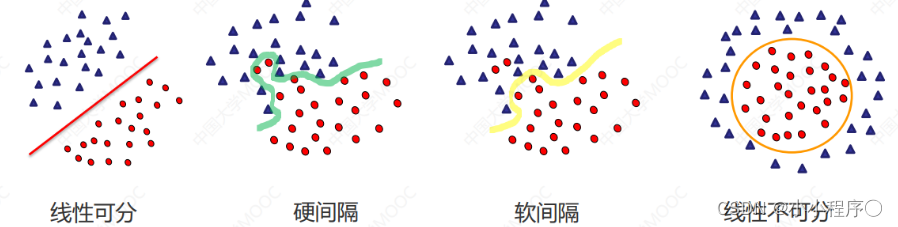
在这里插入图片描述

假如数据是完全的线性可分的，那么学习到的模型可以称为硬间隔支持向量机。换个说法，硬间隔指的就是完全分类准确，不能存在分类错误的情况。软间隔，就是允许一定量的样本分类错误。

算法思想

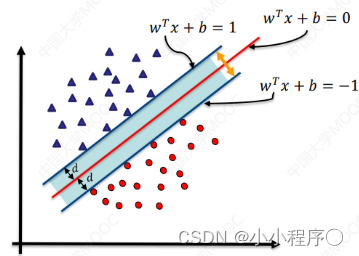
找到集合边缘上的若工数据 (称为支持向量 (Support Vector) )用这些点找出一个平面(称为决策面)，使得支持向量到该平面的距离最大
在这里插入图片描述

超平面方程：
w ? x + b = 0 \mathbf{w} \cdot \mathbf{x} + b = 0 w?x+b=0
间隔（Margin）：
Margin = 2 ∥ w ∥ \text{Margin} = \frac{2}{\|\mathbf{w}\|} Margin=∥w∥2?

决策函数：
( w ? x + b ) / ∣ ∣ w ∣ ∣ > = d , y = 1 (\mathbf{w} \cdot \mathbf{x} + b ) /||w|| >=d ,y=1 (w?x+b)/∣∣w∣∣>=d,y=1
( w ? x + b ) / ∣ ∣ w ∣ ∣ > = d , y = ? 1 (\mathbf{w} \cdot \mathbf{x} + b ) /||w|| >=d ,y=-1 (w?x+b)/∣∣w∣∣>=d,y=?1

如图所示，根据支持向量的定义我们知道，支持向量到超平面的距离为 d，其他点到超平面的距离大于 d

至此可以得到最大间隔超平面的上下两个超平面:
d = ∣ w ? x + b ∣ / ∣ ∣ w ∣ ∣ d=|\mathbf{w} \cdot \mathbf{x} + b | /||w|| d=∣w?x+b∣/∣∣w∣∣

文章来源:https://blog.csdn.net/2201_75381449/article/details/135095510
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。