Unity中Shader裁剪空间推导(正交相机到裁剪空间的转化矩阵)
文章目录
前言
我们把顶点坐标信息转化为裁剪空间。有可能使用到正交相机信息 或 透视相机。我们在这篇文章中,推导一下正交相机下的裁剪空间。
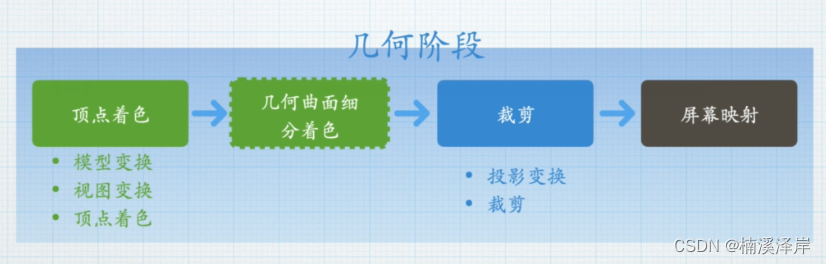
- 本地空间->世界空间->观察空间->裁剪空间->屏幕映射
一、正交相机 转化到 裁剪空间 干了什么
1、正交相机裁剪的范围主要是这个方盒子
- 因为使用的是右手坐标系。所以,摄像机的Z轴正方向是在X轴正方向右侧的。
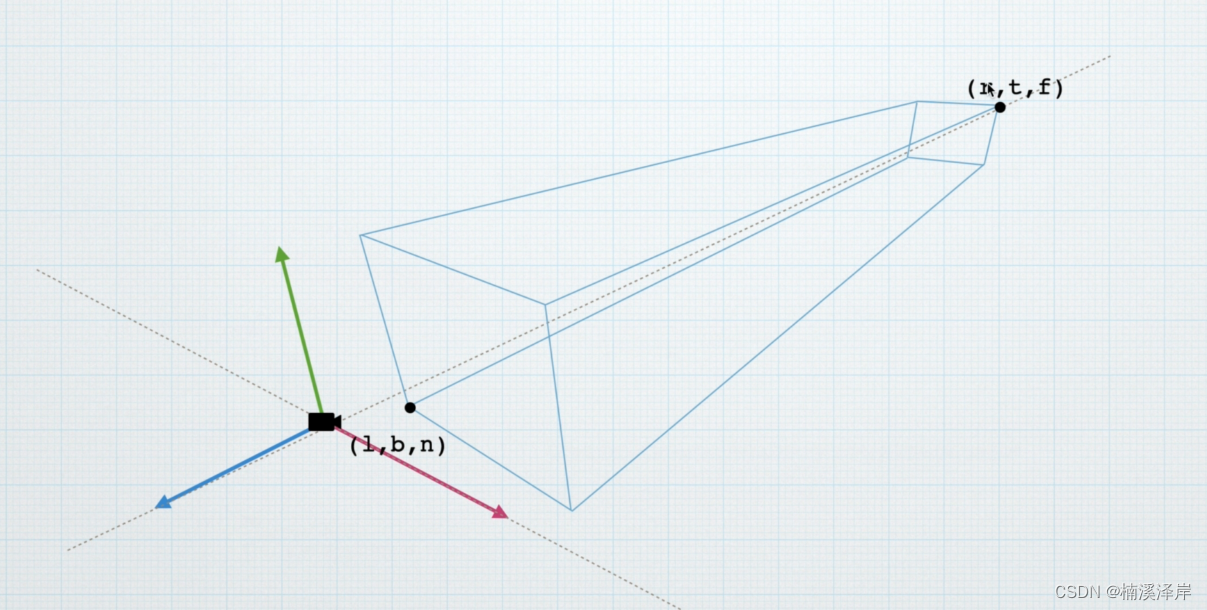
2、裁剪了之后,需要把裁剪范围内的坐标值化到[-1,1]之间,这就是我们的裁剪空间。
- 在不同平台下裁剪空间的X 和 Y轴范围都是[-1,1]
- OpenGL下,Z范围[-1,1]
- DirectX下,Z范围[0,1]
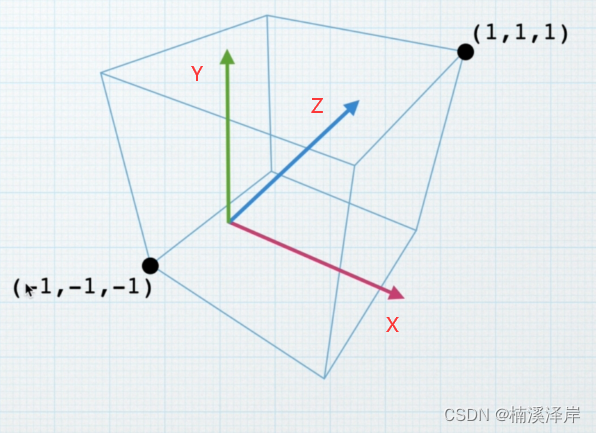
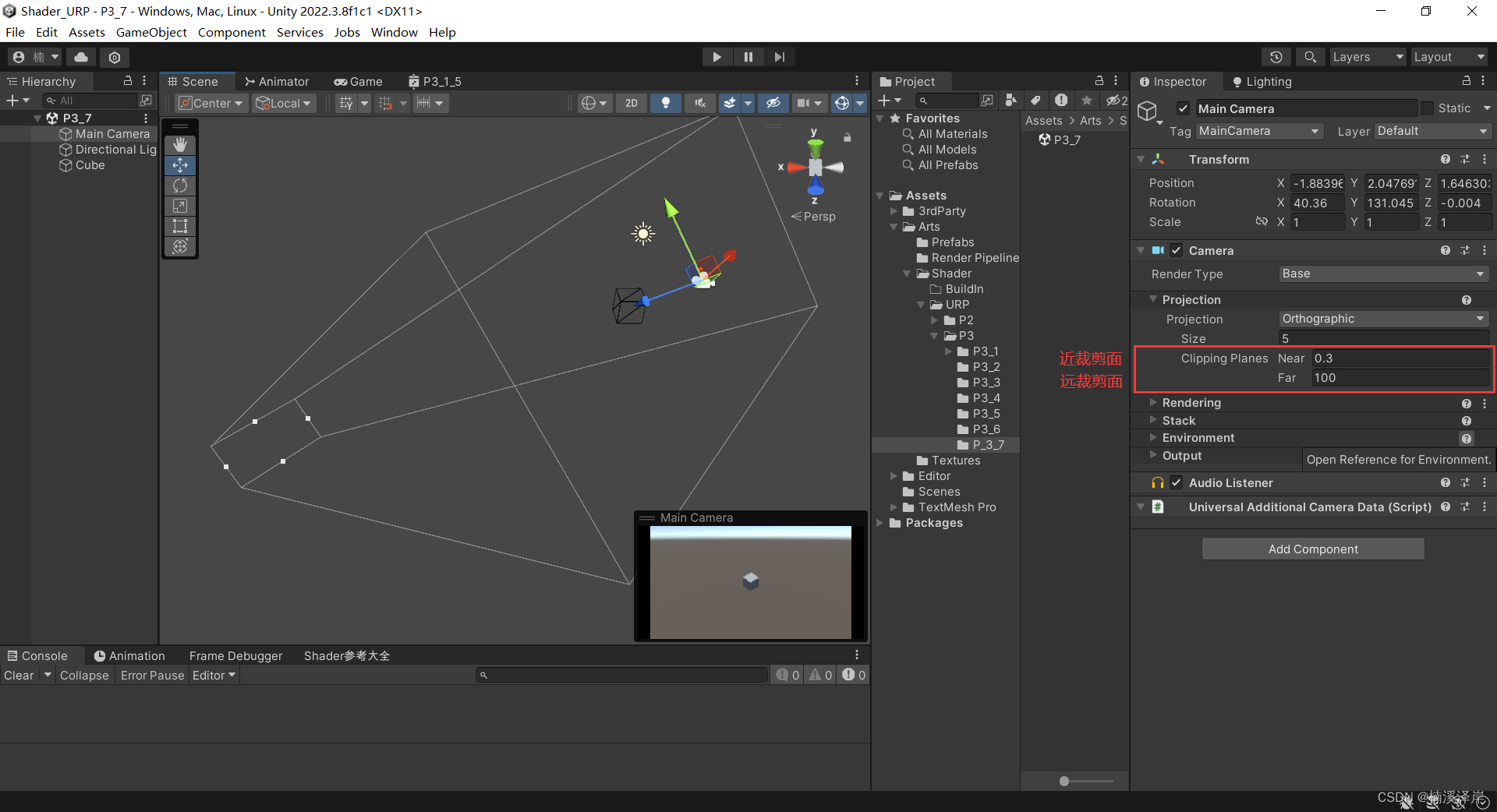
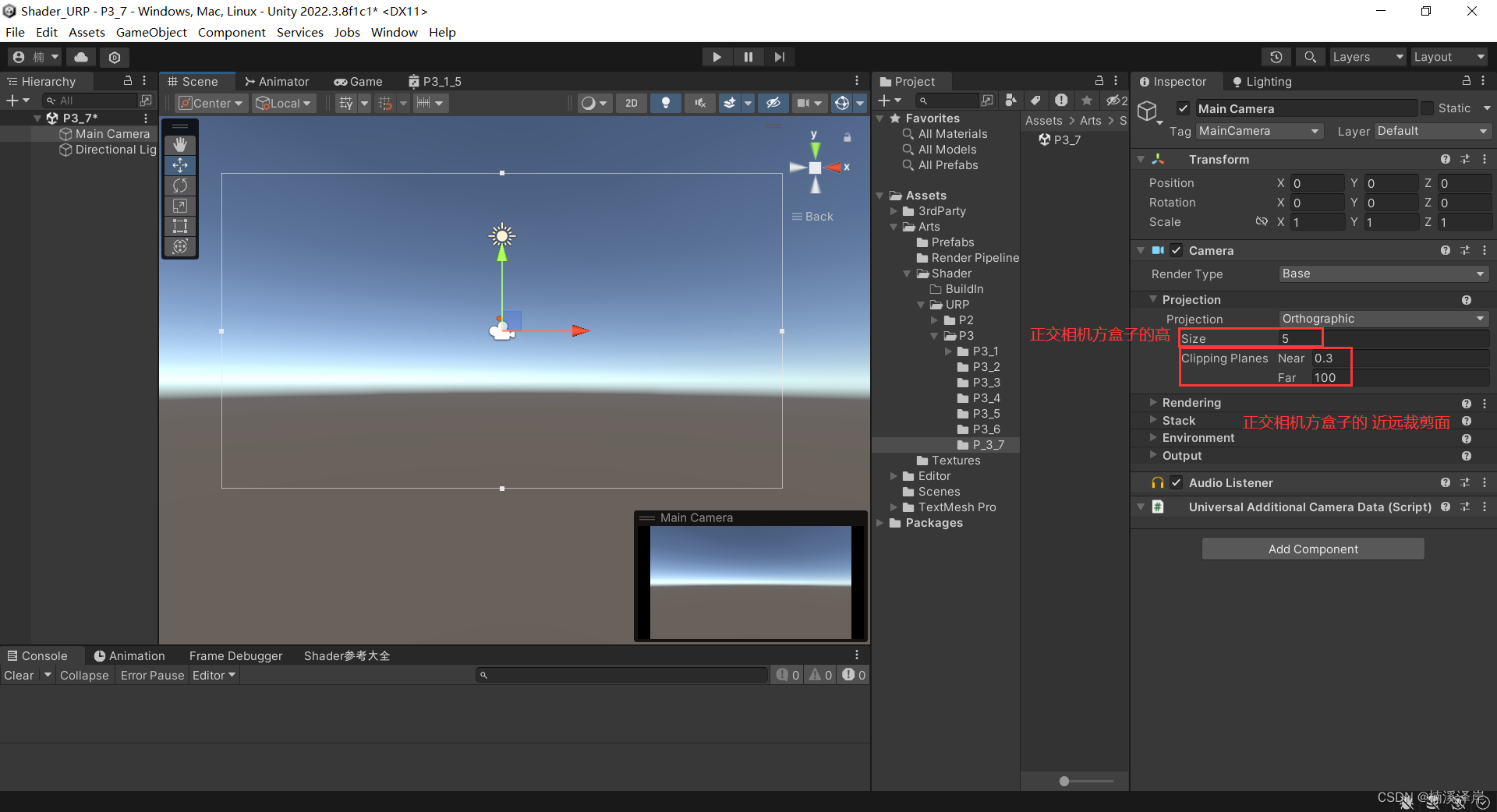
3、在Unity中,设置相机为正交相机
- Unity视图窗口使用了左手坐标系,Z轴正方向 在 X轴正方向左侧。但是,我们计算使用的是右手坐标系,这里需要注意。
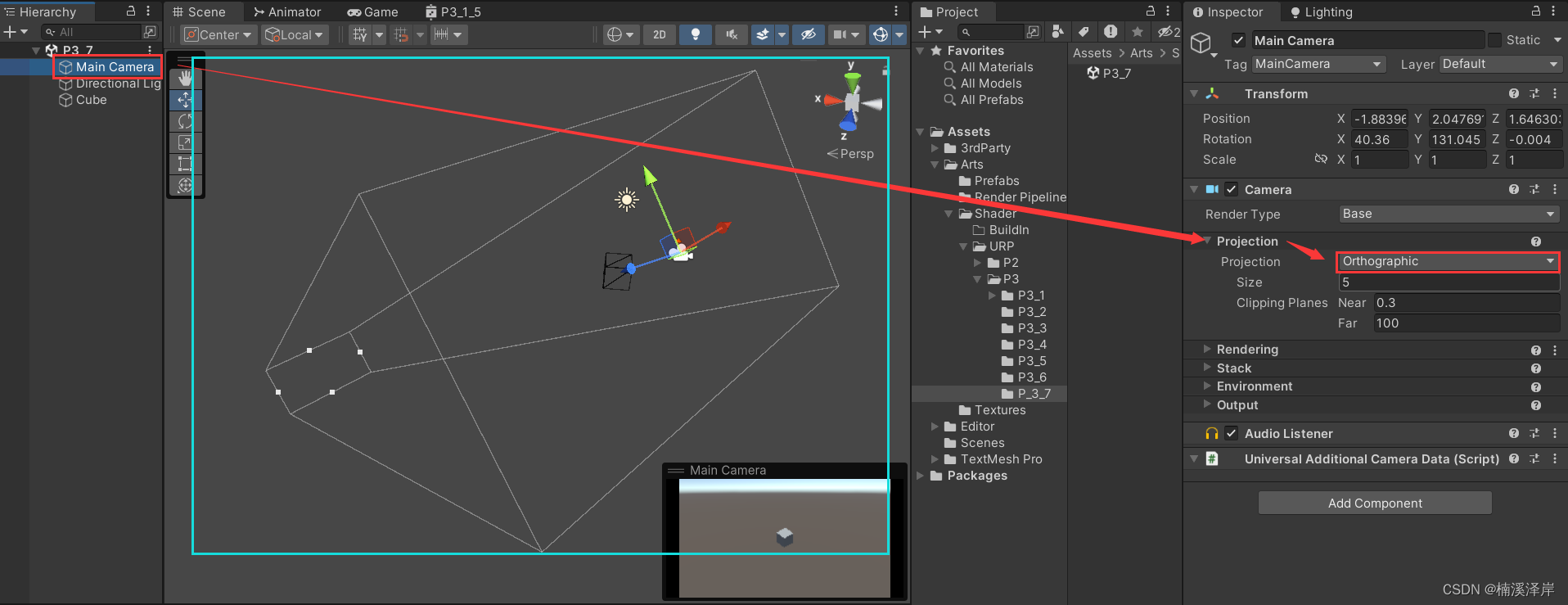
4、在这里设置相机的近裁剪面和远裁剪面
二、把正交相机的方盒子内的坐标 转化到 裁剪空间
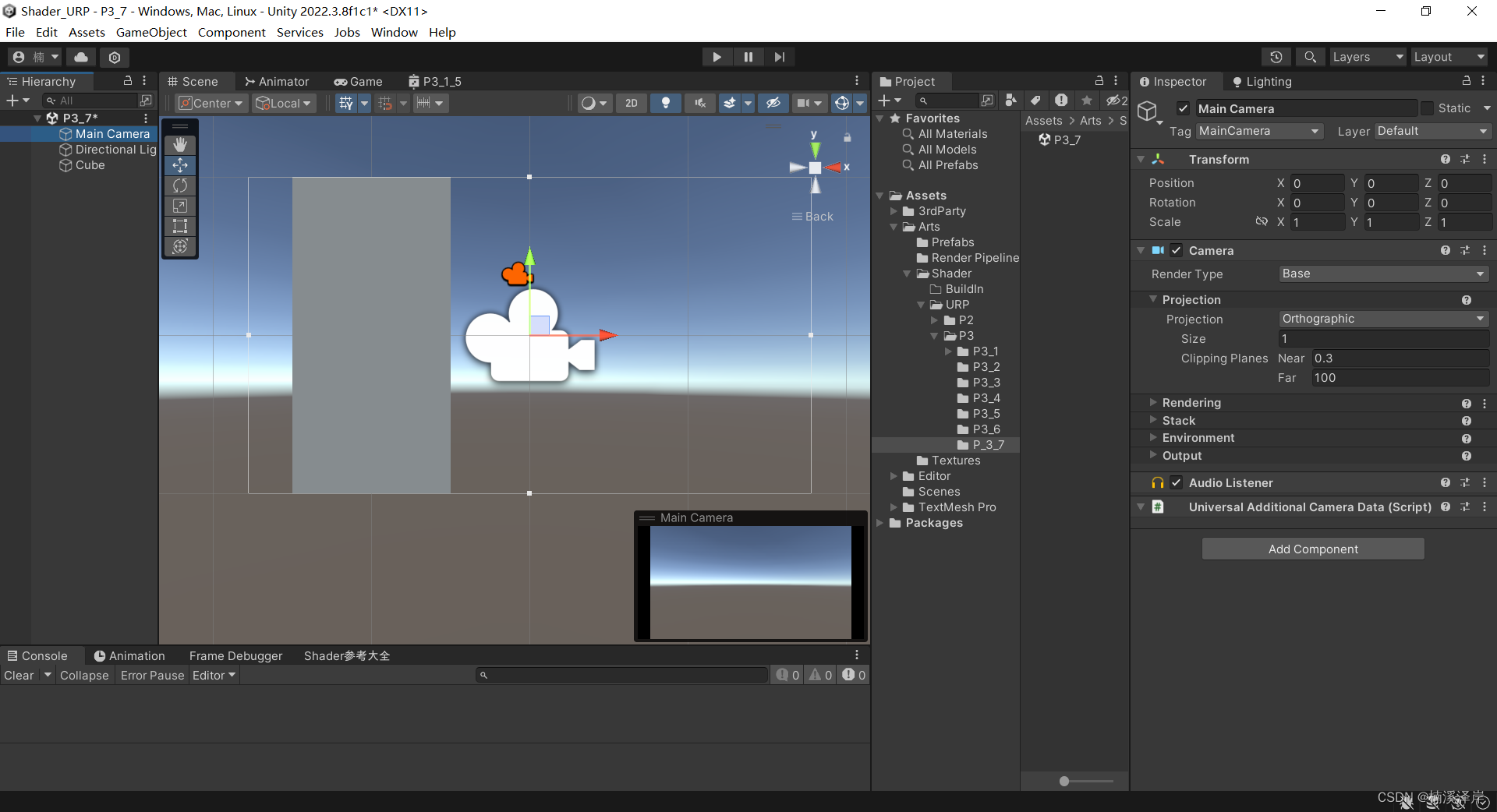
1、我们在Unity创建两个游戏对象来解释
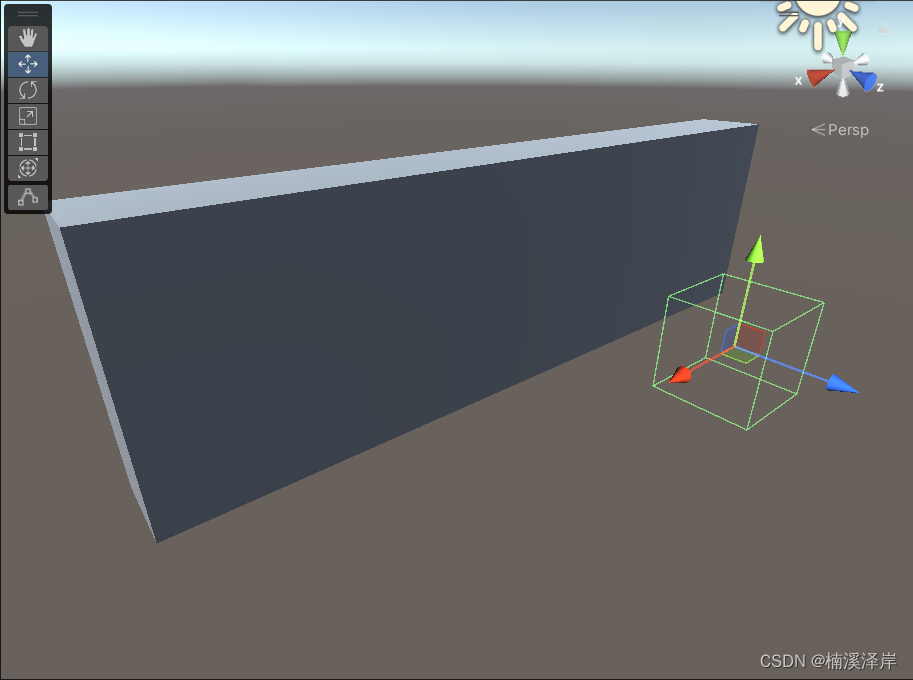
- 我们的绿线Cube相当于我们的裁剪空间
- 我们的大长方体相当于世界空间下的游戏对象
- 当我们进行转化时,对大长方体进行缩放、平移即可转化到裁剪空间
2、正交相机坐标 到 裁剪坐标 的映射关系
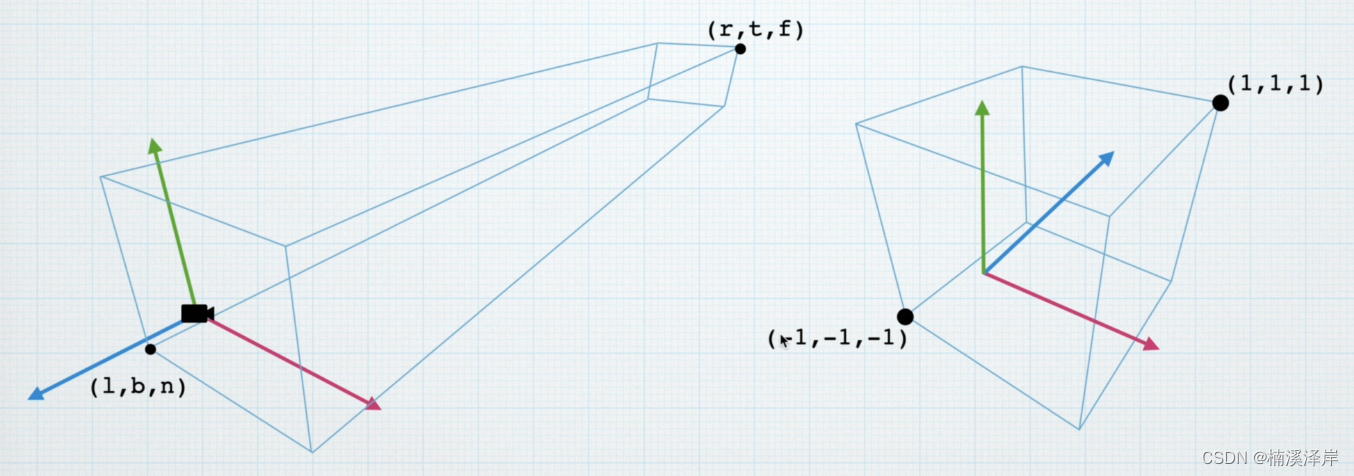
- l ≤ x ≤ r l \leq x \leq r l≤x≤r 化为 -1 ≤ x ≤ \leq x \leq ≤x≤ 1
- b ≤ y ≤ t b \leq y \leq t b≤y≤t 化为 -1 ≤ x ≤ \leq x \leq ≤x≤ 1
- f ≤ z ≤ n f\leq z \leq n f≤z≤n 化为 -1 ≤ x ≤ \leq x \leq ≤x≤ 1
3、化简X轴坐标
l ≤ x ≤ r l \leq x \leq r l≤x≤r
l ? l ≤ x ? l ≤ r ? l l - l \leq x - l \leq r - l l?l≤x?l≤r?l
0 ≤ x ? l ≤ r ? l 0 \leq x - l \leq r - l 0≤x?l≤r?l
0 ≤ x ? l 2 r ? l ≤ r ? l 2 r ? l 0 \leq x - l \frac{2}{r - l} \leq r - l \frac{2}{r - l} 0≤x?lr?l2?≤r?lr?l2?
0 ≤ 2 x ? 2 l r ? l ≤ 2 0 \leq \frac{2x - 2l }{r - l} \leq 2 0≤r?l2x?2l?≤2
? 1 ≤ 2 x ? 2 l r ? l ? 1 ≤ 1 -1 \leq \frac{2x - 2l }{r - l} - 1\leq 1 ?1≤r?l2x?2l??1≤1
? 1 ≤ 2 x ? 2 l r ? l ? r ? l r ? l ≤ 1 -1 \leq \frac{2x - 2l }{r - l} - \frac{r - l}{r - l}\leq 1 ?1≤r?l2x?2l??r?lr?l?≤1
? 1 ≤ 2 x ? l ? r r ? l ≤ 1 -1 \leq \frac{2x - l -r }{r - l} \leq 1 ?1≤r?l2x?l?r?≤1
-
l
=
?
r
,
r
=
?
l
l = -r,r = -l
l=?r,r=?l
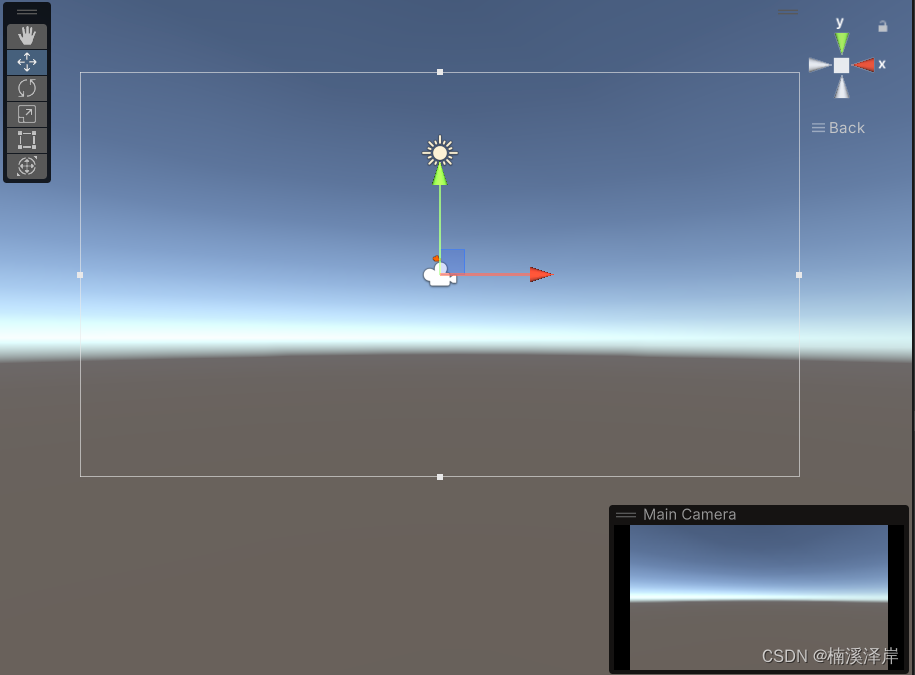
我们在Unity中看出,我们的正交相机是处于裁剪面中央的。
所以,我们的裁剪面x、y坐标,在摄像机空间下,是对称的。所以 r 和 l 是相反数。
? 1 ≤ 2 x ? ( ? r ) ? r r ? ( ? r ) ≤ 1 -1 \leq \frac{2x - (-r) -r }{r - (-r)} \leq 1 ?1≤r?(?r)2x?(?r)?r?≤1
? 1 ≤ 2 x 2 r ≤ 1 -1 \leq \frac{2x}{2r} \leq 1 ?1≤2r2x?≤1
- w = 2 l = 2 r w = 2l = 2r w=2l=2r
(w为我们正交相机方盒子的宽,这里在Unity中是未知的,我们这里先假设为w。后期可以化简为比值法从而不需要知道w的值)
我们已知的是:
正交相机方盒子的高 Size(等于Unity单位值的2倍)
正交相机的近远裁剪面(Z值)
? 1 ≤ 2 x w ≤ 1 -1 \leq \frac{2x}{w} \leq 1 ?1≤w2x?≤1
4、化简Y轴坐标
b ≤ y ≤ t b \leq y \leq t b≤y≤t
b ? b ≤ y ? b ≤ t ? b b - b\leq y - b \leq t - b b?b≤y?b≤t?b
0 ≤ y ? b ≤ t ? b 0\leq y - b \leq t - b 0≤y?b≤t?b
0 ≤ y ? b 2 t ? b ≤ t ? b 2 t ? b 0\leq y - b\frac{2}{t - b} \leq t - b\frac{2}{t - b} 0≤y?bt?b2?≤t?bt?b2?
0 ≤ 2 y ? 2 b t ? b ≤ 2 0\leq \frac{2y - 2b}{t - b} \leq 2 0≤t?b2y?2b?≤2
? 1 ≤ 2 y ? 2 b t ? b ? 1 ≤ 1 -1\leq \frac{2y - 2b}{t - b} - 1\leq 1 ?1≤t?b2y?2b??1≤1
? 1 ≤ 2 y ? 2 b t ? b ? t ? b t ? b ≤ 1 -1\leq \frac{2y - 2b}{t - b} - \frac{t - b}{t - b}\leq 1 ?1≤t?b2y?2b??t?bt?b?≤1
? 1 ≤ 2 y ? b ? t t ? b ≤ 1 -1\leq \frac{2y - b - t}{t - b}\leq 1 ?1≤t?b2y?b?t?≤1
-
b
=
?
t
,
b
=
?
t
b = -t,b = -t
b=?t,b=?t
我们在Unity中看出,我们的正交相机是处于裁剪面中央的。
所以,我们的裁剪面x、y坐标,在摄像机空间下,是对称的。所以 b 和 t 是相反数。

? 1 ≤ 2 y ? ( ? t ) ? t t ? ( ? t ) ≤ 1 -1\leq \frac{2y - (-t) - t}{t - (-t)}\leq 1 ?1≤t?(?t)2y?(?t)?t?≤1
? 1 ≤ 2 y + t ? t t + t ≤ 1 -1\leq \frac{2y + t - t}{t + t}\leq 1 ?1≤t+t2y+t?t?≤1
? 1 ≤ 2 y 2 t ≤ 1 -1\leq \frac{2y}{2t}\leq 1 ?1≤2t2y?≤1
- h = 2 b = 2 t h = 2b = 2t h=2b=2t
(h为我们正交相机方盒子的高,这里先假设h代替)
? 1 ≤ 2 y h ≤ 1 -1\leq \frac{2y}{h}\leq 1 ?1≤h2y?≤1
5、化简Z坐标(OpenGL下 [-1,1])

因为我们观察空间是右手坐标系。但是,我们裁剪空间是左手坐标系。所以,这里需要化简的式子需要变化一下。(左手坐标系Z轴正方向与上图相反)
- f ≤ z ≤ n f\leq z \leq n f≤z≤n 变为 ? n ≤ z ≤ ? f -n\leq z \leq -f ?n≤z≤?f
? n ≤ z ≤ ? f -n\leq z \leq -f ?n≤z≤?f
0 ≤ z + n ≤ n ? f 0\leq z + n \leq n-f 0≤z+n≤n?f
0 ≤ z + n 2 n ? f ≤ n ? f 2 n ? f 0\leq z + n \frac{2}{n - f} \leq n - f \frac{2}{n - f} 0≤z+nn?f2?≤n?fn?f2?
0 ≤ 2 z + 2 n n ? f ≤ 2 0\leq \frac{2z + 2n}{n - f} \leq 2 0≤n?f2z+2n?≤2
? 1 ≤ 2 z + 2 n n ? f ? n ? f n ? f ≤ 1 -1\leq \frac{2z + 2n}{n - f} - \frac{n-f}{n-f}\leq 1 ?1≤n?f2z+2n??n?fn?f?≤1
? 1 ≤ 2 z + n + f n ? f ≤ 1 -1\leq \frac{2z + n + f}{n - f} \leq 1 ?1≤n?f2z+n+f?≤1
? 1 ≤ 2 z + n + f n ? f ≤ 1 -1\leq \frac{2z + n + f}{n - f} \leq 1 ?1≤n?f2z+n+f?≤1
- 化简为线性式,方便后面把式子化为矩阵
? 1 ≤ 2 z n ? f + n + f n ? f ≤ 1 -1\leq \frac{2z}{n - f} + \frac{n+f}{n-f} \leq 1 ?1≤n?f2z?+n?fn+f?≤1
6、化简Z坐标(DirectX下 [0,1])

因为我们观察空间是右手坐标系。但是,我们裁剪空间是左手坐标系。所以,这里需要化简的式子需要变化一下。(左手坐标系Z轴正方向与上图相反)
- f ≤ z ≤ n f\leq z \leq n f≤z≤n 变为 ? n ≤ z ≤ ? f -n\leq z \leq -f ?n≤z≤?f
? n ≤ z ≤ ? f -n \leq z \leq -f ?n≤z≤?f
0 ≤ z + n ≤ n ? f 0 \leq z + n\leq n -f 0≤z+n≤n?f
0 ≤ z + n 1 n ? f ≤ 1 0 \leq z+n \frac{1}{n-f} \leq 1 0≤z+nn?f1?≤1
0 ≤ z + n n ? f ≤ 1 0 \leq \frac{z+n }{n-f} \leq 1 0≤n?fz+n?≤1
- 化简为线性式,方便后面把式子化为矩阵
0 ≤ z n ? f + n n ? f ≤ 1 0 \leq \frac{z}{n-f} + \frac{n}{n-f}\leq 1 0≤n?fz?+n?fn?≤1
三、把转化后的坐标转化为矩阵
-
X
? 1 ≤ 2 x w ≤ 1 -1 \leq \frac{2x}{w} \leq 1 ?1≤w2x?≤1 -
Y
? 1 ≤ 2 y h ≤ 1 -1\leq \frac{2y}{h}\leq 1 ?1≤h2y?≤1 -
Z(OpenGL)
? 1 ≤ 2 z n ? f + n + f n ? f ≤ 1 -1\leq \frac{2z}{n - f} + \frac{n+f}{n-f} \leq 1 ?1≤n?f2z?+n?fn+f?≤1 -
Z(DirectX)
0 ≤ z n ? f + n n ? f ≤ 1 0 \leq \frac{z}{n-f} + \frac{n}{n-f}\leq 1 0≤n?fz?+n?fn?≤1
1、OpenGL下
[ 2 w 0 0 0 0 2 h 0 0 0 0 2 n ? f n + f n ? f 0 0 0 1 ] \begin{bmatrix} \frac{2}{w} & 0 & 0 & 0 \\ 0 & \frac{2}{h} & 0 &0\\ 0 & 0 & \frac{2}{n -f} &\frac{n + f}{n - f}\\ 0 & 0 & 0 & 1\\ \end{bmatrix} ?w2?000?0h2?00?00n?f2?0?00n?fn+f?1? ?
2、DirectX
[ 2 w 0 0 0 0 2 h 0 0 0 0 1 n ? f n n ? f 0 0 0 1 ] \begin{bmatrix} \frac{2}{w} & 0 & 0 & 0 \\ 0 & \frac{2}{h} & 0 &0\\ 0 & 0 & \frac{1}{n -f} &\frac{n}{n - f}\\ 0 & 0 & 0 & 1\\ \end{bmatrix} ?w2?000?0h2?00?00n?f1?0?00n?fn?1? ?
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:veading@qq.com进行投诉反馈,一经查实,立即删除!