【数据结构(十·树结构的实际应用)】赫夫曼树（2）

---

1. 基本介绍

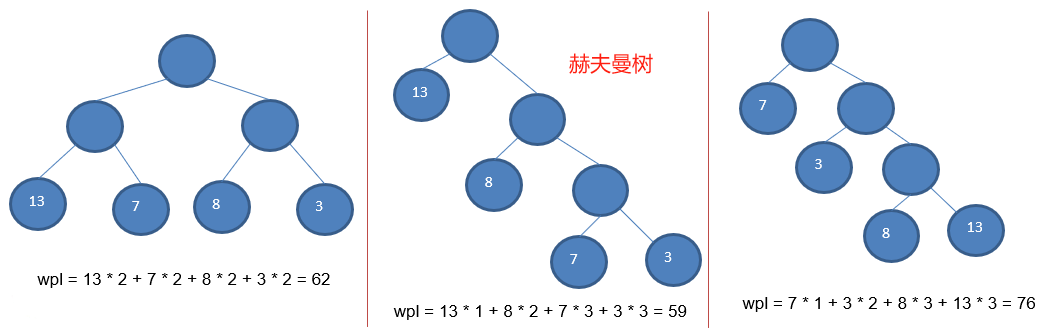
1. 给定 n 个权值作为 n 个叶子结点，构造一棵二叉树，若该树的 带权路径长度(wpl) 达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree), 还有的书翻译为霍（赫）夫曼树。
2. 赫夫曼树是带权路径长度最短的树，权值较大的结点离根较近。

几个重要的概念：
????① 路径和路径长度：在一棵树中，从一个结点往下可以达到的孩子或孙子结点之间的通路，称为路径。通路中分支的数目称为路径长度。若规定根结点的层数为 1，则从根结点到第 L 层结点的路径长度为 L-1。
????② 结点的权及带权路径长度：若将树中结点赋给一个有着某种含义的数值，则这个数值称为该结点的权。结点的带权路径长度为：从根结点到该结点之间的路径长度与该结点的权的乘积。
????③ 树的带权路径长度：树的带权路径长度规定为所有叶子结点的带权路径长度之和，记为 WPL(weighted path length) ,权值越大的结点离根结点越近的二叉树才是最优二叉树。

WPL 最小的就是赫夫曼树
????

2. 赫夫曼树的创建

问题：
????给一个数列 {13, 7, 8, 3, 29, 6, 1}，要求转成一颗赫夫曼树.

2.1. 思路分析

????① 从小到大进行排序, 将每一个数据，每个数据都是一个节点 ， 每个节点可以看成是一颗最简单的二叉树
????② 取出根节点权值最小的两颗二叉树
????③ 组成一颗新的二叉树, 该新的二叉树的根节点的权值是前面两颗二叉树根节点权值的和
????④ 再将这颗新的二叉树，以根节点的权值大小 再次排序， 不断重复 1-2-3-4 的步骤，直到数列中，所有的数据都被处理，就得到一颗赫夫曼树

图解：

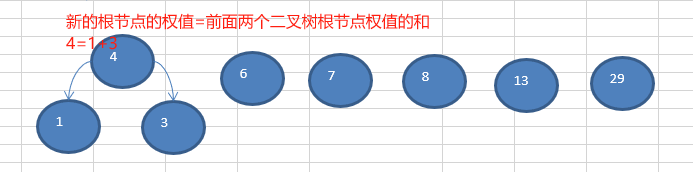
① 从小到大进行排序{1, 3, 6, 7, 8, 13, 29}, 将每一个数据，每个数据都是一个节点 ， 每个节点可以看成是一颗最简单的二叉树

② 取出根节点权值最小的两颗二叉树，即1和3

③ 组成一颗新的二叉树, 该新的二叉树的根节点的权值是前面两颗二叉树根节点权值的和(1+3=4)

④ 再将上面这颗新的二叉树，以根节点的权值大小 再次排序：取出上面 以根节点为4和6的二叉树，重复③步骤

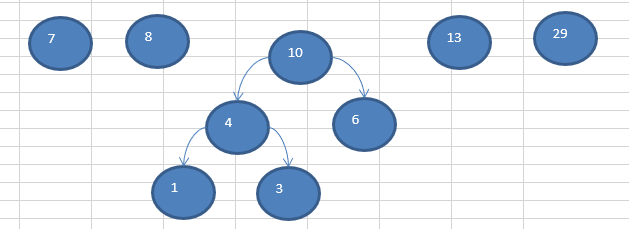
⑤ 不断重复上述操作，直到数列中，所有的数据都被处理，就得到一颗赫夫曼树
????（1）重复第一次

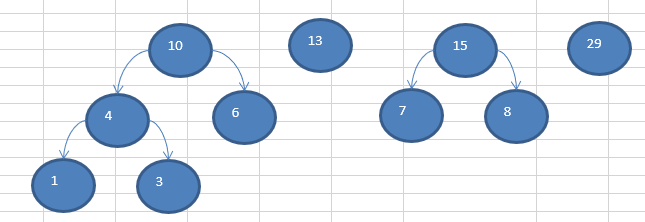
????（2）重复第二次

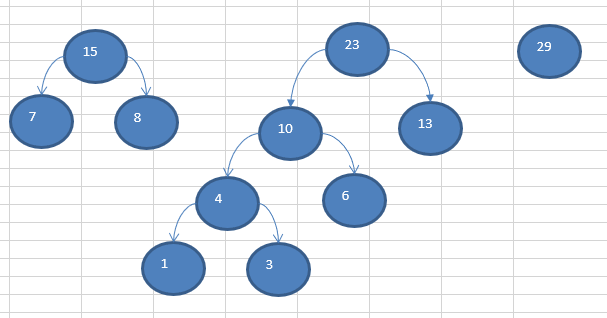
????（3）重复第三次

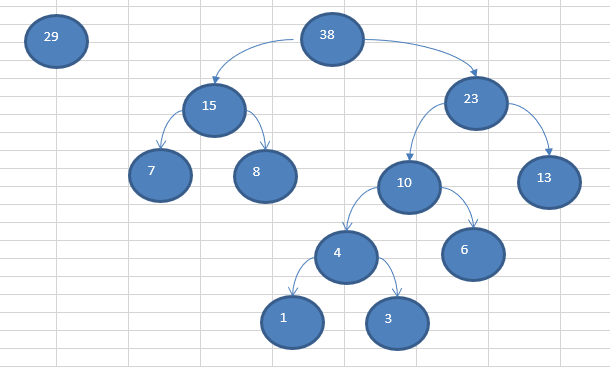
????（4）重复第四次（完成）

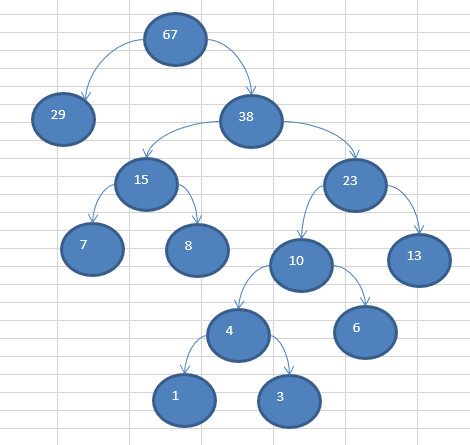
2.2. 代码实现

package huffmantree;

import java.util.ArrayList;
import java.util.Collections;
import java.util.List;

public class HuffmanTree {

	public static void main(String[] args) {
		// TODO Auto-generated method stub
		int arr[] = { 13, 7, 8, 3, 29, 6, 1 };

		Node root = createHuffmanTree(arr);

		// 测试
		preOrder(root);//

	}

	// 编写一个前序遍历的方法
	public static void preOrder(Node root) {
		if (root != null) {
			root.preOrder();
		} else {
			System.out.println("是空树，不能遍历~");
		}
	}

	// 创建赫夫曼树方法
	/**
	 * 
	 * @param arr 需要创建成赫夫曼树的数组
	 * @return 创建好后的赫夫曼树的root节点
	 */
	public static Node createHuffmanTree(int[] arr) {
		// 第一步：为了操作方便
		// 1. 遍历arr数组
		// 2. 将arr的每个元素构成一个Node
		// 3. 将Node放入到ArrayList中
		List<Node> nodes = new ArrayList<>();
		for (int value : arr) {
			nodes.add(new Node(value));
		}

		// 处理的过程是一个循环的过程
		while (nodes.size() > 1) {

			// 排序：从小到大
			Collections.sort(nodes);
			System.out.println("nodes = " + nodes);

			// 取出根节点权值最小的两个二叉树
			// 1. 取出权值最小的节点（二叉树）
			Node leftNode = nodes.get(0);
			// 2. 取出第二小的节点（二叉树）
			Node rightNode = nodes.get(1);

			// 3. 构建一个新的二叉树
			Node parent = new Node(leftNode.value + rightNode.value);
			parent.left = leftNode;
			parent.right = rightNode;

			// 4. 从ArrayList删除处理过的二叉树
			nodes.remove(leftNode);
			nodes.remove(rightNode);

			// 5. 将parent加入到nodes
			nodes.add(parent);
		}

		// 返回赫夫曼树的root节点
		return nodes.get(0);

	}

}

//创建节点类
//为了让Node对象持续排序Collections集合排序
//让Node实现Comparable接口
class Node implements Comparable<Node> {
	int value;// 节点权值
	Node left;// 指向左节点
	Node right;// 指向右节点

	// 写一个前序遍历
	public void preOrder() {
		System.out.println(this);
		if (this.left != null) {
			this.left.preOrder();
		}
		if (this.right != null) {
			this.right.preOrder();
		}
	}

	public Node(int value) {
		this.value = value;
	}

	@Override
	public String toString() {
		return "Node [value=" + value + "]";
	}

	@Override
	public int compareTo(Node o) {
		// TODO Auto-generated method stub
		// 表示从小到大排序
		return this.value - o.value;
	}

}

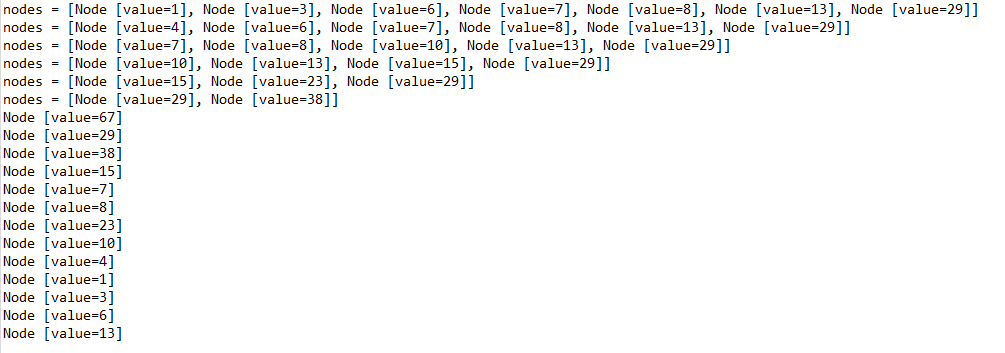
运行结果：