信息安全数学基础

定义1.1? 设a，b是任意两个整数，其中b！=0。如果存在一个整数q，使得等式

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?a=qb

成立，则称为b整除a或者a被b整除，记作b|a。? b叫做a的因数，a叫做b的倍数。

定理1.1 整除的传递性：设a！=0，b！=0，c是三个整数。若a|b，b|c，则a|c。

定理1.2 设a，b，c！=0是三个整数。若c|a，c|b，则c|a+b 或者 c|a-b。

定理1.3?设a，b，c！=0是三个整数。若c|a，c|b，则对于任意的整数s，t，有c|sa+tb。

定义1.2 设整数n！=0， $\pm$ 1，如果除了平凡因数 $\pm$ 1， $\pm$ n外，n没有其他因数，那么n叫做素数（或质数，不可约数）；否则n叫合数。

?定理1.4 （每个合数必有素因子）设n是一个正合数，p是一个n的大于1的最小正因数，则p一定是素数，且p<= $\sqrt{n}$ 。

厄拉托塞师筛法：寻找素数的确定性方法

步骤：1.找出<= $\sqrt{n}$ 的所有素数；?

? ? ? ? ? ?2.依次删除这些素数的倍数

? ? ? ? ? ?3.余下的数就是素数

定理1.5 素数有无穷多个?

欧几里得算法?

定理1.7 （Euclid除法，也称为带余除数）设a，b是两个整数，其中b>0,则存在唯一的整数q，r，使得

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? a=qb+r? ? 0 <= r < b

定义1.4? a=qb+r? ? 0 <= r < b? 其中q叫做a被b除所得的不完全商，r叫做a被b除所得的余数。

定义1.5 （公因子）设 a1，.......，an是n（n>=2）个整数。若整数d是他们中每一个数的因数，那么d叫做a1，.......，an的一个公约数（也叫公因数）。

d是a1，.......，an的一个公约数的数学表达式为? ? d|a1，......，d|an

如果整数a1，.......，an不全为0，那么a1，.......，an的所有公约数中最大的一个公约数叫做最大公约数，记作gcd（a1，......an）或a1，......an）。

特别的，当（a1，......an）=1，称(a1，......an）互素或者互质。

定理1.8 a，b是不全为0的整数，a，b的最大公约数d=（a，b）是集合?

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? {sa+tb|s，t $\epsilon$ Z}

中的最小整数。

定理1.10 设a1，......an是n个不全为0的整数，则

（1）a1，......，an与|a1|，......，|an|绝对值是相同的

（2）a1，......，an?=（|a1|，......，|an|）

定理1.11 设b是任意正整数，则（0，b）?

因为任何非零整数都是0的因数。

定理1.12 设a，b，r是三个不全为0的整数。如果

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?a=qb+r?

其中q是整数，（a，b）=（b，r）。

注：这条性质用于欧几里得除法求最大公因数。当c=0时，b为最大公因数。

可以求两个较大数的公因数转化为求两个较小数的公因数。

?例：

因为 1573=5*286+143,所以（1573,286）=（186,143）=143

扩展欧几里得除法

例题

计算 gcd（169,121）=1的分解步骤

169=1*121+48

121=2*48+25

48=1*25+23

25=1*23+2

23=11*2+1

2=2*1+0

?定理1.12 设a,b是任意两个正整数，则存在整数s,t，使得s*a+t*b=(a,b)。

（这个式子是最大公因式反过来求s,t）

将上述的例子反过来写

1=23-11*2

? =23-11*（25-1*23）

? =-11*25+12*23

? =-11*25+12*（48-1*25）

? =12*48-23*25

? =12*48-23*（121-2*48）

? =-23*121+58*48

? =-23*121+58*（169-1*121）

? =58*169-81*121

根据s*a+t*b=1,所以 s=58，t=-81.

算数基本定理

定理1.14? 设a，b是任意两个不全为零的整数：

（1）若m是任意正整数，则（am，bm）=（a，b）m

（2）若非零正整数d满足d|a，d|b，则（d/a,d/b）=(a,b )/d。特别的，有

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?(a/(a,b)),(b/(a,b))=1

定理1.15? 设a1，.......，an是n个整数，且a1 $\neq$ 0。令

? ? ? ? ? ? ? ? ?（a1，a2）=d2，（d2，a3）=d3，......，（dn-1，an）=dn。

则（a1，......an）=dn。

（多个整数的最大公因数）

?定理1.16? 设a，b，c是三个整数，b，c $\neq$ 0，如果（a，c）=1，则

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （ab，c）=（b，c）

?定理1.17? 设p是素数，p|ab，则 p|a 或者 p|b。

定理1.18?? 设a1，.......，an是n个整数。若（ai，c）=1,1 $\leqslant$ ?i? $\leqslant$ n，则

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（a1.......an，c）=1

定义1.6? （最小公倍数）设a1，.......，an是n个整数。若m是这n个数的倍数，则m叫做这个数的公倍数。a1，.......，an的所有的公倍数中的最小的正整数叫作最小公倍数，记作[a1，.......，an]。

m=[a1，.......，an]的数学描述：

（1）a1|m，.........，an|m。

（2）若a1|m'，........，an|m',则m|m'。

定理1.19? 设a，b是两个互素的整数，则

（1）若a|m，b|m，则ab|m。

（2）[a,b]=ab

定理1.20? ?设a，b是两个正整数，则

（1）a|m，b|m，则[a,b]|m

（2）[a,b]=ab/（a，b）

定理1.21? 设?a1，.......，an是n个整数，且a1 $\neq$ 0.令

? ? ? ? ? ? ?[a1,a2]=m2,[m2,a3]=m3,........,[mn-1,an]=mn

则? ? ? ? ? ? ? ? ? ? ? ? [a1,.........,an]=mn

算数基本定理：

定理1.22? 任何一个正数n>1都可以表示成素数的乘积，且在不考虑乘积顺序的情况下，该表达式是唯一的，即

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?n=p1.......ps,? ? ? ? ? ? p1 $\leqslant$ .... $\leqslant$ ps

其中pi是素数，且若

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?n=q1........qt,? ? ? ? ? ? q1 $\leqslant$ .... $\leqslant$ qt

其中qj是素数，则s=t? ，pi=qi

?例如：45=3*3*5? ?35=5*7等

?例题：

求解（45,100）和[45,100]

解答;? ? ?45= $2^{0}*3^{2}*5^{1}$

? ? ? ? ? ?100= $2^{2}*3^{0}*5^{2}$

所以? （45,100）= $2^{0}*3^{0}*5^{1}$ =5

? ? ? ? ? ? ?[45,100]? = $2^{2}*3^{2}*5^{2}$ =900

第二章同余

同余

定义2.1 给定一个正整数m，如果两个整数a，b有m|a-b，则a，b模m同余。

记作a $\equiv$ b（mod m）；否则，a，b模m不同余，记作a $\not\equiv$ b（mod m）。

定理2.1 设m是一个正整数，a，b是两个整数，则a $\equiv$ b（mod m）的充要条件是，存在一个整数k，使得a=b+km。

定理L1? 设m是一个正整数，则整数a，b模m同余的充分必要条件是a，b被m除的余数相同?。

定理2.2? （1）自反性对任意一个整数a，a $\equiv$ a（mod m）?

? ? ? ? ? ? ? （2）对称性若a $\equiv$ b（mod m），则b $\equiv$ a（mod m）

? ? ? ? ? ? ? （3）传递性若a $\equiv$ b（mod m），b $\equiv$ c（mod m），则?a $\equiv$ c（mod m）

定理2.3 设m是给定的一个正整数，a1，a2，b1，b2是四个整数，如果

?????????????????????????????????????????????????????????a1 $\equiv$ b1（mod m）

?????????????????????????????????????????????????????????a2 $\equiv$ b2（mod m）

则有

??????????????????????????????????????????????????????????a1 $\pm$ a2 $\equiv$ b1 $\pm$ b2?（mod m）

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??a1*a2 $\equiv$ b1*b2（mod m）

（1）前提是：若果是两个不同的多项式，则对应系数模m同余

（2）如果是未知数模m同余，则两个多项式模m同余

（3）如果对一个多项式 f(x)，对满足 x=y(mod m)的任意x，y，有：f(x)=f(y) (mod m)

例题

?定理L3? 若ac=bc (mod m)，(c,m)=d，则??a $\equiv$ b（mod m/d）

?定理2.4?设m是一个正整数，ad $\equiv$ bd（mod m），如果（d，m）=1，则

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ????a $\equiv$ b（mod m）

（该定理说明了同余关系的“消去”原则是消去值与模的互素）

?定理L4? 设??a $\equiv$ b（mod m），则（a，m）=（b，m）。

?剩余系

?例题

?定理2.7? 设m是正整数，则m个整数a1，a2，......，am为模m的一个完全剩余系的充要条件是他们模m两两不同余。

?定理2.8? 设m是正整数，整数a满足（a，m）=1，b是任意整数。若x遍历模m的一个完全剩余系，则ax+b也遍历模m的一个完全剩余系。

求逆元

?简化剩余系

注意是与m互质，而不是本身是素数。

?欧拉函数

注意：1与任何数都互素?

?欧拉定理

例题

费马定理?

Wilson定理?

第三章? 同余式

一次同余式

如果，整数a使得? ? f(a) $\equiv$ 0(mod m)? ?成立，则a叫做同余式的解。

注：是a叫做，不是f(a)叫做。

满足x $\equiv$ a(mod m)的所有整数都使得同余式成立。所以，以一个剩余类作为一个解。

在模m的完全剩余系中，使得同余式成立的剩余类的个数叫做同余式的解数。

只要找到一个整数a满足? f(a) $\equiv$ 0(mod m) ，那么凡是与a模m同余的整数都满足，但所有这些与a模m同余的整数职能算该同余式的一个解。

通常是遍历模m的最小非负完全剩余系。

通过这些例子可以知道，给定同余式的方程，方程解的情况可能是一个，或者多个。但多个解是有限的，最多只能有模m个。

?一次同余式求解

?注意：这一题因为（a，m）=1，所以存在唯一解。

?中国剩余定理（CRT）

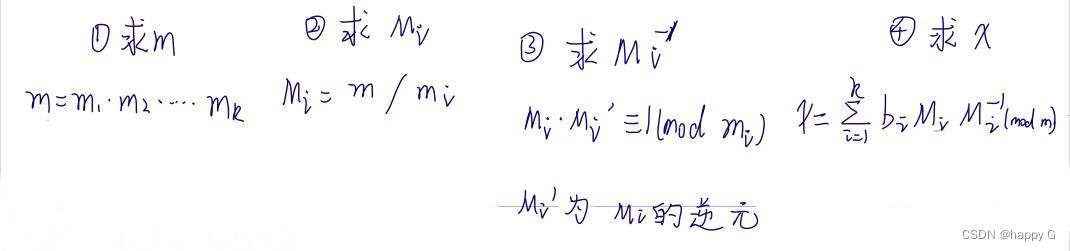
?模重复平方算法

?第四章二次同余式与平方剩余

二次同余式与平方剩余

注意：“a是否为模m的平方剩余”是通过“同余式 $x^{2}\equiv$ a（mod m）是否有解”来定义的。

在定义中需要注意以下三点：

（1）（a，m）=1，表示s是模m完全剩余系中的一个数。

（2）如果存在整数x满足 $x^{2}\equiv$ a（mod m），且（a，m）=1，则（x，m）=1。

（3）“平方剩余”是指a，并不是同余式的解。

?欧拉判定法则（奇素数）

?Legebdre符号（素数）

?

文章来源:https://blog.csdn.net/weixin_57472404/article/details/124479710
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：veading@qq.com进行投诉反馈，一经查实，立即删除！