浅谈倍增与ST表

如果我们有一个长度为 $n$ 的数组 $a$，现在有 $q$ 次询问，每次询问区间 $[l,r]$ 的最大值。应该怎么做？$(n,q\le 2\times 10^5)$

如果暴力，就是 $\Theta (n^2)$ 的，显然行不通。这时，就要用到ST表。

ST表是一种基于倍增思想的数据结构，支持对于一个数组无修改、区间修询问的大部分操作。接下来讲解一下他的运行过程。

Part 1：预处理ST表

设 $f[i][j]$ 表示 $a$ 数组区间 $[i,i+2^j)$ 的最大值。此时，我们可以运用类似DP的思想计算：

• 初始化：$?i\in [1,n],f[i][0]=a[i]$
• 运算顺序：优先从小到大枚举 $j$，$i$ 的枚举顺序任意。
• 状态转移方程：$f[i][j]=\max (f[i][j?1],f[i+2^{j?1}][j?1])$

此时，时间复杂度与空间复杂度均为 $\Theta (n\log n)$。

Part 2：求询问

这里就运用了倍增思想。对于一个询问区间 $[l,r]$，我们可以将他分成若干段，使得每段的长度都可以表示为 $2^i$，这样再利用数组 $f$ 就可以求出答案。

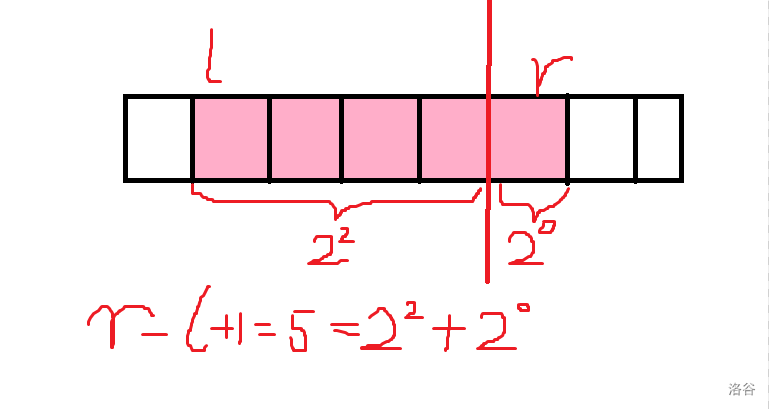
因此我们从大到小枚举 $i$：$(i\ge 0)$

• 如果 $r?l+1\le 2^i$，则 $ans=\max (ans,f[l][i])$，随后 $l\to l+2^i$。
• 否则什么也不做

最终我们能够得出答案。单次询问时间复杂度 $\Theta (\log n)$。

例题：

洛谷 P3865 【模板】ST 表
洛谷 P2251 质量检测

总结：倍增十分巧妙的运用了一个数可以分解为多个2的k次方数的特性，而ST表则是运用了倍增思想从而做到快速求解区间询问问题。